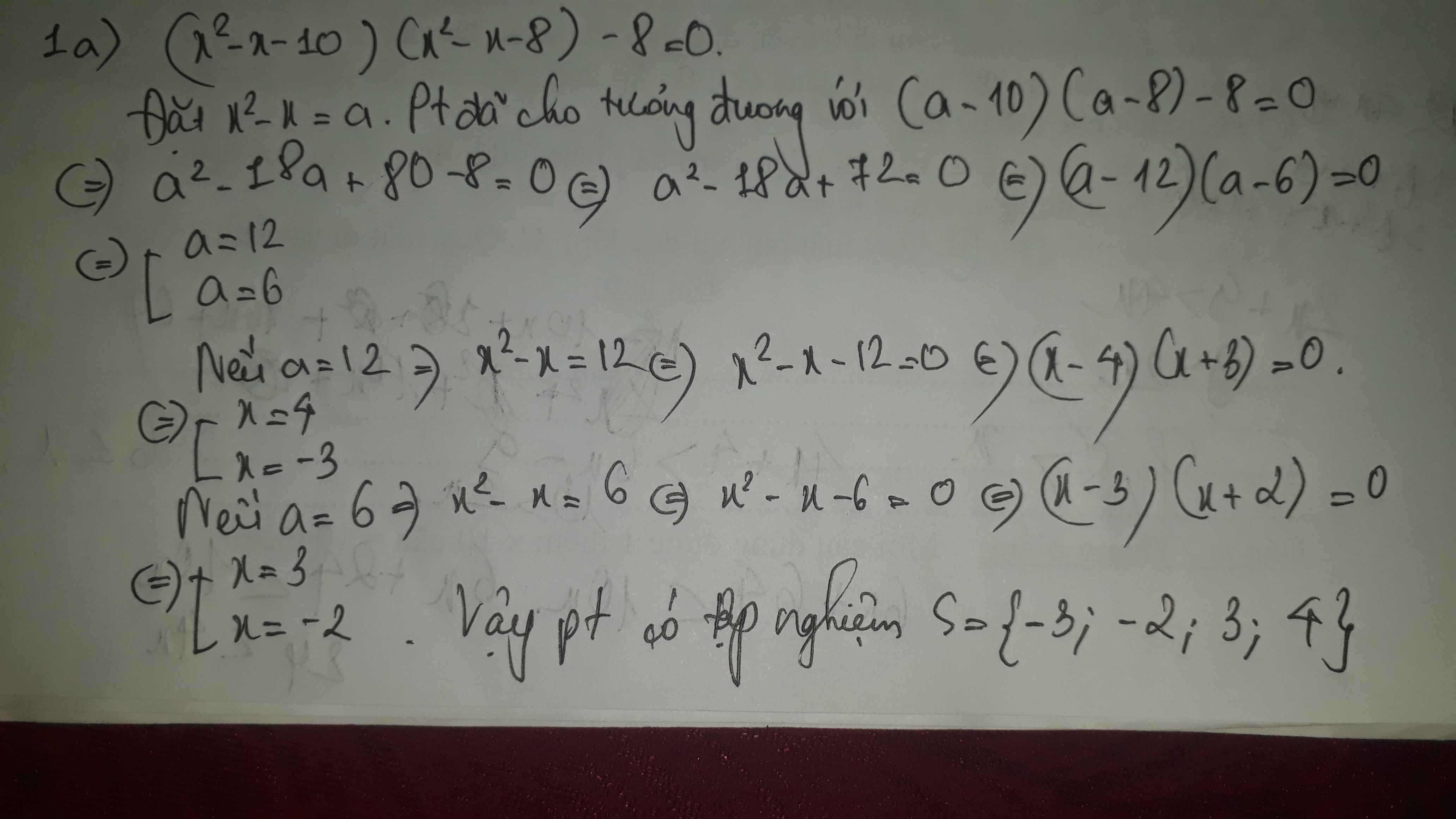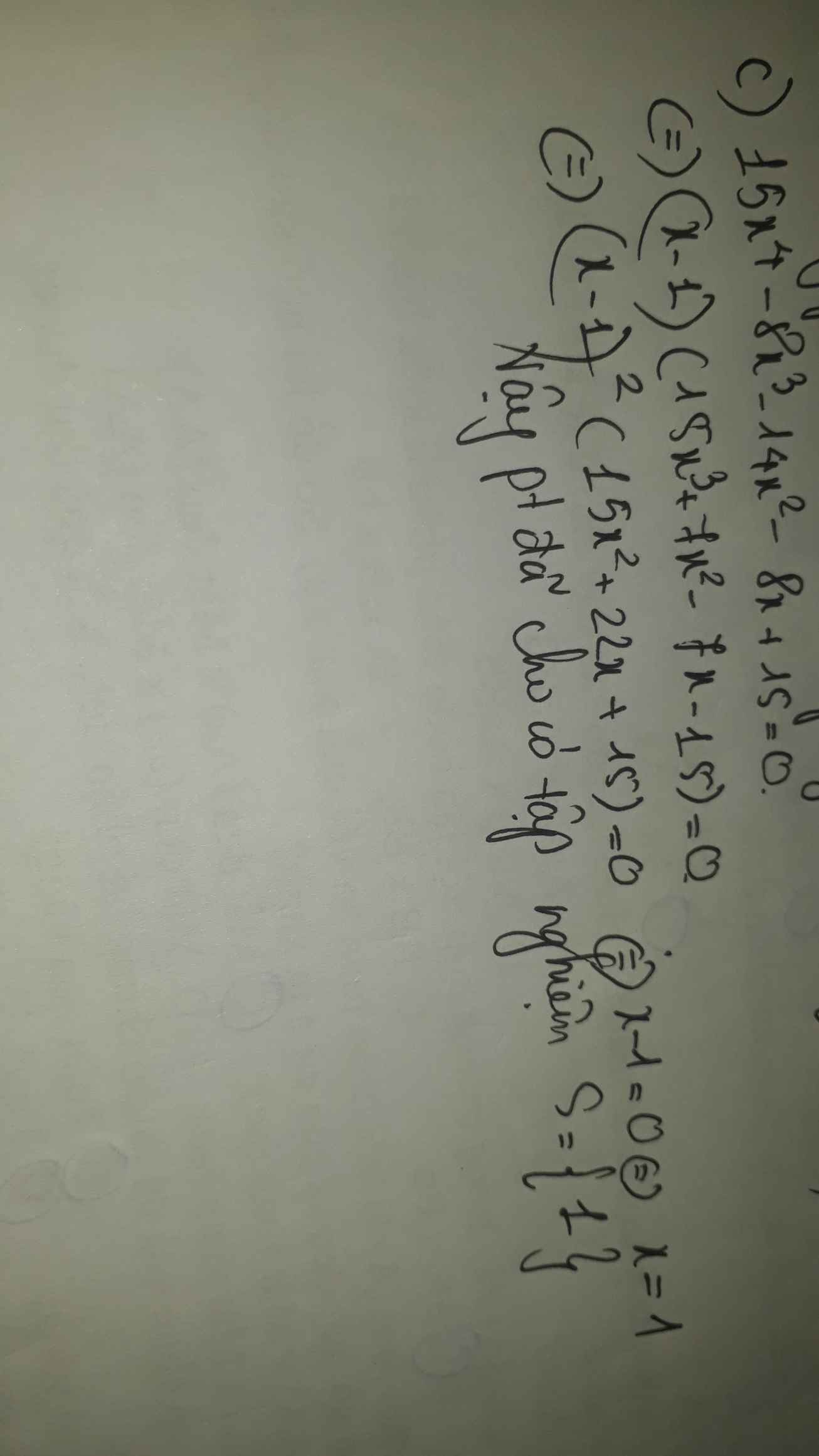Giải phương trình: 8x+15x=17x
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
giải hệ phương trình 17x - 10y = 48
15x - 25y = -96
GIẢI PHƯƠNG TRÌNH:
\(\sqrt{2x+1}+\sqrt{17-2x}=x^4-8x^3+17x^2-8x+22\)
TL
27 tháng 10 2021 lúc 20:59
giải phương trình nghiệm nguyên sau:
\(15x^2-7y^2=9\)
\(8x^3=3^y+997\)
giúp mình vs, mình cần trước thứ 6 nhé, mik cảm ơn nhiều
Đúng 0
Bình luận (0)
HM
28 tháng 5 2022 lúc 22:23
Giải phương trình:
\(\sqrt{13x^2-6x+10}+\sqrt{5x^2-13x+\dfrac{17}{2}}+\sqrt{17x^2-48x+36}=\dfrac{1}{2}\left(36x-8x^2-21\right)\)
Giải hệ phương trình sau
\(\hept{\begin{cases}y^2\sqrt{2x-1}+\sqrt{3}\\2y^4\left(5x^2-17x+6\right)=6-15x\end{cases}}=5y^2-\sqrt{6x-3}\)
1,giải các phương trình sau
a,(x^2-x-10).(x^2-x-8)-8=0
b,(x-1).(x+1).(x+3).(x+5)+15=0
c,15x^4-8x^3-14x^2-8x+15+0
Xem thêm câu trả lời
Giải phương trình:
\(3x^2-x+36=4\sqrt{6x^2-15x+27}+6\sqrt{2x^2+8x-6}\)
Giải phương trình:
\(\sqrt{x+x^2}+\sqrt{x-x^2}=x+1\)
\(\sqrt{2x+1}+\sqrt{17-2x}=x^{\text{4}}-8x^3+17x^2-8x+22\)
Bạn nào giải nhanh thì mình sẽ like nhé!
a đề sai hay sao mà vô nghiệm ?
b)Áp dụng BĐT Cauchy-Schwarz ta có:
\(VP^2=\left(\sqrt{2x+1}+\sqrt{17-2x}\right)^2\)
\(\le\left(1+1\right)\left(2x+1+17-2x\right)=36\)
\(\Rightarrow VP^2\le36\Rightarrow VP\le6\)
Lại có: \(VT=x^4-8x^3+17x^2-8x+22\)
\(=\left(x-4\right)^4+8\left(x-4\right)^3+17\left(x-4\right)^2+6\ge6\)
Thấy: \(VT\le VP=6\)\(\Rightarrow VT=VP=6\)
\(\Rightarrow\left(x-4\right)^4+8\left(x-4\right)^3+17\left(x-4\right)^2+6=6\)
Suy ra x=4
ko hiểu chỗ nào ib nhé
Đúng 0
Bình luận (0)
lời giải của bạn trên có 1 xíu sai nhé
Là BĐT Bu-nhi-a Cốp-xki chứ ạ ?
Đúng 0
Bình luận (0)
KN
14 tháng 3 2020 lúc 20:20
Giải phương trình:
\(\sqrt{13x^2-6x+10}+\sqrt{5x^2-13x+\frac{17}{2}}+\sqrt{17x^2-48x+36}=\frac{1}{2}\left(36x-8x^2-21\right)\)
đánh giá thôi bạn
\(VT=\sqrt{\left(3x+1\right)^2+\left(2x-3\right)^2}+\sqrt{\left(2x-\frac{5}{2}\right)^2+\left(x-\frac{3}{2}\right)^2}+\sqrt{x^2+\left(4x-6\right)^2}\)
\(\ge\sqrt{\left(3x+1\right)^2}+\sqrt{\left(2x-\frac{5}{2}\right)^2}+\sqrt{x^2}=\left|3x+1\right|+\left|2x-\frac{5}{2}\right|+\left|x\right|\)
\(\ge\left|3x+1+2x-\frac{5}{2}+x\right|=\left|6x-\frac{3}{2}\right|\ge6x-\frac{3}{2}\)
Dấu "=" xảy ra khi x = \(\frac{3}{2}\)
\(VP=\frac{1}{2}\left[-2\left(2x-3\right)^2+12x-3\right]\le\frac{1}{2}\left(12x-3\right)=6x-\frac{3}{2}\)
Dấu "=" xảy ra khi x = \(\frac{3}{2}\)
Từ đó suy ra nghiệm phương trình là \(x=\frac{3}{2}\)
\(15x^3-3x^5-6x^2-8x^3-2x+11-3x^5-17x^3+6x^2\)
ta có : ( 15x3 -8x3-17x3) - (3x5+3x5)+(6x2 - 6x2)-2x+11 = -10x3 -2x + 11