b1 :tìm x
2x = 4,128
b2 :so sánh các cặp số
a, A = 275 và B= 2433
b,A = 2300 và B = 3300
giúp mk với
so sánh:
a)A=275 và B=2433
b)A=2300 và B=3200
a)
Ta có : A = 275 = (33)5 = 315
B = 2433 = (35)3 = 315
Vì 315 = 315 => A = B
b )
Ta có : A = 2300 = (23)100 = 8100
B = 3200 = (32)100 = 9100
Vì 8100 < 9100 => A<B
So snhs các cặp số sau :
a. A = 275 và B = 2433
b. A = 2300 và B = 3200
Cho hình vẽ sau,biết:A1=B1
a) So sánh các cặp góc đồng vị?
b) So sánh các cặp góc so le trong?
c) Tính A4 +B1;A3 và B2. Nêu nhận xét.
Các cặp góc đồng vị và so le trong và so le ngoài luôn bằng nhau
Còn các cặp góc trong cùng phía và ngoài cùng phía thì bù nhau
Cho đường thẳng c cắt hai đường a,b và lần lượt tại A và B và cho biết A3=B1
So sánh các cặp góc đồng vị và góc so le trong còn lại
Cho a//b,c cắt a và b tại A và B . A và B [ A1 = B1 = 40 Độ là so le trong ] Hảy tính các cặp góc so le trong và đồng vị còn lại
B1: so sánh:a) A=1+2+3+......+1000 và B= 1.2.3..11
b) A= 1.2.3...20 và B=1+2+3+...+1000000
B2: so sánh các số tự nhiên a và b:
1+2+3+...+a/a < 1+2+3+...+b/b
Bài 1: So sánh
1/ a) 2300 và 3200 b) 9920 và 999910 c) 3500 và 7300
d) 202303 và 303202 e) 10750 và 7375
a) \(2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}\)
\(\Rightarrow2^{300}< 3^{200}\)
b) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\Rightarrow99^{20}< 9999^{10}\)
c) \(3^{500}=\left(3^5\right)^{100}=243^{100}\)
\(7^{300}=\left(7^3\right)^{100}=343^{100}>243^{100}\)
\(\Rightarrow3^{500}< 7^{300}\)
\(\left(d\right):202^{303}=\left(202^3\right)^{101}=8242408^{101}>303^{202}=\left(303^2\right)^{101}=91809^{101}\)
\(\left(e\right):107^{50}=\left(107^2\right)^{25}=11449^{25}< 73^{75}=\left(73^3\right)^{25}=389017^{25}\)
so sánh A= -15/2300 + -17/3200
B=-17/2300 + -15/3200
Cho hình vẽ bên, biết a // b và B ^ 2 = 45 0
a). Tính số đo A ^ 1
b). So sánh A ^ 3 và B ^ 1
c). Tính A ^ 2 + B 1 ^
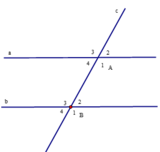
a) Vì B 2 ^ , A 1 ^ là cặp góc trong cùng phía nên ta có:
B 2 ^ + A 1 ^ = 180 0 ⇒ A 1 ^ = 180 0 − B 2 ^ = 180 0 − 45 0 = 135 0 .
b) Ta có B ^ 1 = A ^ 1 = 135 ∘ (hai góc đồng vị)
mà A ^ 3 = A ^ 1 = 135 ∘ (hai góc đối đỉnh)
Vậy B ^ 1 = A ^ 3 = 135 ∘
c) Ta có A ^ 1 + A ^ 2 = 180 ∘ (hai góc kề bù) mà B ^ 1 = A ^ 1 (theo câu b)
Do đó A ^ 2 + B ^ 1 = 180 ∘