a) ĐS: ; b) ĐS: 26; c) ĐS: 12a

d) - = - 6a + 9 -

= - 6a + 9 - = - 6a + 9 - 6│a│.

Khi a ≥ 0 thì │a│= a.

Do đó - = - 6a + 9 -6a = - 12a + 9.

Khi a < 0 thì │a│= a.

Do đó - = - 6a + 9 + 6a = + 9.

a: \(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(=\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{4}+\sqrt{6}+\sqrt{8}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(=1+\sqrt{2}\)

b: \(\sqrt{\dfrac{2a}{3}}\cdot\sqrt{\dfrac{3a}{8}}=\sqrt{\dfrac{6a^2}{24}}=\sqrt{\dfrac{a^2}{4}}=\dfrac{a}{2}\)

c: \(\sqrt{5a\cdot45a}-3a=-15a-3a=-18a\)

\(1) \sqrt{9a^2.b^2}\)=3ab

\(2) \sqrt{3a}.\sqrt{27a}=\sqrt{3a}.3\sqrt{3a}=9a\)

\(3) \sqrt{3a^5}.12a=12\sqrt{3a^7}\)

\(4) \sqrt{5a}.\sqrt{45a}-3a=15a-3a=12a\)

\(5) \sqrt{3+\sqrt{a}}.\sqrt{3-\sqrt{a}}=\sqrt{(3+\sqrt{a}).(3-\sqrt{a})} =\sqrt{9-a} \)

\(6) \sqrt{3+\sqrt{5}}.\sqrt{3\sqrt{5}} =\sqrt{\sqrt{3\sqrt{5}}.(3+\sqrt{5})} =\sqrt{9+\sqrt{15}}\)

1) \(\sqrt{9a^2b^2}=3ab\)

2) \(\sqrt{3a}\cdot\sqrt{27a}=9a\)

4) \(\sqrt{5a}\cdot\sqrt{45a}-3a=15a-3a=12a\)

\(\sqrt{5a}×\sqrt{45a}=\sqrt{15^2a^2}=15a\)

a) Ta có: \(\sqrt{27\cdot48\left(1-a^2\right)}\)

\(=\sqrt{3^4\cdot4^2\cdot\left(1-a^2\right)}\)

\(=36\sqrt{1-a^2}\)

c) Ta có: \(\sqrt{5a}\cdot\sqrt{45a}-3a\)

\(=15a-3a=12a\)

b) Ta có: \(B=\dfrac{1}{a-b}\cdot\sqrt{a^4\cdot\left(a-b\right)^2}\)

\(=\dfrac{1}{a-b}\cdot a^2\cdot\left(a-b\right)\)

\(=a^2\)

d) Ta có: \(D=\left(3-a\right)^2-\sqrt{0.2}\cdot\sqrt{180a^2}\)

\(=a^2-6a+9-\sqrt{36a^2}\)

\(=a^2-6a+9-\left|6a\right|\)

\(=\left[{}\begin{matrix}a^2-6a+9-6a\left(a\ge0\right)\\a^2-6a+9+6a\left(a< 0\right)\end{matrix}\right.\)

\(=\left[{}\begin{matrix}a^2-12a+9\\a^2+9\end{matrix}\right.\)

\(A=9.4\left|1-a\right|=36\left(a-1\right)\) (a>1)

\(B=\dfrac{a^2\left|a-b\right|}{a-b}=\dfrac{a^2\left(a-b\right)}{a-b}=a^2\) (a>b)

\(C=5.3\left|a\right|-3a=15a-3a=12a\)

\(D=9-6a+a^2-6\left|a\right|=\left[{}\begin{matrix}a^2-12a+9\left(a\ge0\right)\\a^2+9\left(a< 0\right)\end{matrix}\right.\) 

a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)

do \(a\ge0\)

b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)

c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)

\(=15a-3a=12a\)do a > 0 

d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)

\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)

Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)

Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)

a) Ta có:

b) Ta có:

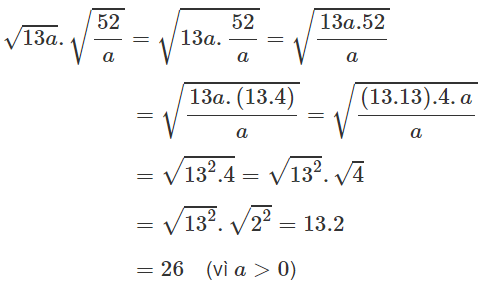
c) Do a ≥ 0 nên bài toán luôn xác định. Ta có:

d) Ta có:

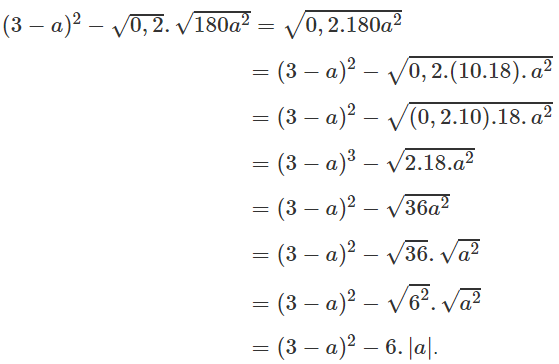
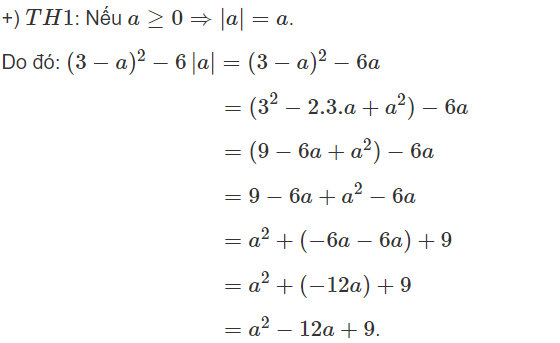
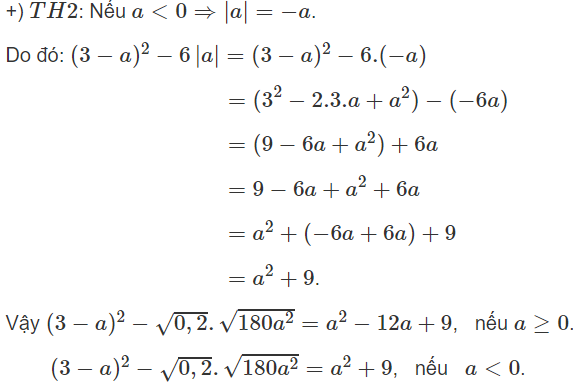
b) \(\sqrt{13a}\).\(\sqrt{\frac{52}{a}}\)=\(\sqrt{13a.\frac{52}{a}}\)=\(\sqrt{13.13.2.2}\)=13.2=26

a)\(\sqrt{4\left(a-3\right)^2}=\sqrt{2^2\left(a-3\right)^2}=\sqrt{\left(2a-6\right)^2}=2a-6\)

b) \(\sqrt{9\left(b-2\right)^2}=\sqrt{3^2\left(b-2\right)^2}=\sqrt{\left[3\left(b-2\right)\right]^2}=3b-6\)

c) bạn xem lại đề

d)
\(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\sqrt{\left(15a\right)^2}-3a=15a-3a=12a\)

e) \(\dfrac{\sqrt{48x^3}}{\sqrt{3x^5}}=\sqrt{\dfrac{48x^3}{3x^5}}=\sqrt{\dfrac{16}{x^2}}=\dfrac{\sqrt{16}}{\sqrt{x^2}}=\dfrac{4}{x}\)