a, \(A=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{x-9}\right):\left(\dfrac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\)

\(=\left[\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{3x+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\right]:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\)

\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\)

\(=\dfrac{-3\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}:\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)

\(=\dfrac{-3}{\sqrt{x}+3}\)

b, \(A\in Z\Leftrightarrow\dfrac{-3}{\sqrt{x}+3}\in Z\)

\(\Leftrightarrow\sqrt{x}+3\inƯ_3=\left\{\pm1;\pm3\right\}\)

\(\Leftrightarrow\sqrt{x}=0\)

\(\Leftrightarrow x=0\)

\(a,A=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{x-9}\right):\left(\dfrac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\left(x\ge0;x\ne9\right)\\ A=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\\ A=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\\ A=\dfrac{-3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{-3}{\sqrt{x}+3}\)

\(b,A\in Z\Leftrightarrow\dfrac{-3}{\sqrt{x}+3}\in Z\Leftrightarrow-3⋮\sqrt{x}+3\\ \Leftrightarrow\sqrt{x}+3\inƯ\left(-3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-4;-2;0\right\}\)

Mà \(\sqrt{x}\ge0\)

\(\Leftrightarrow x\in\left\{0\right\}\)

Vậy \(x=0\) thì A nguyên

a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)

do \(a\ge0\)

b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)

c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)

\(=15a-3a=12a\)do a > 0 

d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)

\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)

Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)

Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)

a) Ta có:

b) Ta có:

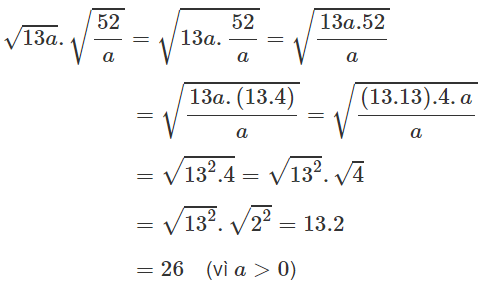
c) Do a ≥ 0 nên bài toán luôn xác định. Ta có:

d) Ta có:

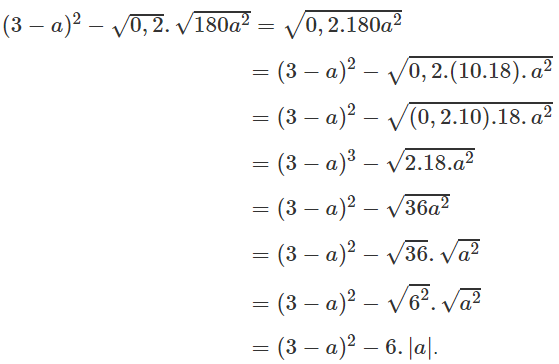
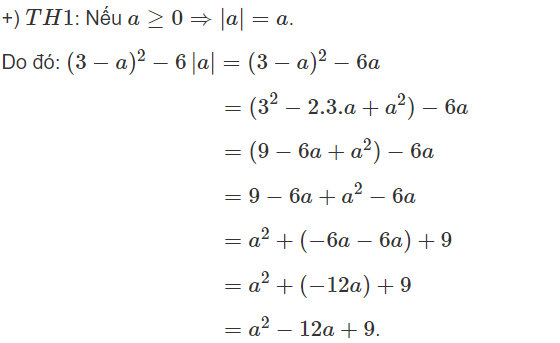
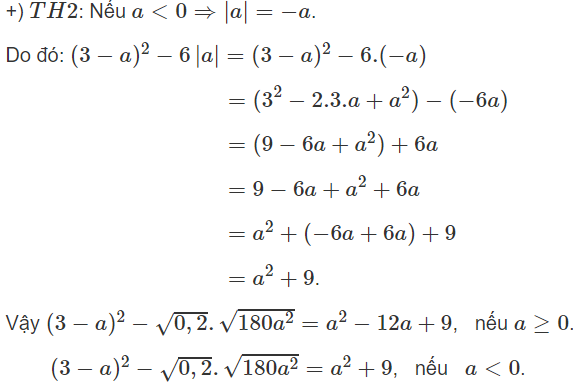
b) \(\sqrt{13a}\).\(\sqrt{\frac{52}{a}}\)=\(\sqrt{13a.\frac{52}{a}}\)=\(\sqrt{13.13.2.2}\)=13.2=26

a, \(2\sqrt{a^2}-5a=2\left|a\right|-5a\)do a < 0 

\(=-2a-5a=-7a\)

b, \(\sqrt{25a^2}+3a=\sqrt{\left(5a\right)^2}+3a=\left|5a\right|+3a\)do \(a\le0\)

TH1 : \(-5a+3a=-2a\)với \(a< 0\)

hoặc TH2 : \(5+3=8\)

c, \(\sqrt{9a^4}+3a^2=\sqrt{\left(3a^2\right)^2}+3a^2=\left|3a^2\right|+3a^2\)

\(=3a^2+3a^2=6a^2\)do \(3>0;a^2\ge0\forall a\Rightarrow3a^2\ge0\forall a\)

d, \(5\sqrt{4a^6}-3a^3=5\sqrt{\left(2a^3\right)^2}-3a^3\)

\(=5\left|2a^3\right|-3a^3=-10a^3-3a^3=-13a^3\)do \(a< 0\Rightarrow a^3< 0\)

a) \(2\sqrt{a^2}-5a\)=2\(|a|\)-5a = -2a-5a=-7a

b) \(\sqrt{25a^2}\) +3a = 5\(|a|\) + 3a=5a+3a=8a.

c) \(\sqrt{9a^4}\) + 3\(a^2\)=6\(a^2\)

d) \(5\sqrt{4a^6}\) - 3\(a^3\)=-13\(a^3\)

a, 2|a| - 5a = -2a - 5a = -7a

b, 5|a|+3a = 5a + 3a = 8a

c, |3a^2| + 3a^2 = 3a^2 + 3a^2 = 6a^2

d, 5|2a^3| - 3a^3 = 5. (-2a^3) - 3a^3 = -10a^3- 3a^3=-13a^3

2) năm mới chúc nhau niềm vui ( cho bài dễ thôi )

Vt >/ 3 + 2 = 5

 VP </ 5 

dấu = xảy ra  khi x =-1

Dùng Hằng Đẳng Thức thôi bạn ạ

Minh Triều bạn làm giúp mk đi, mk ko làm đc

a) \(\sqrt{\dfrac{2a}{3}}\cdot\sqrt{\dfrac{3a}{8}}\)

\(=\sqrt{\dfrac{2a\cdot3a}{3\cdot8}}\)

\(=\sqrt{\dfrac{6a^2}{24}}\)

\(=\sqrt{\dfrac{a^2}{4}}\)

\(=\dfrac{\sqrt{a^2}}{\sqrt{4}}\)

\(=\dfrac{a}{2}\)

b) \(\sqrt{3a}\cdot\sqrt{\dfrac{52}{a}}\)

\(=\sqrt{3a\cdot\dfrac{52}{a}}\) 

\(=\sqrt{3\cdot52}\)

\(=\sqrt{13\cdot3\cdot4}\)

\(=2\sqrt{39}\)

c) \(2y^2\cdot\sqrt{\dfrac{x^4}{4y^2}}\)

\(=2y^2\cdot\dfrac{\sqrt{\left(x^2\right)^2}}{\sqrt{\left(2y\right)^2}}\)

\(=2y^2\cdot\dfrac{x^2}{-2y}\)

\(=\dfrac{2y^2\cdot x^2}{-2y}\)

\(=-x^2y\)

a

\(\sqrt{9\left(2-3x\right)^2}=6\\ \Leftrightarrow3\left|2-3x\right|=6\\ \Leftrightarrow\left|2-3x\right|=2\)

Với \(x\le\dfrac{2}{3}\) thì PT trở thành:

\(2-3x=2\\ \Leftrightarrow3x=0\\ \Leftrightarrow x=0\left(nhận\right)\)

Với \(x>\dfrac{2}{3}\) thì PT trở thành:

\(3x-2=2\\ \Leftrightarrow3x=4\\ \Leftrightarrow x=\dfrac{4}{3}\left(nhận\right)\)

b

ĐK: \(x\ge-\dfrac{3}{2}\)

\(\sqrt{4x^2-9}=2\sqrt{2x+3}\\ \Leftrightarrow\sqrt{\left(2x\right)^2-3^2}=2\sqrt{2x+3}\\ \Leftrightarrow\sqrt{2x-3}.\sqrt{2x+3}-2\sqrt{2x+3}=0\\ \Leftrightarrow\sqrt{2x+3}\left(\sqrt{2x-3}-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{2x+3}=0\\\sqrt{2x-3}-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\2x-3=4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\left(nhận\right)\\x=\dfrac{7}{2}\left(nhận\right)\end{matrix}\right.\)

c

ĐK: \(x\ge3\)

\(\sqrt{10\left(x-3\right)}=\sqrt{20}\\ \Leftrightarrow10\left(x-3\right)=20\\ \Leftrightarrow x-3=2\\ \Leftrightarrow x=5\left(nhận\right)\)

d

\(\sqrt{x^2+6x+9}=3x-6\\ \Leftrightarrow\sqrt{\left(x+3\right)^2}=3x-6\\ \Leftrightarrow\left|x+3\right|=3x-6\)

Với \(x\ge-3\) thì PT trở thành:

\(x+3=3x-6\\ \Leftrightarrow x+3-3x+6=0\\ \Leftrightarrow-2x+9=0\\ \Leftrightarrow x=\dfrac{9}{2}\left(nhận\right)\)

Với \(x< -3\) thì PT trở thành:

\(-x-3=3x-6\\ \Leftrightarrow-x-3-3x+6=0\\ \Leftrightarrow-2x+3=0\\ \Leftrightarrow x=\dfrac{3}{2}\left(loại\right)\)