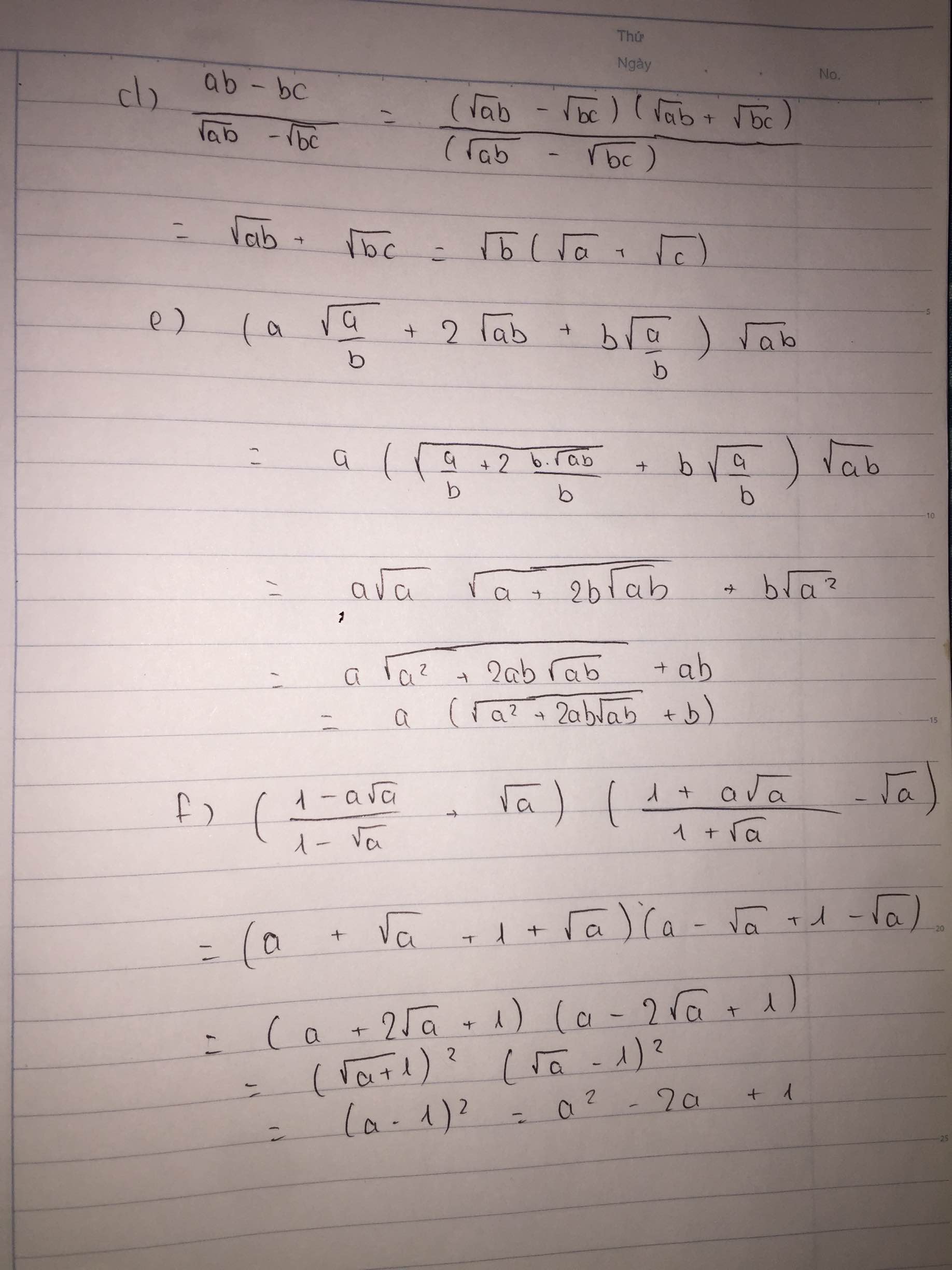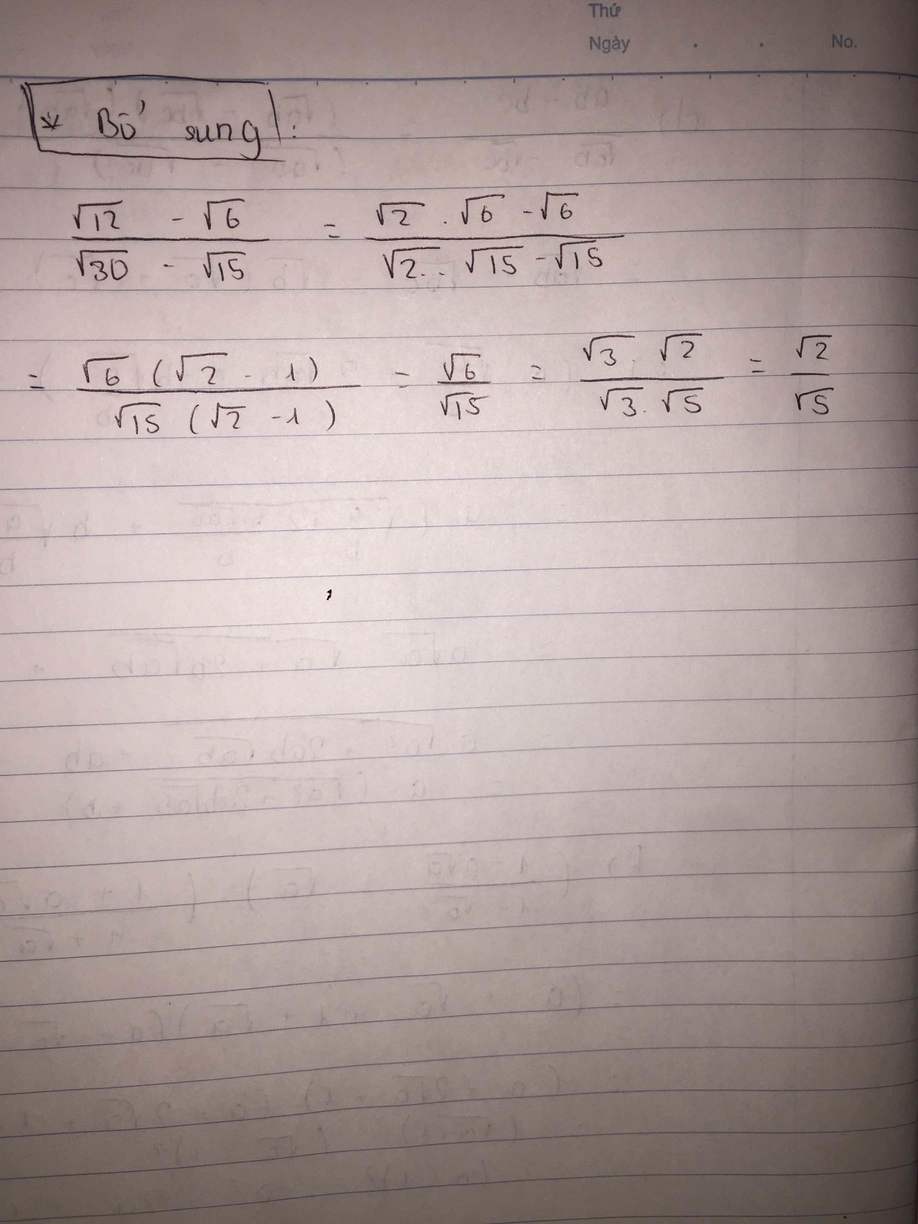Giúp em bai 1 với câu e với f thôi ạ
DA
Những câu hỏi liên quan
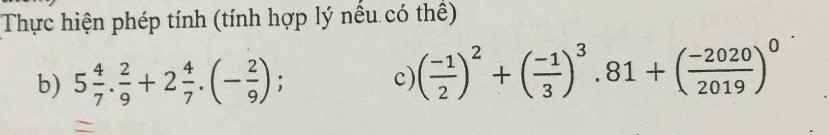
Giúp e với ạ, 1 câu thôi cx đc ạ!
b: \(=\dfrac{39}{7}\cdot\dfrac{2}{9}+\dfrac{18}{7}\cdot\dfrac{-2}{9}=\dfrac{2}{9}\cdot3=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
Moị người giúp em bài 1 câu d,e,f với ạ
mọi ng giải giúp em câu e,f bài 1 với ạ
e:
\(E=\left(\dfrac{\sqrt{15}-\sqrt{20}}{2-\sqrt{3}}+\dfrac{\sqrt{21}-\sqrt{7}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{5}\left(2-\sqrt{3}\right)}{2-\sqrt{3}}-\dfrac{\sqrt{7}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right)\cdot\dfrac{\sqrt{7}-\sqrt{5}}{1}\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
=-2
f: \(F=\sqrt{3}+1+2-\sqrt{3}=3\)
Đúng 2
Bình luận (0)
Cho tam giac abc vuông goc tai a, ve ah vuông goc với bc tai h A, cm tam giac abc đồng C, Vẽ tia phân giác trong của góc ABC cắt Ah tại F cắt ACtaij E. Chứng minh rằng HF.CE=AE.À Câu a em làm được rồi. Chỉ cằn câu c thôi ạ nhanh giúp em với 3
 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)
Đúng 1
Bình luận (0)
giúp em hai câu e,f cuối với ạ 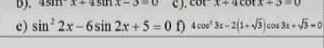
e) \(sin^22x-6sin2x+5=0\Rightarrow\) \(\left[{}\begin{matrix}sin2x=5\left(loại\right)\\sin2x=1\end{matrix}\right.\)
\(\Rightarrow sin2x=sin\left(\dfrac{\pi}{2}\right)\)
\(\Rightarrow2x=\dfrac{\pi}{2}+k2\pi\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
f.
\(4cos^23x-2\left(\sqrt{3}+1\right)cos3x+\sqrt{3}=0\)
\(\Leftrightarrow4cos^23x-2cos3x-2\sqrt{3}cos3x+\sqrt{3}=0\)
\(\Leftrightarrow2cos3x\left(2cos3x-1\right)-\sqrt{3}\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left(2cos3x-\sqrt{3}\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\\cos3x=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Giúp em giải
bài 1 tìm nghiệm các hàm số: p, o, l, q
bài 2 câu e, f với ạ
em cám ơn ạ 

j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.
Đúng 1
Bình luận (0)
giúp mik câu d,e,f thôi ạ
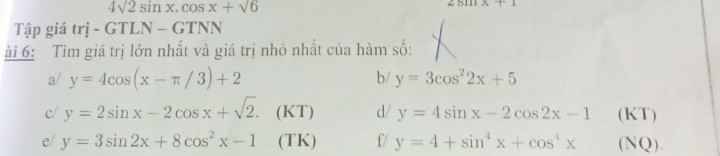
d) \(y=4sinx-2cos2x-1\)
\(=4sinx-2\left(1-2sin^2x\right)-1\)
\(=4sin^2x+4sinx-3\)
Đặt \(t=sinx,t\in\left[-1;1\right]\)
\(y=f\left(t\right)=4t^2+4t-3\) \(\Leftrightarrow f'\left(t\right)=8t+4\)
\(f'\left(t\right)=0\Leftrightarrow t=-\dfrac{1}{2}\)
Vẽ BBT với \(t\in\left[-1;1\right]\) ta được
\(minf\left(t\right)=miny=-4\Leftrightarrow t=-\dfrac{1}{2}\)\(\Leftrightarrow sinx=-\dfrac{1}{2}\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\) ( k thuộc Z)
\(maxf\left(t\right)=miny=5\Leftrightarrow t=1\)\(\Leftrightarrow sinx=1\) \(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\) ( k thuộc Z)
Vậy...
Đúng 2
Bình luận (0)
e) \(y=3sin2x+8cos^2x-1\)
\(=3sin2x+4\left(2cos^2x-1\right)+3\)
\(=3sin2x+4cos2x+3\)
\(=5\left(\dfrac{3}{5}sin2x+\dfrac{4}{5}cos2x\right)+3\)
Đặt \(cosu=\dfrac{3}{5}\Leftrightarrow sinu=\dfrac{4}{5}\)
\(y=5\left(sin2x.cosu+cos2x.sinu\right)+3=5.sin\left(2x+u\right)+3\)
Có \(-1\le sin\left(2x+u\right)\le1\) \(\Leftrightarrow-2\le y\le8\)
\(maxy=8\Leftrightarrow sin\left(2x+u\right)=1\) \(\Leftrightarrow2x+u=\dfrac{\pi}{2}+k2\pi\) \(\Leftrightarrow x=-\dfrac{u}{2}+\dfrac{\pi}{4}+k\pi\)\(\Leftrightarrow x=-\dfrac{1}{2}.arccos\dfrac{3}{5}+\dfrac{\pi}{4}+k\pi\) ( k thuộc Z)
\(miny=-2\Leftrightarrow sin\left(2x+u\right)=-1\)\(\Leftrightarrow x=-\dfrac{1}{2}.\dfrac{arccos3}{5}-\dfrac{\pi}{4}+k\pi\) ( k thuộc Z)
Vậy...
Đúng 2
Bình luận (0)
f)\(y=4+sin^4x+cos^4x\)
\(=4+\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=4+1-\dfrac{1}{2}\left(2sinx.cosx\right)^2\)
\(=5-\dfrac{1}{2}.\left(sin2x\right)^2\)
\(\left(sin2x\right)^2\in\left[0;1\right]\Leftrightarrow y\in\left[\dfrac{9}{2};\dfrac{11}{2}\right]\)
\(maxy=\dfrac{11}{2}\Leftrightarrow sin2x=0\Leftrightarrow2x=k\pi\Leftrightarrow x=\dfrac{k\pi}{2}\) ( k thuộc Z )
\(miny=\dfrac{9}{2}\Leftrightarrow\left(sin2x\right)^2=1\)\(\Leftrightarrow cos2x=0\)\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\) ( k thuộc Z )
Vậy...
Đúng 1
Bình luận (0)
Giải giúp em câu bcdef với ạ riêng b,e,f giải đưa về cos giúp em
b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)
Đúng 1
Bình luận (0)
d.
\(\Leftrightarrow\dfrac{\sqrt{2}}{2}sinx-\dfrac{\sqrt{2}}{2}cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời