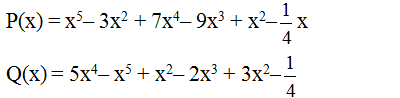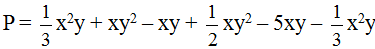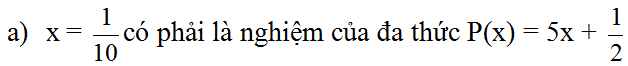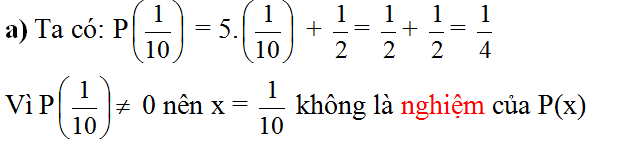Giải bài tập toán sgk nhân đơn thức với đa thức
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NT
Những câu hỏi liên quan
Giải bài tap 4 trong sgk bài nhân đơn thức với đa thuc toán tâp 1
gọi số tuổi là x ta có :[2 . (x+5) +10 ] -100= (2x +10 +10) .5 -100
=(2x +20 ) .5 -100
=10x +100-100
=10x
thực chất kq này chính gấp 10 lần tuổi bạn, khi đọc kq cuối cùng chỉ cần bỏ số 0 cuối cùng thì là ra tuổi cúa bạn vd đọc 130 thì bỏ số 0 thì số cuối cùng là tuổi bạn
Đúng 0
Bình luận (0)
Nhân đa thức với đa thức
Trả lời câu hỏi Toán 8 Tập 1 Bài 2 trang 7: Nhân đa thức 
\(\left(\frac{1}{2}xy-1\right).\left(x^3-2x-6\right)=\frac{1}{2}xy.\left(x^3-2x-6\right)+\left(-1\right).\left(x^3-2x-6\right)\)
= \(\frac{1}{2}xy.x^3+\frac{1}{2}xy.\left(-2x\right)+\frac{1}{2xy}.\left(-6\right)+\left(-1\right).x^3+\left(-1\right).\left(-2x\right)+\left(-1\right).\left(-6\right)\)
= \(\frac{1}{2}x^{\left(1+3\right)}y-x^{\left(1+1\right)}y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^2y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^3-x^2y-3xy+2x+6\)
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
Bài làm
Ta có: ( xy - 1 )( x3 - 2x - 6 )
= ( xy . x3 ) + [ xy . ( -2x ) ] + [ xy . ( - 6 ) ] + [ ( -1 ) . x3 ] + [ ( -1 ) . ( -2x ) ] + [ ( -1 ) . ( -6 ) ] ( * chỗ này nếu thầnh thạo phép nnhân đa thức r thì k cần pk ghi đâu )
= x4y - 2x2y - 6xy - x3 + 2x + 6
# Học tốt #
Đúng 0
Bình luận (0)
Giải các bài tập trong sách giáo khoa bài nhân đơn thức với đa thức
Cùng ôn tập lại HKI Toán 8.Phần I: Đại số.Chương I: Phép nhân và phép chia các đa thức.Câu 1: Nêu quy tắc nhân đơn thức với đa thức, đa thức với đa thức?Câu 2: Có bao nhiêu hằng đẳng thức đáng nhớ? Viết công thức?Câu 3: Có bao nhiêu cách phân tích đa thức thành nhân tử (không nêu cách nâng cao)?Câu 4: Nêu quy tắc chia đơn thức với đơn thức, đa thức với đơn thức?Câu 5: Trong phép chia đa thức một biến đã sắp xếp, Q(x), R(x) được gọi là gì? Bậc của R(x) có mối quan hệ gì với bậc của Q(x)?
Đọc tiếp
Cùng ôn tập lại HKI Toán 8.
Phần I: Đại số.
Chương I: Phép nhân và phép chia các đa thức.
Câu 1: Nêu quy tắc nhân đơn thức với đa thức, đa thức với đa thức?
Câu 2: Có bao nhiêu hằng đẳng thức đáng nhớ? Viết công thức?
Câu 3: Có bao nhiêu cách phân tích đa thức thành nhân tử (không nêu cách nâng cao)?
Câu 4: Nêu quy tắc chia đơn thức với đơn thức, đa thức với đơn thức?
Câu 5: Trong phép chia đa thức một biến đã sắp xếp, Q(x), R(x) được gọi là gì? Bậc của R(x) có mối quan hệ gì với bậc của Q(x)?
Câu 1:
Nhân từng hạng tử của đa thức/đơn thức này cho từng hạng tử của đa thức/đơn thức kia. Sau đó, thu gọn lại ta được kết quả cần tìm
Câu 2:
Có 7 hằng đẳng thức. Công thức:
1: \(\left(a+b\right)^2=a^2+2ab+b^2\)
2: \(\left(a-b\right)^2=a^2-2ab+b^2\)
3: \(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
4: \(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
5: \(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
6: \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)
7: \(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)
Đúng 4
Bình luận (0)
Cho hai đa thức:
a) Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến.
b) Tính P(x) + Q(x) và P(x) – Q(x).
c) Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không phải là nghiệm của đa thức Q(x).
a) Ta có: M(x) = 5x3 + 2x4 – x2 + 3x2 – x3 – x4 + 1 – 4x3 = x4 + 2x2 + 1 b) Ta có (M1) = 14 + 2.12 + 1 = 1 + 2 + 1 = 4 và (M-1) = (-1)4 + 2.(-1)2 + 1 + 1 + 2 + 1 = 4 c) Ta có M(x) = x4 + 2x2 + 1 = (x2+1)2 Nhận xét: Vì x2 ≥ 0 => x2 + 1 > 1 => (x2 + 1)2 > 1 > 0 với mọi x ∈ R Vậy M(x) = (x2 +1)2 > 0 với mọi x ∈ R. Điều này chứng tỏ rằng M(x) không có nghiệm trong R.
Bạn ơi phần nào có số đằng sau x là mũ nhé! ko biết ấn dấu mũ
Đúng 0
Bình luận (0)
Bài thế mà cũng hỏi! Bạn phải suy nghĩ trước đã chứ!!!
Đúng 0
Bình luận (2)
Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1:
JUP
Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1:
Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1:
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Kiểm tra xem:
b) Mỗi số x = 1; x = 3 có phải là một nghiệm của đa thức Q(x) = x2 – 4x + 3 không.
b) Ta có: Q(1) = 12 – 4.1 + 3 = 1 – 4 + 3 = 0
=> x = 1 là nghiệm của Q(x)
Q(3) = 32 – 4.3 + 3 = 9 – 12 + 3 = 0
=> x = 3 là nghiệm của Q(x)
Đúng 0
Bình luận (0)
Bài 49 (trang 46 SGK Toán 7 tập 2): Hãy tìm bậc của mỗi đa thức sau:
M = x2 – 2xy + 5x2 – 1
N = x2y2 – y2 + 5x2 – 3x2y + 5
nếu có trong sách thì lên google
Đúng 0
Bình luận (0)
\(M=6x^2-2xy-1\left(bậc:2\right)\)
N có bậc 4
Đúng 1
Bình luận (0)
Lời giải:
a) Rút gọn đa thức M ta có :
M = x2 – 2xy + 5x2 – 1 = (x2+ 5x2) – 2xy – 1 = 6x2 – 2xy – 1
Sau khi rút gọn, M có các hạng tử là:
6x2 có bậc 2
– 2xy có bậc 2
– 1 có bậc 0
Bậc của đa thức là bậc của hạng tử có bậc cao nhất
⇒ Đa thức M = x2 – 2xy + 5x2 – 1 có bậc 2.
b) N = x2y2 – y2 + 5x2 – 3x2y + 5 có các hạng tử là
x2y2 có bậc 4 (vì biến x có bậc 2, biến y có bậc 2, tổng là 2 + 2 = 4)
– y2 có bậc 2
5x2 có bậc 2
– 3x2y có bậc 3 (vì biến x có bậc 2, biến y có bậc 1, tổng là 2 + 1 = 3)
5 có bậc 0
Bậc của đa thức là bậc của hạng tử có bậc cao nhất.
⇒ Đa thức N = x2y2 – y2 + 5x2 – 3x2y + 5 có bậc 4
Đúng 1
Bình luận (1)