Bài1 ; Chứng minh rằng
a) ( 10^33 + 8) chia hết cho 2 và 9
b) ( 10^100 + 14) chia hết cho 2 và 3
c) (21^299 + 9) chia hết cho 5
d) 4 x 10^n + 23 chia hết cho 9 với mọi n thuộc N
bài1 :tính nhanh
1997.2003
\(1997.2003=\left(2000-3\right)\left(2000+3\right)=2000^2-3^2=4000000-9=3999991\)
\(1997\cdot2003=\left(2000-3\right)\left(2000+3\right)=3999991\)
Bài1 thôi nhé🙏🙏🙏
Bài 1:
1. ĐKXĐ: \(x\ge0\)
\(x-7\sqrt{x}+10=0\)
\(\Leftrightarrow x-2\sqrt{x}-5\sqrt{x}+10=0\)
\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-2\right)-5\left(\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{x}-5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=5\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=25\end{matrix}\right.\) ( thỏa mãn đk )
Vậy \(S=\left\{4;25\right\}\)
2. ĐKXĐ: \(x\ge4\)
\(\sqrt{x^2-16}-5\sqrt{x-4}=0\)
\(\Leftrightarrow\sqrt{x^2-16}=5\sqrt{x-4}\)
\(\Leftrightarrow x^2-16=25\left(x-4\right)\)
\(\Leftrightarrow x+4=25\)
\(\Leftrightarrow x=21\) ( thỏa mãn đk )
Vậy \(S=\left\{21\right\}\)
3. ĐKXĐ: \(x\ge-4\)
\(\sqrt{x^2-16}-3\sqrt{x+4}=0\)
\(\Leftrightarrow\sqrt{x^2-16}=3\sqrt{x+4}\)
\(\Leftrightarrow x^2-16=9\left(x+4\right)\)
\(\Leftrightarrow x-4=9\)
\(\Leftrightarrow x=13\) ( thỏa mãn đk )
Vậy \(S=\left\{13\right\}\)
Bài 1:
a) ĐKXĐ: \(x\ge0\)
\(x-7\sqrt{x}+10=0\)
\(\Rightarrow x+10=7\sqrt{x}\)
\(\Rightarrow x^2+20x+100=49x\)
\(\Rightarrow x^2-29x+100=0\)
\(\Rightarrow\left(x^2-4x\right)-\left(25x-100\right)=0\)
\(\Rightarrow\left(x-4\right)\left(x-25\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-4=0\\x-25=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=4\\x=25\end{matrix}\right.\)
b) ĐKXĐ:\(\left\{{}\begin{matrix}x^2-16\ge0\\x-4\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\left(x-4\right)\left(x+4\right)\ge0\\x-4\ge0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x+4\ge0\\x-4\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge-4\\x\ge4\end{matrix}\right.\Rightarrow x\ge4\)
\(\sqrt{x^2-16}-5\sqrt{x-4}=0\)
\(\Rightarrow\sqrt{\left(x-4\right)\left(x+4\right)}-5\sqrt{x-4}=0\\ \Rightarrow\sqrt{x-4}\left(\sqrt{x+4}-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x-4}=0\\\sqrt{x+4}-5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x-4=0\\\sqrt{x+4}=5\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=4\\x+4=25\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=4\\x=21\end{matrix}\right.\)
4. ĐKXĐ: \(x\ge-7\)
\(\sqrt{x^2-49}-3\sqrt{x+7}=0\)
\(\Leftrightarrow\sqrt{x^2-49}=3\sqrt{x+7}\)
\(\Leftrightarrow x^2-49=9\left(x+7\right)\)
\(\Leftrightarrow x-7=9\)
\(\Leftrightarrow x=16\) ( thỏa mãn đk )
Vậy \(S=\left\{16\right\}\)
5. ĐKXĐ: \(x\ge0\)
\(x-14\sqrt{x}+45=0\)
\(\Leftrightarrow\left(\sqrt{x}-9\right)\left(\sqrt{x}-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-9=0\\\sqrt{x}-5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=9\\\sqrt{x}=5\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=81\\x=25\end{matrix}\right.\)
Vậy \(S=\left\{81;25\right\}\)
6. ĐKXĐ: \(x\ge0\)
\(x-13\sqrt{x}+42=0\)
\(\Leftrightarrow\left(\sqrt{x}+6\right)\left(\sqrt{x}+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}+7=0\\\sqrt{x}+6=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=-7\\\sqrt{x}=-6\end{matrix}\right.\) ( loại )
Vậy phương trình vô nghiệm
mng làm giùm em bài1 nha 
Dịch bài1 2 ra tiếng viêy dùm ạ
Bài1: Tìm tập xác định của hàm số


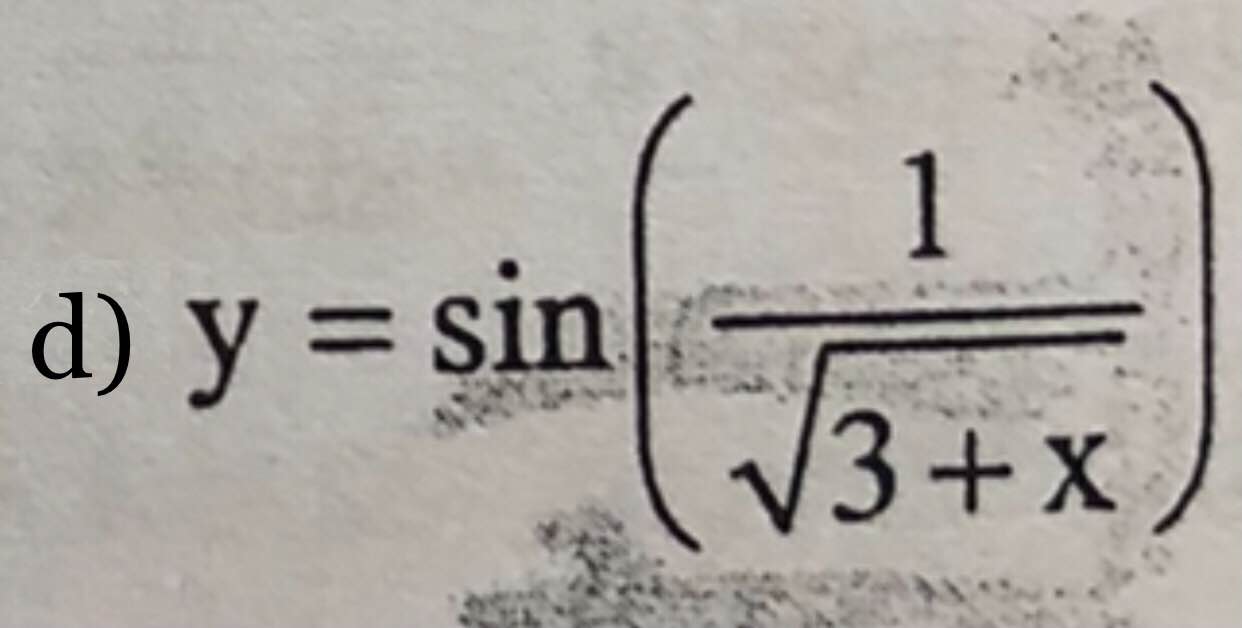
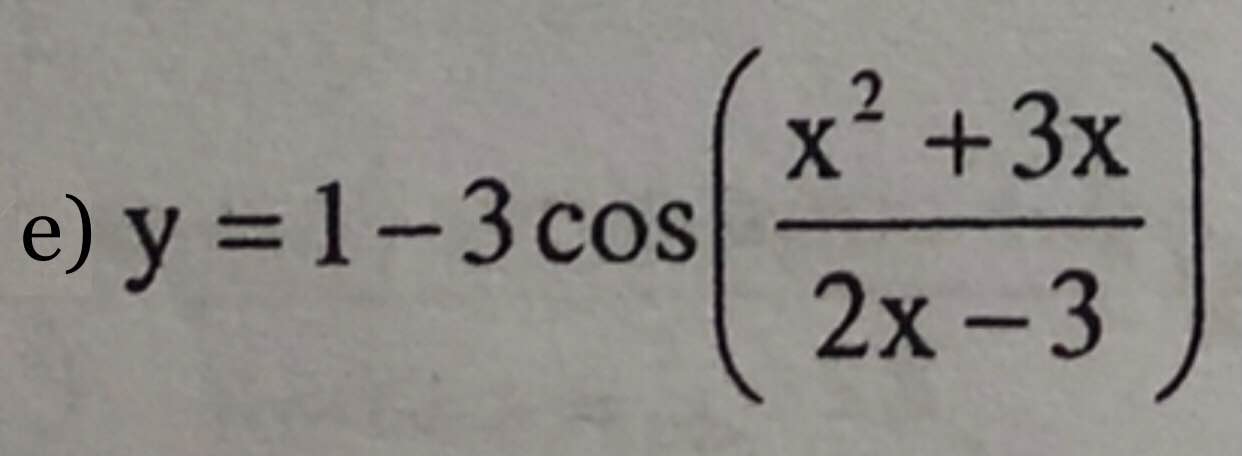
ĐKXĐ:
a.
\(1-sinx\ne0\)
\(\Leftrightarrow sinx\ne1\)
\(\Leftrightarrow x\ne\dfrac{\pi}{2}+k2\pi\)
b.
\(sin\left(2-x\right)\ne0\)
\(\Leftrightarrow2-x\ne k\pi\)
\(\Leftrightarrow x\ne2+k\pi\)
c.
\(1-cos5x\ne0\)
\(\Leftrightarrow cos5x\ne1\)
\(\Leftrightarrow5x\ne k2\pi\)
\(\Leftrightarrow x\ne\dfrac{k2\pi}{5}\)
d.
\(3+x>0\)
\(\Leftrightarrow x>-3\)
e.
\(2x-3\ne0\)
\(\Leftrightarrow x\ne\dfrac{3}{2}\)

Bài1 tính bằng cách thuận tiện nhất ạ
a) \(198+789+502+311\)
\(=\left(198+502\right)+\left(789+311\right)\)
\(=700+1100\)
\(=1800\)
b) \(15.6.4.125.8\)
\(=\left(15.4\right).6.\left(125.8\right)\)
\(=60.6.1000\)
\(=360000\)
c) \(367+129+133+371+17\)
\(=\left(367+133\right)+\left(129+371\right)+17\)
\(=500+500+17\)
\(=1000+17\)
\(=1017\)
d) \(37.64+37.35+37\)
\(=37.\left(64+35+1\right)\)
\(=37.100\)
\(=3700\)
e) \(3.25.8+4.37.6+2.38.12\)
\(=\left(3.8\right).25+\left(4.6\right).37+\left(2.12\right).38\)
\(=24.25+24.37+24.38\)
\(=24.\left(25+37+38\right)\)
\(=24.100\)
\(=2400\)
f) \(136.48+16.272+68.20.2\)
\(=136.48+16.2.136+68.2.20\)
\(=136.48+32.136+136.20\)
\(=136.\left(48+32+20\right)\)
\(=136.100\)
\(=13600\)
g) \(1+6+11+16+...+46+51\)
Số số hạng là :
\(\left(51-1\right):5+1=11\) ( số )
Tổng là :
\(\left(1+51\right)\times11:2=286\)
Chúc bạn học tốt
Bài1 :câu 3 : x+2 > x-6
\(x+2>x-6\)
\(x-x>-2-6\)
\(0>-8\left(llđ\right)\)
Vậy \(\forall x\in R\) thì \(x+2>x-6\)
bài1 tính 254/22
Ưcln(2,7,56,6,60,1,2)
olp7 vong1 bài1
Bài1. Tìm x
4x +12=-20
\(4x+12=-20\)
\(\Rightarrow4x=-20-12\)
\(\Rightarrow4x=-32\)
\(\Rightarrow x=-32\div4\)
\(\Rightarrow x=-8\)
\(4x+12=-20\)
\(\Rightarrow4x=(-20)-12\)
\(\Rightarrow4\text{x}=-32\)
\(\Rightarrow\text{x}=-\frac{32}{4}\Rightarrow\text{x}=-8\)
Chúc bạn học tốt :>
ĐÁP ÁN CỦA MÌNH LÀ
=> 4x +12 =-20
=> 4x = -20 -12
=> 4x = -32
=>x= -32 :4
=>x = -8
vậy x = -8
tích nhanh cho mình nhé
chúc bạn học tốt nha
OK,BYE