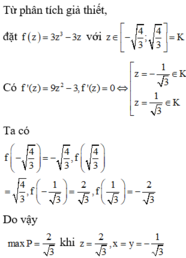Tìm x,y,z thuộc N* thỏa mãn hệ: x+y-z=0 và x3+y3-z2=0.
LQ
Những câu hỏi liên quan
Cho ba số thực x, y, z thay đổi thỏa mãn
x
+
y
+
z
0
x
2
+
y
2
+...
Đọc tiếp
Cho ba số thực x, y, z thay đổi thỏa mãn x + y + z = 0 x 2 + y 2 + z 2 = 2 Tìm giá tri lớn nhất của biểu thức P = x 3 + y 3 + z 3
A. 3 4
B. 2 3
C. 1
D. - 3 2
a) Tìm x,y thỏa mãn x3+y3 +1=3xy tính P= (1+1/x)(1+1/y)(x+y)
b) Cho a+2b+c=0 Tính P= a2/2ab + 4b2/ac + c2/2ab
c) Cho x,y Thỏa mãn x3+y3+8=6xy Tính P=(1 + z/y)(1 + z/x)(x+y)
giúp mik với ạ cảm ơn nhiều nhiều!!!
c) C x(y2 +z2)+y(z2 +x2)+z(x2 +y2)+2xyz.
d) D x3(y−z)+y3(z−x)+z3(x−y).
e) E (x+y)(x2 −y2)+(y+z)(y2 −z2)+(z+x)(z2 −x2).
b) x2 +2x−24 0.
d) 3x(x+4)−x2 −4x 0.
f) (x−1)(x−3)(x+5)(x+7)−297 0.
(2x−1)2 −(x+3)2 0.
c) x3 −x2 +x+3 0.
e) (x2 +x+1)(x2 +x)−2 0.
a) A x2(y−2z)+y2(z−x)+2z2(x−y)+xyz.
b) B x(y3 +z3)+y(z3 +x3)+z(x3 +y3)+xyz(x+y+z). c) C x(y2 −z2)−y(z2 −x2)+z(x2 −y2).
Đọc tiếp
c) C = x(y2 +z2)+y(z2 +x2)+z(x2 +y2)+2xyz.
d) D = x3(y−z)+y3(z−x)+z3(x−y).
e) E = (x+y)(x2 −y2)+(y+z)(y2 −z2)+(z+x)(z2 −x2).
b) x2 +2x−24 = 0.
d) 3x(x+4)−x2 −4x = 0.
f) (x−1)(x−3)(x+5)(x+7)−297 = 0.
(2x−1)2 −(x+3)2 = 0.
c) x3 −x2 +x+3 = 0.
e) (x2 +x+1)(x2 +x)−2 = 0.
a) A = x2(y−2z)+y2(z−x)+2z2(x−y)+xyz.
b) B = x(y3 +z3)+y(z3 +x3)+z(x3 +y3)+xyz(x+y+z). c) C = x(y2 −z2)−y(z2 −x2)+z(x2 −y2).
Đề bài yêu cầu gì vậy em.
Đúng 0
Bình luận (0)
Cho các số thực x, y , z thỏa mãn 2 điều kiện :
a) (x + y) ( y + z)( z + x) = xyz
b) (x3 + y3 ) (y3 + z3) ( x3 + z3) = x3y3z3
CMR: xyz =0
cho 3 số x,y,z thỏa mãn : x+y+z=1; x2+y2+z2=1; x3+y3+z3=1.
tính giá trị biểu thức P= x2008+y2009+x2010
Sửa đề: \(P=x^{2008}+y^{2009}+z^{2010}\)
Ta có: x+y+z=1
nên \(\left(x+y+z\right)^3=1\)
\(\Leftrightarrow x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(x+z\right)=1\)
\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(z+x\right)+1=1\)
\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)
mà 3>0
nên \(\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y=0\\y+z=0\\x+z=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-y\\y=-z\\x=-z\end{matrix}\right.\)
Thay x=-y vào biểu thức \(x+y+z=1\), ta được:
\(-y+y+z=1\)
hay z=1
Thay x=-y và z=1 vào biểu thức \(x^2+y^2+z^2=1\), ta được:
\(\left(-y\right)^2+y^2+1=1\)
\(\Leftrightarrow y^2+y^2=0\)
\(\Leftrightarrow2y^2=0\)
hay y=0
Vì x=-y
và y=0
nên x=0
Thay x=0; y=0 và z=1 vào biểu thức \(P=x^{2008}+y^{2009}+z^{2010}\), ta được:
\(P=0^{2008}+0^{2009}+1^{2010}=1\)
Vậy: P=1
Đúng 4
Bình luận (1)
Tìm x, y thuộc Z thỏa mãn : x3+2x2+3x+2=y3.
Tìm x, y thuộc Z thỏa mãn : x3+2x2+3x+2=y3.
Cho các số x, y, z thỏa mãn đồng thời:x+y+z=1, x2+y2+z2=1,x3+y3+z3=1 Tính giá trị của biểu thức M=x8+y11+z2018
cho x, y, z ≥ 0 thỏa mãn x + y + z =6. Tìm GTNN và GTLN của
A = x2 + y2 + z2
Bạn tham khảo lời giải tại đây:
cho \(x,y,z\ge0\) thỏa mãn \(x y z=6\). tìm GTLN và GTNN của biểu thức \(A=x^2 y^2 z^2\) - Hoc24
Đúng 0
Bình luận (0)