\(B=\left(1+\tan^2\right)\left(1-\sin^2\right)-\left(1+cotan^2\right)\left(1-\cos^2\right)\)
H24
Những câu hỏi liên quan
Tính giá trị biểu thức(e cần gấp ạ)
\(C=\left(1+tan^2a\right)\left(1-sin^2a\right)+\left(1+cotan^2a\right)\left(1-cos^2a\right)\)
Tính:
(sin 1 độ + sin 2 độ + ... + sin 89 độ) - (cos 1 độ + cos 2 độ + ... + cos 89 độ)
Rút gọn:
a) \(\left(\frac{1-\tan^2x}{\tan x}\right)^2-\left(1+\tan^2x\right)\left(1+\cot^2x\right)\)
b) \(\left(\sin^4+\cos^4x-1\right)\left(\tan^2x+\cot^2x+2\right)\)
(sin 1 độ + sin 2 độ + ... + sin 89 độ) - (cos 1 độ + cos 2 độ + ... + cos 89 độ)
=(cos 89 độ +... + cos 2 độ +cos 1 độ) - (cos 1 độ + cos 2 độ + ... + cos 89 độ)
=0
Đúng 0
Bình luận (0)
Giải các PT sau:1. dfrac{left(2cos2x-1right)left(sin x-3right)}{sin x}0 2.dfrac{3left(sin x+cos xright)}{sin x-cos x}2+2cos x3.dfrac{3left(sin x+tan xright)}{tan x-sin x}-2cos x24. 1+sin x+cos x+sin2x+cos2x05. 2sin xleft(1+cos2xright)+sin2x1+2cos x
Đọc tiếp
Giải các PT sau:
1. \(\dfrac{\left(2\cos2x-1\right)\left(\sin x-3\right)}{\sin x}=0\)
2.\(\dfrac{3\left(\sin x+\cos x\right)}{\sin x-\cos x}=2+2\cos x\)
3.\(\dfrac{3\left(\sin x+\tan x\right)}{\tan x-\sin x}-2\cos x=2\)
4. \(1+\sin x+\cos x+\sin2x+\cos2x=0\)
5. \(2\sin x\left(1+\cos2x\right)+\sin2x=1+2\cos x\)
1.
ĐKXĐ: \(x\ne k\pi\)
\(\Leftrightarrow\left(2cos2x-1\right)\left(sinx-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{1}{2}\\sinx=3>1\left(ktm\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
2. Bạn kiểm tra lại đề, pt này về cơ bản ko giải được.
3.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{3\left(sinx+\dfrac{sinx}{cosx}\right)}{\dfrac{sinx}{cosx}-sinx}-2cosx=2\)
\(\Leftrightarrow\dfrac{3\left(1+cosx\right)}{1-cosx}+2\left(1+cosx\right)=0\)
\(\Leftrightarrow\left(1+cosx\right)\left(\dfrac{3}{1-cosx}+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\left(loại\right)\\cosx=\dfrac{5}{2}\left(loại\right)\end{matrix}\right.\)
Vậy pt đã cho vô nghiệm
Đúng 1
Bình luận (1)
4.
\(\Leftrightarrow\left(sin^2x+cos^2x+2sinx.cosx\right)+\left(sinx+cosx\right)+\left(cos^2x-sin^2x\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)^2+\left(sinx+cosx\right)+\left(sinx+cosx\right)\left(cosx-sinx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sinx+cosx+1+cosx-sinx\right)=0\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=0\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{2\pi}{3}+k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Rút gọn biểu thức:
\(B=\left(1+tan^2\alpha\right)\left(1-sin^2\alpha\right)-\left(1+cot^2\alpha\right)\left(1-cos^2\alpha\right)\)
\(B=\left(1+\dfrac{sin^2a}{cos^2a}\right).cos^2a-\left(1+\dfrac{cos^2a}{sin^2a}\right).sin^2a\)
\(=\dfrac{\left(sin^2a+cos^2a\right)}{cos^2a}.cos^2a-\left(\dfrac{sin^2a+cos^2a}{sin^2a}\right).sin^2a\)
\(=1-1=0\)
Đúng 2
Bình luận (0)
a/sin3x+cos2x1+2sin xcos2xb/sin^3x+cos^3x2left(sin^5x+cos^5xright)c/dfrac{tan x}{sin x}-dfrac{sin x}{cos x}dfrac{sqrt{2}}{2}d/dfrac{cos xleft(cos x+2sin xright)+3sin xleft(sin x+sqrt{2}right)}{sin2x-1}1e/sin^2x+sin^23x-2cos^22x0f/dfrac{tan x-sin x}{sin^3x}dfrac{1}{cos x}g/sin2xleft(cos x+tan2xright)4cos^2xh/sin^2x+sin^23xcos^2x+cos^23xk/4sin2xdfrac{cos^2x-sin^2x}{cos^6x+sin^6x}mọi người giải giúp em với em đang cần gấp ạ
Đọc tiếp
a/\(\sin3x+\cos2x=1+2\sin x\cos2x\)
b/\(\sin^3x+\cos^3x=2\left(\sin^5x+\cos^5x\right)\)
c/\(\dfrac{\tan x}{\sin x}-\dfrac{\sin x}{\cos x}=\dfrac{\sqrt{2}}{2}\)
d/\(\dfrac{\cos x\left(\cos x+2\sin x\right)+3\sin x\left(\sin x+\sqrt{2}\right)}{\sin2x-1}=1\)
e/\(\sin^2x+\sin^23x-2\cos^22x=0\)
f/\(\dfrac{\tan x-\sin x}{\sin^3x}=\dfrac{1}{\cos x}\)
g/\(\sin2x\left(\cos x+\tan2x\right)=4\cos^2x\)
h/\(\sin^2x+\sin^23x=\cos^2x+\cos^23x\)
k/\(4\sin2x=\dfrac{\cos^2x-\sin^2x}{\cos^6x+\sin^6x}\)
mọi người giải giúp em với em đang cần gấp ạ
Tìm số đo góc nhọn x:
a) \(4\sin x-1=1\)
b) \(2\sqrt{3}-3\tan x=\sqrt{3}\)
c) \(7\sin-3\cos\left(90^o-x\right)=2,5\)
d) \(\left(2\sin-\sqrt{2}\right)\left(4\cos-5\right)=0\)
e) \(\dfrac{1}{\cos^2x}-\tan x=1\)
f) \(\cos^2x-3\sin^2x=0,19\)
a) \(4sinx-1=1\Leftrightarrow4sinx=2\Leftrightarrow sinx=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow x=30^o\)
b) \(2\sqrt{3}-3tanx=\sqrt{3}\Leftrightarrow3tanx=2\sqrt{3}-\sqrt{3}=\sqrt{3}\Leftrightarrow tanx=\dfrac{\sqrt{3}}{3}\)
\(\Leftrightarrow x=30^o\)
c) \(7sinx-3cos\left(90^o-x\right)=2,5\Leftrightarrow7sinx-3sinx=2,5\Leftrightarrow4sinx=2,5\Leftrightarrow sinx=\dfrac{5}{8}\Leftrightarrow x=30^o41'\)
d)\(\left(2sin-\sqrt{2}\right)\left(4cos-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2sin-\sqrt{2}=0\\4cos-5=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}2sin=\sqrt{2}\\4cos=5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}sin=\dfrac{\sqrt{2}}{2}\\cos=\dfrac{5}{4}\left(loai\right)\end{matrix}\right.\)\(\Rightarrow x=45^o\)
Đúng 2
Bình luận (0)
Xin lỗi nãy đang làm thì bấm gửi, quên còn câu e, f nữa:"(
e) \(\dfrac{1}{cos^2x}-tanx=1\Leftrightarrow1+tan^2x-tanx-1=0\Leftrightarrow tan^2x-tanx=0\Leftrightarrow tanx\left(tanx-1\right)=0\Rightarrow tanx-1=0\Leftrightarrow tanx=1\Leftrightarrow x=45^o\)
f) \(cos^2x-3sin^2x=0,19\Leftrightarrow1-sin^2x-3sin^2x=0,19\Leftrightarrow1-4sin^2x=0,19\Leftrightarrow4sin^2x=0,81\Leftrightarrow sin^2x=\dfrac{81}{400}\Leftrightarrow sinx=\dfrac{9}{20}\Leftrightarrow x=26^o44'\)
Đúng 2
Bình luận (0)
Giải phương trình sau:
a, \(\sin\left(2x\right)+\sin\left(x\right)-\dfrac{1}{2\sin\left(x\right)}-\dfrac{1}{\sin\left(2x\right)}=2\cot\left(2x\right)\)
b, \(\left(\sin\left(2x\right)+cos\left(2x\right)\right)cos\left(x\right)+2cos\left(2x\right)-sin\left(x\right)=0\)
c, \(\sin\left(2x\right)-\cos\left(2x\right)+3\sin\left(x\right)-\cos\left(x\right)-1=0\)
b)
(sin2x + cos2x)cosx + 2cos2x - sinx = 0
⇔ cos2x (cosx + 2) + sinx (2cos2 x – 1) = 0
⇔ cos2x (cosx + 2) + sinx.cos2x = 0
⇔ cos2x (cosx + sinx + 2) = 0
⇔ cos2x = 0
⇔ 2x = 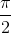 + kπ ⇔ x =
+ kπ ⇔ x = 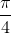 + k
+ k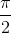 (k ∈
(k ∈ 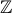 )
)
Đúng 0
Bình luận (0)
c)
Đáp án:
x=π6π6+ k2ππ
và x= 5π65π6+k2ππ (k∈Z)
Lời giải:
sin2x-cos2x+3sinx-cosx-1=0
⇔ 2sinxcosx-(1-2sin²x) +3sinx-cosx-1=0
⇔ 2sin²x+2sinxcosx+3sinx-cosx-2=0
⇔ (2sin²x+3sinx-2)+ cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+2)+cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+cosx+2)=0
⇔ sinx=1212
⇔ x=π6π6+ k2ππ
hoặc x= 5π65π6+k2ππ (k∈Z)
(sinx+cosx+2)=0 (vô nghiệm do sinx+cosx+2=√22sin(x+π4π4)+2>0)
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức
1) tan2a - tan2b = \(\frac{sin\left(a+b\right)\cdot sin\left(a-b\right)}{cos^2a\cdot cos^2b}\)
2) \(\frac{tan\left(a-b\right)+tanb}{tan\left(a+b\right)-tanb}=\frac{cos\left(a+b\right)}{cos\left(a-b\right)}\)
chứng minh đẳng thức lượng giáca) dfrac{1-cos^2left(dfrac{pi}{2}-xright)}{1-sin^2left(dfrac{pi}{2}-xright)} - cotleft(dfrac{pi}{2}-xright) . tanleft(dfrac{pi}{2}-xright) dfrac{1}{sin^2x}b) left(dfrac{1}{cos2x}+1right).tanx tan2x
Đọc tiếp
chứng minh đẳng thức lượng giác
a) \(\dfrac{1-cos^2\left(\dfrac{\pi}{2}-x\right)}{1-sin^2\left(\dfrac{\pi}{2}-x\right)}\) - cot\(\left(\dfrac{\pi}{2}-x\right)\) . tan\(\left(\dfrac{\pi}{2}-x\right)\) = \(\dfrac{1}{sin^2x}\)
b) \(\left(\dfrac{1}{cos2x}+1\right)\).tan\(x\) = \(tan2x\)
Để chứng minh các định lượng đẳng cấp, ta sẽ sử dụng các công thức định lượng giác cơ bản và các quy tắc biến đổi đẳng thức. a) Bắt đầu với phương trình ban đầu: 1 - cos^2(π/2 - x) / (1 - sin^2(π/2 - x)) = -cot(π/2 - x) * tan( π/2 - x) Ta biết rằng: cos^2(π/2 - x) = sin^2(x) (công thức lượng giác) sin^2(π/2 - x) = cos^2(x) (công thức lượng giác) Thay vào phương trình ban đầu, ta có: 1 - sin^2(x) / (1 - cos^2(x)) = -cot(π/2 - x) * tan(π/ 2 - x) Tiếp theo, ta sẽ tính toán một số lượng giác: cot(π/2 - x) = cos(π/2 - x) / sin(π/2 - x) = sin(x) / cos(x) = tan(x) (công thức lượng giác) tan(π/2 - x) = sin(π/2 - x) / cos(π/2 - x) = cos(x) / sin(x) = 1 / tan(x) (công thức lượng giác) Thay vào phương trình, ta có: 1 - sin^2(x) / (1 - cos^2(x)) = -tan(x) * (1/tan(x)) = -1 Vì vậy, ta đã chứng minh là đúng. b) Bắt đầu với phương thức ban đầu: (1/cos^2(x) + 1) * tan(x) = tan^2(x) Tiếp tục chuyển đổi phép tính: 1/cos^2(x) + 1 = tan^2(x) / tan(x) = tan(x) Tiếp theo, ta sẽ tính toán một số giá trị lượng giác: 1/cos^2(x) = sec^2(x) (công thức) lượng giác) sec^2(x) + 1 = tan^2(x) + 1 = sin^2(x)/cos^2(x) + 1 = (sin^2(x) + cos^2(x) ))/cos^2(x) = 1/cos^2(x) Thay thế vào phương trình ban đầu, ta có: 1/cos^2(x) + 1 = 1/cos^2(x) Do đó, ta đã chứng minh được b)đúng.
Đúng 0
Bình luận (0)



