y = x-1+1/x
tính y' , xác định khoảng đồng biến và nghịch biến
NT
Những câu hỏi liên quan
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f’(x) và các khẳng định sau:(1). Hàm số yf(x) đồng biến trên khoảng
1
;
+
∞
(2). Hàm số yf(x) nghịch biến trên khoảng
-
∞
;
-
2
(3). Hàm số yf(x) nghịch biến trên khoảng
-...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
tìm các giá trị của m để hàm số
a) \(y=\dfrac{x+m}{x+1}\) nghịch biến trên từng khoảng xác định
b) \(y=\dfrac{2x-3m}{x-m}\) đồng biến trên từng khoảng xác định
a: TXĐ: D=R\{-1}
\(y'=\dfrac{\left(x+m\right)'\left(x+1\right)-\left(x+1\right)'\left(x+m\right)}{\left(x+1\right)^2}\)
\(=\dfrac{x+1-x-m}{\left(x+1\right)^2}=\dfrac{1-m}{\left(x+1\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\)
=>\(\dfrac{1-m}{\left(x+1\right)^2}< 0\)
=>1-m<0
=>m>1
b: TXĐ: D=R\{m}
\(y=\dfrac{2x-3m}{x-m}\)
=>\(y'=\dfrac{\left(2x-3m\right)'\left(x-m\right)-\left(2x-3m\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{2\left(x-m\right)-\left(2x-3m\right)}{\left(x-m\right)^2}=\dfrac{2x-2m-2x+3m}{\left(x-m\right)^2}\)
\(=\dfrac{m}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\)
=>\(\dfrac{m}{\left(x-m\right)^2}>0\)
=>m>0
Đúng 0
Bình luận (0)
Cho hàm số:
y
x
-
2
x
+
3
Khẳng định nào sau đây là đúng?A. Hàm số đồng biến trên từng khoảng xác định;B. Hàm số đồng biến trên khoảng (-
∞
;+
∞
);C. Hàm số nghịch biến trên từng khoảng xác định;D. Hàm số nghịch biến trên...
Đọc tiếp
Cho hàm số: y = x - 2 x + 3
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
Một học sinh khảo sát sự biến thiên của hàm số như sau:I. Tập xác định:
D
ℝ
II. Sự biến thiên:
y
x
2
−
x
−
2
;
y
0
⇔
x
−
1
x...
Đọc tiếp
Một học sinh khảo sát sự biến thiên của hàm số như sau:
I. Tập xác định: D = ℝ
II. Sự biến thiên: y ' = x 2 − x − 2 ; y ' = 0 ⇔ x = − 1 x = 2
lim x → − ∞ y = − ∞ ; lim x → + ∞ y = + ∞
III. Bảng biến thiên:
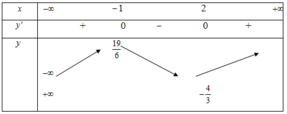
IV. Vậy hàm số đồng biến trên nghịch biến trên khoảng
−
∞
;
−
1
∪
2
;
+
∞
, nghịch biến trên khoảng
−
1
;
2
Lời giải trên sai từ bước nào?
A. Bước IV
B. Bước I
C. Bước II
D. Bước III
Đáp án là D.
• Sai ở bước III (bảng biến thiên)
Đúng 0
Bình luận (0)
tìm các giá trị của m để hàm số
a) \(y=\dfrac{2m-x}{x-3}\) đồng biến trên từng khoảng xác định
b) \(y=\dfrac{x+3}{x+m}\) nghịch biến trên từng khoảng xác định
a: TXĐ: D=R\{3}
\(y=\dfrac{2m-x}{x-3}\)
=>\(y'=\dfrac{\left(2m-x\right)'\left(x-3\right)-\left(2m-x\right)\left(x-3\right)'}{\left(x-3\right)^2}\)
\(=\dfrac{-\left(x-3\right)-2m+x}{\left(x-3\right)^2}\)
\(=\dfrac{3-2m}{\left(x-3\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì y'>0 với mọi x thỏa mãn ĐKXĐ
=>\(\dfrac{3-2m}{\left(x-3\right)^2}>0\)
=>3-2m>0
=>2m<3
=>\(m< \dfrac{3}{2}\)
b: TXĐ: D=R\{-m}
\(y=\dfrac{x+3}{x+m}\)
=>\(y'=\dfrac{\left(x+3\right)'\left(x+m\right)-\left(x+3\right)\left(x+m\right)'}{\left(x+m\right)^2}\)
\(=\dfrac{x+m-x-3}{\left(x+m\right)^2}=\dfrac{m-3}{\left(x+m\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\in TXĐ\)
=>\(\dfrac{m-3}{\left(x+m\right)^2}< 0\)
=>m-3<0
=>m<3
Đúng 0
Bình luận (0)
a) Quan sát đồ thị hàm số bậc hai y {x^2} + 2x - 3 trong Hình 11. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.b) Quan sát đồ thị hàm số bậc hai y - {x^2} + 2x + 3 trong Hình 12. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
Đọc tiếp
a) Quan sát đồ thị hàm số bậc hai \(y = {x^2} + 2x - 3\) trong Hình 11. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
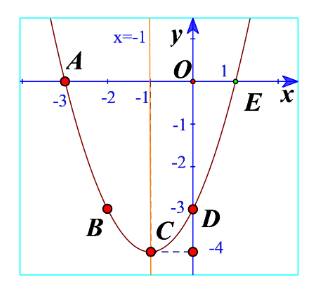
b) Quan sát đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) trong Hình 12. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
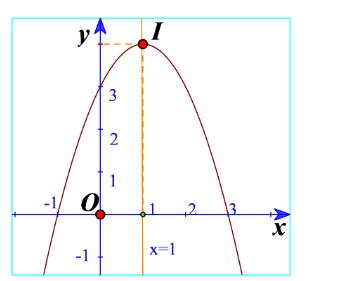
a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
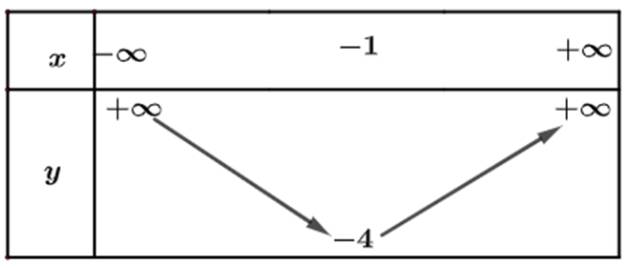
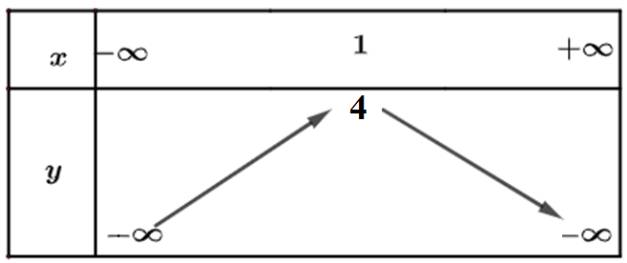
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
Đúng 0
Bình luận (0)
Cho hàm số yx5−5xyx^5-5xyx5−5x. Trong các khẳng định sau đây, khẳng định nào đúng?Hàm số đã cho nghịch biến trên nửa khoảng (−∞;1](-infty;1](−∞;1] và đồng biến trên nửa khoảng [1;+∞)[1;+infty)[1;+∞).Hàm số đã cho nghịch biến trên mỗi nửa khoảng (−∞;−1](-infty;-1](−∞;−1], [1;+∞)[1;+infty)[1;+∞) và đồng biến trên khoảng(−1;1)left(-1;1right)(−1;1).Hàm số đã cho đồng biến trên mỗi nửa khoảng (−∞;−1](-infty;-1](−∞;−1]; [1;
Đọc tiếp
Cho hàm số . Trong các khẳng định sau đây, khẳng định nào đúng?
Hàm số đã cho nghịch biến trên nửa khoảng và đồng biến trên nửa khoảng .Hàm số đã cho nghịch biến trên mỗi nửa khoảng , và đồng biến trên khoảng.Hàm số đã cho đồng biến trên mỗi nửa khoảng ;Xác định tham số m để hàm số sau:
a) 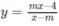 đồng biến trên từng khoảng xác định;
đồng biến trên từng khoảng xác định;
b) y = − x 3 + m x 2 − 3x + 4 nghịch biến trên.
a) Tập xác định: D = R \ {m}
Hàm số đồng biến trên từng khoảng ( - ∞ ; m), (m; + ∞ ) khi và chỉ khi:
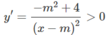
⇔ − m 2 + 4 > 0
⇔ m 2 < 4 ⇔ −2 < m < 2
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′ = −3 x 2 + 2mx – 3 ≤ 0
⇔ y′ = m 2 – 9 ≤ 0
⇔ m 2 ≤ 9 ⇔ −3 ≤ m ≤ 3
Đúng 0
Bình luận (0)
Xác định m để hàm số sau :
a) ydfrac{mx-4}{x-m} đồng biến trên từng khoảng xác định
b) ydfrac{-mx-5m+4}{x+m} nghịch biến trên từng khoảng xác định
c) y-x^3+mx^2-3x+4 nghịch biến trên left(-infty;+inftyright)
d) yx^3-2mx^2+12x-7 đồng biến trên mathbb{R}
Đọc tiếp
Xác định m để hàm số sau :
a) \(y=\dfrac{mx-4}{x-m}\) đồng biến trên từng khoảng xác định
b) \(y=\dfrac{-mx-5m+4}{x+m}\) nghịch biến trên từng khoảng xác định
c) \(y=-x^3+mx^2-3x+4\) nghịch biến trên \(\left(-\infty;+\infty\right)\)
d) \(y=x^3-2mx^2+12x-7\) đồng biến trên \(\mathbb{R}\)
a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3
Đúng 0
Bình luận (0)





