\(A=-x^2-5\)

Vì \(-x^2\le0\Leftrightarrow-x^2-5\le-5\)

Vậy \(A_{max}=-5\Leftrightarrow x=0\)

x=0

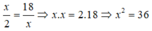
Suy ra, x = - 6 hoặc x = 6

Chọn đáp án C

a: Ta có: \(A=2x^2+12x+11\)

\(=2\left(x^2+6x+\dfrac{11}{2}\right)\)

\(=2\left(x^2+6x+9-\dfrac{7}{2}\right)\)

\(=2\left(x+3\right)^2-7\ge-7\forall x\)

Dấu '=' xảy ra khi x=-3

\(A=2\left(x^2+6x+36\right)-61=2\left(x+6\right)^2-61\ge-61\\ A_{min}=-61\Leftrightarrow x=-6\\ B=-\left(x^2-18x+81\right)+100=-\left(x-9\right)^2+100\le100\\ B_{max}=100\Leftrightarrow x=9\)

a: Ta có: \(2x^3-18x=0\)

\(\Leftrightarrow2x\left(x-3\right)\left(x+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)

b: Ta có: \(\left(3x-2\right)\left(2x+1\right)-6x\left(x+2\right)=11\)

\(\Leftrightarrow6x^2+3x-4x-2-6x^2-12x=11\)

\(\Leftrightarrow-13x=13\)

hay x=-1

c: Ta có: \(\left(x-1\right)^3-\left(x+2\right)\left(x^2-2x+4\right)=3\left(1-x^2\right)\)

\(\Leftrightarrow x^3-3x^2+3x-1-x^3-8=3-3x^2\)

\(\Leftrightarrow3x=12\)

hay x=4

a) 2x³-18x=0

⇔ 2x(x²-9)=0

⇔ 2x(x-3)(x+3)=0

⇔ \(\left\{{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)

b)(3x-1)(2x+1)-6x(x+2)=11

⇔ 6x²+x-1-6x²-12x=11

⇔ -11x=12

\(\Leftrightarrow x=-\dfrac{12}{11}\)

c) (x-1)³-(x+2).(x²-2x+4)=3.(1-x²)

⇔ x³-3x²+3x-1-x³-8-3+3x²=0

⇔ 3x=12

⇔   x=4

c. (x - 1)³ - (x + 2)(x² - 2x + 4) = 3(1 - x²)

<=> (x³ - 3x² + 3x - 1) - (x³ - 2x² + 4x + 2x² - 4x + 8) = 3 - 3x²

<=> x³ - 3x² + 3x - 1 - x³ + 2x² - 4x - 2x² + 4x - 8 = 3 - 3x²

<=> x³ - x³ - 3x² + 2x² - 2x² + 3x² + 3x - 4x + 4x = 3 + 1 + 8

<=> 3x = 12

<=> x = 4

1.

\(G=\dfrac{2}{x^2+8}\le\dfrac{2}{8}=\dfrac{1}{4}\)

\(G_{max}=\dfrac{1}{4}\) khi \(x=0\)

\(H=\dfrac{-3}{x^2-5x+1}\) biểu thức này ko có min max

2.

\(D=\dfrac{2x^2-16x+41}{x^2-8x+22}=\dfrac{2\left(x^2-8x+22\right)-3}{x^2-8x+22}=2-\dfrac{3}{\left(x-4\right)^2+6}\ge2-\dfrac{3}{6}=\dfrac{3}{2}\)

\(D_{min}=\dfrac{3}{2}\) khi \(x=4\)

\(E=\dfrac{4x^4-x^2-1}{\left(x^2+1\right)^2}=\dfrac{-\left(x^4+2x^2+1\right)+5x^4+x^2}{\left(x^2+1\right)^2}=-1+\dfrac{5x^4+x^2}{\left(x^2+1\right)^2}\ge-1\)

\(E_{min}=-1\) khi \(x=0\)

\(G=\dfrac{3\left(x^2-4x+5\right)-5}{x^2-4x+5}=3-\dfrac{5}{\left(x-2\right)^2+1}\ge3-\dfrac{5}{1}=-2\)

\(G_{min}=-2\) khi \(x=2\)

Với mọi số thực không âm a, b ta luôn có:

\(\left(a-b\right)^2\ge0\Leftrightarrow2ab\le a^2+b^2\)

\(\Leftrightarrow a^2+2ab+b^2\le2\left(a^2+b^2\right)\)

\(\Leftrightarrow\left(a+b\right)^2\le2\left(a^2+b^2\right)\)

\(\Leftrightarrow a+b\le\sqrt{2\left(a^2+b^2\right)}\)

Áp dụng:

a.

\(\sqrt{x-5}+\sqrt{23-x}\le\sqrt{2\left(x-5+23-x\right)}=6\)

Dấu "=" xảy ra khi \(x=14\)

b.

\(\sqrt{x-3}+\sqrt{19-x}\le\sqrt{2\left(x-3+19-x\right)}=4\sqrt{2}\)

Dấu "=" xảy ra khi \(x=11\)

$A=x^2+y^2-6x+4y+20=(x^2-6x+9)+(y^2+4y+4)+7$

$=(x-3)^2+(y+2)^2+7\geq 0+0+7=7$
Vậy $A_{\min}=7$. Giá trị này đạt tại $(x-3)^2=(y+2)^2=0$

$\Leftrightarrow x=3; y=-2$

---------------------

$B=9x^2+y^2+2z^2-18x+4z-6y+30$

$=(9x^2-18x+9)+(y^2-6y+9)+(2z^2+4z+2)+10$

$=9(x^2-2x+1)+(y^2-6y+9)+2(z^2+2z+1)+10$

$=9(x-1)^2+(y-3)^2+2(z+1)^2+10\geq 10$
Vậy $B_{\min}=10$. Giá trị này đạt tại $(x-1)^2=(y-3)^2=(z+1)^2$

$\Leftrightarrow x=1; y=3; z=-1$

$C=x^2+y^2+z^2-xy-yz-xz+3$

$2C=2x^2+2y^2+2z^2-2xy-2yz-2xz+6$

$=(x^2-2xy+y^2)+(y^2-2yz+z^2)+(x^2-2xz+z^2)+6$

$=(x-y)^2+(y-z)^2+(z-x)^2+6\geq 6$

$\Rightarrow C\geq 3$

Vậy $C_{\min}=3$. Giá trị này đạt tại $x-y=y-z=z-x=0$

$\Leftrihgtarrow x=y=z$

--------------------------------------

$D=5x^2+2y^2+4xy-2x+4y+2021$

$=2(y^2+2xy+x^2)+3x^2-2x+4y+2021$

$=2(x+y)^2+4(x+y)+3x^2-6x+2021$
$=2(x+y)^2+4(x+y)+2+3(x^2-2x+1)+2016$

$=2[(x+y)^2+2(x+y)+1]+3(x^2-2x+1)+2016$

$=2(x+y+1)^2+3(x-1)^2+2016\geq 2016$

Vậy $D_{\min}=2016$ khi $x+y+1=x-1=0$

$\Leftrightarrow x=1; y=-2$

$E=x^2-2x+4y^2+4y+2014$

$=(x^2-2x+1)+(4y^2+4y+1)+2012$

$=(x-1)^2+(2y+1)^2+2012$

$\geq 2012$

Vậy $E_{\min}=2012$. Giá trị này đạt tại $x-1=2y+1=0$

$\Leftrightarrow x=1; y=\frac{-1}{2}$

----------------------

$F=5x^2+5y^2+8xy+2y-2x+30$

$=4(x^2+2xy+y^2)+x^2+y^2+2y-2x+30$

$=4(x+y)^2+(x^2-2x+1)+(y^2+2y+1)+28$

$=4(x+y)^2+(x-1)^2+(y+1)^2+28\geq 28$

Vậy $F_{\min}=28$. Giá trị này đạt tại $x+y=x-1=y+1=0$

$\Leftrightarrow x=1; y=-1$