Chứng minh biểu thức sau luôn có giá trị dương với mọi x
a) C = 3x2 + 4x + 7
b) D = 2x2 - 5x + 5
Chứng minh rằng các biểu thức sau luôn nhận giá trị dương với mọi giá trị của biến.
a) x2 - 5x +10
b) 2x2 + 8x +15
c) (x-1).(x-2) + 5
d) (x+5).(x-3) + 20
Mọi người giúp mình với :<
a: \(x^2-5x+10\)
\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{15}{4}\)
\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{15}{4}>0\forall x\)
b: \(2x^2+8x+15\)
\(=2\left(x^2+4x+\dfrac{15}{2}\right)\)
\(=2\left(x^2+4x+4+\dfrac{7}{2}\right)\)
\(=2\left(x+2\right)^2+7>0\forall x\)
Bài 1:chứng minh các biểu thức luôn nhận giá trị dương với mọi x:
a)E=4x^2+6x+5. b)F=2x^2-3x+7
c)K=5x^2-4x+1. d)Q=3x^2+2x+5
a.chứng minh rằng biểu thức P=5x(2-x)-(x+1)(x+9) luôn nhận giá trị âm với mọi giá trị của biến x.
b. chứng minh rằng biểu thức Q=3x2+x(x-4y)-2x(6-2y)+12x+1 luôn nhận giá trị dương với mọi giá trị của biến x và y
\(a,P=5x\left(2-x\right)-\left(x+1\right)\left(x+9\right)\)
\(=10x-5x^2-\left(x^2+x+9x+9\right)\)
\(=10x-5x^2-x^2-x-9x-9\)
\(=\left(10x-x-9x\right)+\left(-5x^2-x^2\right)-9\)
\(=-6x^2-9\)
Ta thấy: \(x^2\ge0\forall x\)
\(\Rightarrow-6x^2\le0\forall x\)
\(\Rightarrow-6x^2-9\le-9< 0\forall x\)
hay \(P\) luôn nhận giá trị âm với mọi giá trị của biến \(x\).
\(b,Q=3x^2+x\left(x-4y\right)-2x\left(6-2y\right)+12x+1\)
\(=3x^2+x^2-4xy-12x+4xy+12x+1\)
\(=\left(3x^2+x^2\right)+\left(-4xy+4xy\right)+\left(-12x+12x\right)+1\)
\(=4x^2+1\)
Ta thấy: \(x^2\ge0\forall x\)
\(\Rightarrow4x^2\ge0\forall x\)
\(\Rightarrow4x^2+1\ge1>0\forall x\)
hay \(Q\) luôn nhận giá trị dương với mọi giá trị của biến \(x\) và \(y\).
#\(Toru\)
Bài 1: Chứng minh các biểu thức sau luôn dương với mọi x:
a) 9x2 - 6x + 11
b) 3x2 - 12x + 81
c) 5x2 - 5x + 4
d) 2x2 - 2x + 9
a) \(9x^2-6x+11=\left(3x\right)^2-2.3x+1+10=\left(3x-1\right)^2+10>0\forall x\)
b) \(3x^2-12x+81=3.\left(x^2-4x+9\right)=3.\left(x-2\right)^2+15>0\forall x\)
c) \(5x^2-5x+4=5.\left(x^2-x+\dfrac{4}{5}\right)=5.\left(x^2-x+\dfrac{1}{4}+\dfrac{11}{20}\right)=5.\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall x\)
d) \(2x^2-2x+9=2.\left(x^2-x+\dfrac{9}{2}\right)=2.\left(x-\dfrac{1}{2}\right)^2+\dfrac{17}{2}>0\forall x\)
a) = (3x-1)^2+10
Do (3x-1)^2>=0 với mọi x
--> (3x-1)^2+10>0 với mọi x
a) \(9x^2-6x+11=\left(3x-1\right)^2+10\ge10>0\)
b) \(3x^2-12x+81=3\left(x-2\right)^2+69\ge69>0\)
c) \(5x^2-5x+4=5\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}>0\)
d) \(2x^2-2x+9=2\left(x-\dfrac{1}{2}\right)^2+\dfrac{17}{2}\ge\dfrac{17}{2}>0\)
Chứng minh các biểu thức sau luôn dương với mọi giá trị của biến
a,x^2-4x-7
b,4x^2-12x+11
c,x^2-x+1
Câu hỏi của ĐỖ THỊ HƯƠNG TRÀ - Toán lớp 8 - Học trực tuyến OLM
mình làm rồi nhé, bạn kham khảo link
Chú ý rằng nếu c > 0 thì a + b 2 + c và a + b 2 + c đều dương với mọi a, b. Áp dụng điều này chứng minh rằng:
Với mọi giá trị của x khác 0 và khác – 3, biểu thức:
1 - x 2 x . x 2 x + 3 - 1 + 3 x 2 - 14 x + 3 x 2 + 3 x luôn luôn có giá trị âm.
Điều kiện x ≠ 0 và x ≠ -3
Ta có:
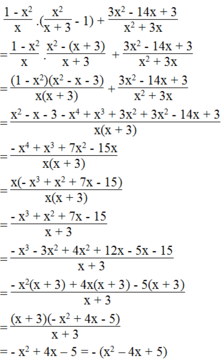
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3
Cho biểu thức M = (2x-3)^2-x(3-x)+5x-4x^2+17
a)rút gọn biểu thức M
b)chứng minh giá trị biểu thức M luôn giá trị dương với mọi x
`#3107.\text {DN}`
a)
\((2x-3)^2-x(3-x)+5x-4x^2+17\)
`= 4x^2 - 12x + 9 - 3x + x^2 + 5x - 4x^2 + 17`
`= x^2 - 10x + 26`
b)
`M = x^2 - 10x + 26`
`= [(x)^2 - 2*x*5 + 5^2] + 1`
`= (x - 5)^2 + 1`
Vì `(x - 5)^2 \ge 0` `AA` `x => (x - 5)^2 + 1 \ge 1` `AA` `x`
Vậy, giá trị biểu thức M luôn có giá trị dương với mọi x.
Bài 1:Chứng minh các biểu thức luôn nhạn giá trị dương với mọi x:
a)E=4x^2+6x+5. b)F=2x^2-3x+7
c)K=5x^2-4x+1. d)Q=3x^2+2x+5
GIÚP MÌNH GẤP CÁI.THANK NHA
a, \(E=4x^2+6x+5=4\left(x^2+\frac{2.3}{4}x+\frac{9}{16}-\frac{9}{16}\right)+5\)
\(=4\left(x+\frac{3}{4}\right)^2+\frac{11}{4}\ge\frac{11}{4}>0\forall x\)
Vậy ta có đpcm
b, \(F=2x^2-3x+7=2\left(x^2-\frac{2.3}{4}x+\frac{9}{16}-\frac{9}{16}\right)+7\)
\(=2\left(x-\frac{3}{4}\right)^2+\frac{47}{8}\ge\frac{47}{8}>0\forall x\)
Vậy ta có đpcm
c, \(K=5x^2-4x+1=5\left(x^2-\frac{2.2}{5}x+\frac{4}{25}-\frac{4}{25}\right)+1\)
\(=5\left(x-\frac{2}{5}\right)^2+\frac{1}{5}\ge\frac{1}{5}>0\forall x\)
Vậy ta có đpcm
d, \(Q=3x^2+2x+5=3\left(x^2+\frac{2}{3}x+\frac{1}{9}-\frac{1}{9}\right)+5\)
\(=3\left(x+\frac{1}{3}\right)^2+\frac{14}{3}\ge\frac{14}{3}>0\forall x\)
Vậy ta có đpcm
Chứng minh các biểu thức sau luôn có giá trị dương với mọi giá trị của biến: a) 1/4 x -x² +2 b) 3x + 2x² +1 c) 9x² -12x + 5 d) ( x+2)² +(x-2)²
a: Sửa đề: 1/4x+x^2+2
x^2+1/4x+2
=x^2+2*x*1/8+1/64+127/64
=(x+1/8)^2+127/64>=127/64>0 với mọi x
=>ĐPCM
b: 2x^2+3x+1
=2(x^2+3/2x+1/2)
=2(x^2+2*x*3/4+9/16-1/16)
=2(x+3/4)^2-1/8
Biểu thức này ko thể luôn dương nha bạn
c: 9x^2-12x+5
=9x^2-12x+4+1
=(3x-2)^2+1>=1>0 với mọi x
d: (x+2)^2+(x-2)^2
=x^2+4x+4+x^2-4x+4
=2x^2+8>=8>0 với mọi x
Bài1:chứng minh các biểu thức luôn nhận giá trị âm với mọi x:
a)A=-x^2+2x-3. b)C=-x^2+4x-7
c)D=-2x^2-6x-5. d)E=-3x^2+4x-4
e)F=-5x^2-3x-5
a, \(A=-x^2+2x-3=-\left(x^2-2x+1-1\right)-3=-\left(x-1\right)^2-2\le-2< 0\forall x\)
Vậy ta có đpcm
b, \(C=-x^2+4x-7=-\left(x^2-4x+4-4\right)-7=-\left(x-2\right)^2-3\le-3< 0\forall x\)
Vậy ta có đpcm
c, \(D=-2x^2-6x-5=-2\left(x^2+\frac{2.3}{2}x+\frac{9}{4}-\frac{9}{4}\right)-5\)
\(=-2\left(x+\frac{3}{2}\right)^2-\frac{1}{2}\le-\frac{1}{2}< 0\forall x\)
Vậy ta có đpcm
d, \(E=-3x^2+4x-4=-3\left(x^2-\frac{4}{3}x+\frac{4}{9}-\frac{4}{9}\right)-4\)
\(=-3\left(x-\frac{2}{3}\right)^2-\frac{8}{3}\le-\frac{8}{3}< 0\forall x\)
Vậy ta có đpcm
e, tự làm nhé