3 x 3 + 2 x 2 − 7 x   + a : 3 x − 1 = 3 x 3 − x 2 + 3 x 2 − x − 6 x + 2 − 2 + a : 3 x − 1 = x 2 3 x − 1 + x 3 x − 1 − 2 3 x − 1 + a − 2 : 3 x − 1 = x 2 + x − 2 3 x − 1 + a − 2 : 3 x − 1

Đa thức 3 x 3 + 2 x 2 − 7 x   + a chia hết cho đa thức 3 x - 1 khi và chỉ khi a − 2 = 0 ⇒ a = 2 .

\(a,\Leftrightarrow4x^3-2x^2+a=\left(2x-3\right).a\left(x\right)\)

Thay \(x=\dfrac{3}{2}\Leftrightarrow4.\dfrac{27}{8}-2.\dfrac{9}{4}+a=0\)

\(\Leftrightarrow\dfrac{27}{2}-\dfrac{9}{2}+a=0\\ \Leftrightarrow a=-9\)

\(b,\Leftrightarrow3x^3+2x^2+x+a=\left(x+1\right).b\left(x\right)+2\)

Thay \(x=-1\Leftrightarrow-3+2-1+a=2\Leftrightarrow a=4\)

Thực hiện phép chia đa thức, ta có:

\(3x^3+2x^2-7x+a=\left(3x-1\right).\left(x^2+x-2\right)+a-2\)

Để đa thức \(3x^3+2x^2-7x+a\)chia hết cho đa thức 3x-1  thì a-2=0=> a=2

Đặt \(f\left(x\right)=3x^3+2x^2-7x+a\)

Áp dụng định lý Bezout:

\(f\left(x\right)=3x^3+2x^2-7x+a\)chia hết cho đa thức 3x - 1

\(\Leftrightarrow f\left(\frac{1}{3}\right)=0\)

\(\Leftrightarrow3.\left(\frac{1}{3}\right)^3+2.\left(\frac{1}{3}\right)^2-7.\frac{1}{3}+a=0\)

\(\Leftrightarrow\frac{1}{9}+\frac{2}{9}-\frac{7}{3}+a=0\)

\(\Leftrightarrow\frac{1}{3}-\frac{7}{3}+a=0\)

\(\Leftrightarrow-2+a=0\)

\(\Leftrightarrow a=2\)

Vậy a = 2 thì ​​​\(f\left(x\right)=3x^3+2x^2-7x+a\)​chia hết cho đa thức 3x - 1
 

a: 3x^3+2x^2-7x+a chia hêt cho 3x-1

=>3x^3-x^2+3x^2-x-6x+2+a-2 chia hết cho 3x-1

=>a-2=0

=>a=2

c: =>2x^2-6x+(a+6)x-3a-18+3a+19 chia x-3 dư 4

=>3a+19=4

=>3a=-15

=>a=-5

d: 2x^3-x^2+ax+b chiahêt cho x^2-1

=>2x^3-2x-x^2+1+(a+2)x+b-1 chia hết cho x^2-1

=>a+2=0 và b-1=0

=>a=-2 và b=1

Lời giải

Ta có

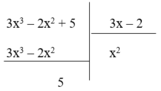
Vì phần dư R = 5 ≠ 0 nên phép chia đa thức 3 x 3   –   2 x 2 + 5 cho đa thức 3x – 2 là phép chia có dư. Do đó (I) sai

Lại có

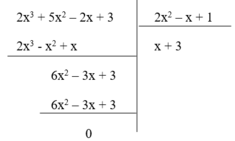
Nhận thấy phần dư R = 0 nên phép chia đa thức ( 2 x 3   +   5 x 2 – 2x + 3) cho đa thức (2 x 2 – x + 1) là phép chia hết. Do đó (II) đúng

Đáp án cần chọn là: D

b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)

\(=2x^2-3x+1\)

Cho g(x) = 0

x + 1 = 0

x = -1

Để f(x) chia hết cho g(x) thì x = -1 cũng là nghiệm của f(x)

Hay f(1) = 0

3.1² + 2.1² - 7.1 - m + 2 = 0

-2 - m + 2 = 0

m = 0

Vậy m = 0 thì f(x) chia hết cho g(x)

Giải chi tiết của em đây :

F(x) = 3x² + 2x² - 7x - m + 2 

F(x) \(⋮\) x + 1 \(\Leftrightarrow\) F(x) \(⋮\) x - (-1)

Theo bezout ta có : F(x) \(⋮\) x - (-1) \(\Leftrightarrow\) F(-1) = 0

\(\Leftrightarrow\) 3(-1)² + 2(-1)² - 7.(-1) - m + 2 = 0

    3 + 2 + 7 - m + 2 =0

              14 - m = 0

                     m = 14

Kết luận với m = 14 thì F(x) chia hết cho x + 1 

Theo định lý Bezout, ta có:

2x^2+5x+a chia hết cho x + 1

--> 2.(-1)^2 + 5.(-1)+a = 0

--> a = 3

\(2x^2+5x+a⋮x+1\)

\(\Leftrightarrow a-3=0\)

hay a=3

a: Khi x=-1 thì B=2*(-1)^2+1+1=4

b: Để A chia hết cho B thì 

\(2x^3-x^2+x+6x^2-3x+3+a-3⋮2x^2-x+1\)

=>a-3=0

=>a=3

c: Để B=1 thì 2x^2-x=0

=>x=0 hoặc x=1/2