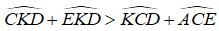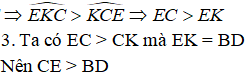đặt thừa số chung rồi đơn giản biểu thức: ab-bd-be+ce+cd+ae
TH
Những câu hỏi liên quan
đặt thừa số chung rồi rút gọn biểu thức A= (ab - ad).(ba+ad)/(bc+cd).(bc - cd) và (c khác 0 , b khác +d và -d)
rút gọn
ab-bd-be+ce+cd+ae
1. Cho sáu điểm A,B,C,D,E,F. Chứng minh :
a) AB+BC+CD+DA=0
b) AB+DC+BD+CA=0
c) CD+BC+AB=AD
d) AB+CD=AD+CB
e) AD+BE+CF=AE+BF+CD=AF+BD+CE
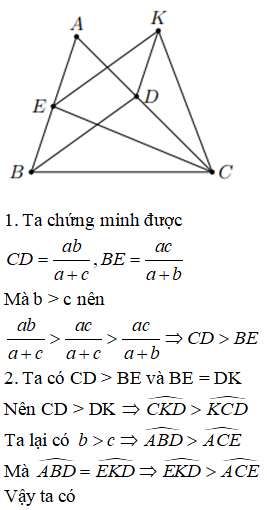
Bài 23/ Cho tam giác ABC có BC = a, AC = b, AB = c (b > c), các đường phân giác BD,
CE.
a) Tính các độ dài CD, BE rồi suy ra CD > BE
b) Vẽ hình bình hành BEKD. Chứng minh CE > EK
c) Chứng minh CE > BD.
Cho ABC có BC = a, AC = b, AB = c (b > c), các phân giác BD, CE
a) Tính độ dài CD, BE rồi suy ra CD > BE
b) Vẽ hình bình hành BEKD. Chứng minh: CE > EK
c) Chứng minh CE > BD
Cho tam giác ABC . Gọi M là trung điểm của BC . Quá B và C lần lượt kẻ BD và CE vuông góc với đường thẳng AM a. Chứng minh BD= CE và BD // CE b. Chứng minh BE // CD và BE = CD c. Chứng minh AD + AE = 2AM
a: Xét ΔBMD vuông tại D và ΔCME vuông tại E có
MB=MC
\(\widehat{BMD}=\widehat{CME}\)(hai góc đối đỉnh)
Do đó: ΔBMD=ΔCME
=>BD=CE
Ta có: BD\(\perp\)AM
CE\(\perp\)AM
Do đó: BD//CE
b: Xét tứ giác BDCE có
BD//CE
BD=CE
Do đó: BDCE là hình bình hành
=>BE//CD và BE=CD
c: \(AD+AE=AD+AD+DE\)
\(=2AD+2DM\)
\(=2\left(AD+DM\right)=2AM\)
Đúng 1
Bình luận (1)
Các bạn giu`p mình kiếm tra và làm lại bài này nhé, cảm ơn nhiềuĐề : Bài 1: Cho tam giác ABC vuông tại A. BD là đường trung tuyến . Kẻ DE vuông góc với bc tại E.A. Chứng minh BE2 + CE2BD2 - CD2b. Chứng minh AB2 BE2 - CE2Giải: a. Xét tam giác ABD và ABD có :Góc A Góc E 90 độ ( gt)BD chung Hai tam giác bằng nhau AD AE ( cạnh tương ứng )mà BD là đường trung tuyến của tam giác ABC ADCD) DEDC Vì ABD TAM GIÁC EBD BE BD BE^2-CE^2BD^2-CD^2B. Ta có E thuộc Bc BCBE+ECmà ABBE AB BC - CE AB^2 BC...
Đọc tiếp
Các bạn giu`p mình kiếm tra và làm lại bài này nhé, cảm ơn nhiều
Đề :
Bài 1: Cho tam giác ABC vuông tại A. BD là đường trung tuyến . Kẻ DE vuông góc với bc tại E.
A. Chứng minh BE2 + CE2=BD2 - CD2
b. Chứng minh AB2 = BE2 - CE2
Giải: a. Xét tam giác ABD và ABD có :
Góc A = Góc E = 90 độ ( gt)
BD chung
=> Hai tam giác bằng nhau
=> AD = AE ( cạnh tương ứng )
mà BD là đường trung tuyến của tam giác ABC => AD=CD
=) DE=DC
Vì ABD = TAM GIÁC EBD => BE = BD
=> BE^2-CE^2=BD^2-CD^2
B. Ta có E thuộc Bc
=> BC=BE+EC
mà AB=BE
=> AB = BC - CE
<=> AB^2 = BC^2 - CE^2
Bài 2 Cho tam giác ABC có ba góc nhọn có AH là đường cao. cHỨNG MINH : AB^2+CH^2=AC^2+BH^2
trong tam giac vuong ABH Cco \(AH^2+BH^2=AB^2\Rightarrow AH^2=AB^2-BH^2\left(1\right)\)
AHC co \(AH^2+HC^2=AC^2\Rightarrow AH^2=AC^2-HC^2\left(2\right)\)
tu (1) va(2 ) suy ra \(AB^2-BH^2=AC^2-HC^2\Rightarrow AB^2+HC^2=AC^2+BH^2\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC=a,AC=b,AB=c(b>c), các phân giác BD,CE
a, Tính CD,BE rồi suy ra CD>BE
b, Vẽ hình bình hành BEKD. CM: CE>EK
c, CM: CE>BD
Cho tam giác ABC có BC=a, AC=b, AB=c (b>c). các phân giác BD, CE.
a. Tính độ dài CD, BE rồi suy ra CD>BE.
b. Vẽ hình bình hành BEKD . Chứng minh CE>EK.
c. Chứng minh CE>BD.