Ai cho mình biết định lý py ta go hộ mình với
LV
Những câu hỏi liên quan

Giúp mình với ạ mình chx học định lý py-ta-go nên mn đừng làm cách liên quan đến nó nhs
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
Đúng 0
Bình luận (1)
Thế nào là định lý Py-ta-go và nội dung ghi nhớ
Giúp mình với các bạn ơi♫♪☼
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
∆ABC vuông tại A.
Xem thêm tại: https://loigiaihay.com/ly-thuyet-dinh-li-pytago-c42a5134.html#ixzz5ZC9Zwx7W
nhớ k mk nha ^_^
Đúng 0
Bình luận (0)
Bài làm
1. Định lì Pytago
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
∆ABC vuông tại A.
=> BC2=AB2+AC2
2. Định lí Pytago đảo.
Nếu một tam giác có bình phương của một cạnh bẳng tổng bình phương các cạnh còn lại thì tam giác đó là tam giác vuông.
∆ABC :BC2=AB2+AC2
=> ˆBACBAC^= 902
# Chúc bạn học tốt #
Đúng 0
Bình luận (0)
Py-ta-go là bình phương cạnh huyền bằng tổng bình phương 2 cạnh còn lại
Bạn chỉ cần nhớ
ch\(^2\)= (c1+c2)\(^2\)
Đúng 0
Bình luận (0)
Có ai biết đề các bài tập ở phần Bài Tập sách giáo khoa bài Định lý Pi-ta-go ko. Cho mình đề với. Mình bị người khác cầm sách về rồi.
bài thầy cô giao mỗi trường khác nhau nên mik cx k bik nữa >_<
Đúng 0
Bình luận (0)
Có ai biết đề các bài tập ở phần Bài Tập sách giáo khoa bài Định lý Pi-ta-go ko. Cho mình đề với. Mình bị người khác cầm sách về rồi.
Xem thêm câu trả lời
1.Hãy chọn 2 chữ số sao cho có thể viết hai chữ số đó dưới dạng 1 lũy thừa để được kết quả là số nguyên dương nhỏ nhất .
2. Định lý Py-ta-go là gì ?
3 Hàm số là gì ?
( Ai nhanh nhất mình tích )
Câu 1.
Ta có số nguyên dương nhỏ nhất là 1 nên:
\(1^1=1^2=1^3=1^4=1^5=1^6=1^7=1^8=1^9=1\)
\(1^0=2^0=3^0=4^0=5^0=6^0=7^0=8^0=9^0=1\)
Câu 2.
Định lý Py - ta - go là Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Câu 3.
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
yên tâm đi anh này học giỏi hay học dốt chị k biết đâu OvO
Hình như chưa ai trả lời được ??
Xem thêm câu trả lời
Nêu định lý thuận và đảo của định lý Py-ta-go ?
Thuận:
Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông.
Đảo:
Tam giác có bình phương 1 cạnh bằng tổng bình phương 2 cạnh còn lại là tam giác vuông.
Có thể ko chính xác từng chữ (do lười học bài cũ), bạn thông cảm nhé ^^!
Đúng 0
Bình luận (0)
Thuận:
Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông
Đảo:
Trong một tam giác, nếu có bình phương một cạnh bẳng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông
Nếu mình nhớ ko nhầm thì hình như hai định lý được phát biểu như thế này. Nếu có gì sai xin các bạn thông cảm
Đúng 0
Bình luận (0)
Thuận:
Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông
Đảo:
Trong một tam giác, nếu có bình phương cạnh huyền bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông
nếu mình nhớ ko nhầm thì hai định lý đc phát biểu như thế, có gì sai thì xin bạn thông cảm ^^
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có đn-định-lý-py-ta-go
? đề bài
lag!!!! :D
mik ko hiểu đề bài nha
hok tốt
Việt
Chứng minh định lý Py-ta-go
Xếp các tam giác vuông = nhau như hình vẽ:
Ta có: \(S_{BCDE}=S_{AMPN}+4.S_{ABC}\)
\(\Rightarrow a^2=\left(c-d\right)^2+4.\frac{bc}{2}\)
\(\Leftrightarrow a^2=c^2-2.bc+b^2+2.bc\)
\(\Leftrightarrow a^2=c^2+b^2\)
P/s: Còn nhiều cách.
Đúng 0
Bình luận (0)
Đây cũng là một cách chứng minh được giới thiệu trong cuốn sách của Elisha Scott Loomis. Ann Condit nghĩ ra cách chứng minh này vào năm 1938 khi cô mới 16 tuổi và là sinh viên của trường trung học ở miền nam Ấn Độ.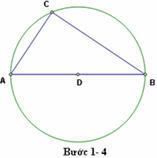
Dựng hình và kiểm tra
1. Dựng đoạn thẳng AB.
2. Vẽ trung điểm D của đoạn thẳng này
3. Vẽ đường tròn bán kính DA.
4. Vẽ đoạn BC và AC , với C là một điểm nằm trên đường tròn. Như vvậy ta đã dựng được tam giác vuông ABC vuông tại C.
5. Vẽ các hình vuông trên các cạnh của tam giác vuông ABC.
6. Vẽ các trung điểm L, M, N của các cạnh phía ngoài của các hình vuông.
7. Vẽ các đoạn DL, DM, DL.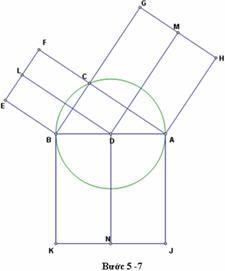
8. Vẽ đoạn FG, Vẽ tia DC, và điểm P là giao điểm cuat tia DC và đoạn FG, sau đó làm ẩn đi tia DC và hiện đoạn DP.
9. Tô màu khác nhau cho diện tích các tam giác DCF, DCG, và DBK.
Cách chứng minh này đưa ra mối liên quan giữa diện tích của các hình tam giác được tô màu với diện tích của các hình vuông trên các cạnh tam giác vuông.
Chọn menu Measure --> calculate để tính được tỉ lệ diện tích của các tam giác với các hình vuông tương ứng.
10. Đo diện tích các tam giác, và di chuyển điểm C quanh một nửa đường tròn trên đường kính AB.
Ta nhận thấy: tổng diện tích của 2 tam giác nhỏ luôn bằng diện tích của tam giác lớn hơn. Và tổng diện tích này không đổi khi điểm C chuyển động trên đường tròn. (xem hình bên dưới).
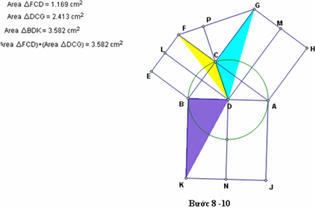
♥Trên mạng nha..Bn tham khảo nhé♥
Đúng 0
Bình luận (0)
Chỉ sd định lý Py ta go thôi ạ
Đọc tiếp
Chỉ sd định lý Py ta go thôi ạ
á đù biết làm rồi cho người ta làm chi tự làm giỏi chửi tui ông cũng vậy
Đúng 0
Bình luận (2)


