tĩm x
(x-1)(4-x)\(\ge\)0
Tĩm thuộc N biết: (x+4).(21-x)=0
(x + 4).(21 - x) = 0
=> x + 4 = 0 hoặc 21 - x = 0
Mà x + 4 = 0
=> x = -4
21 - x = 0
=> x = 21
Mà x thuộc N
=> x = 21
ngu nhể, chưa đok kĩ đề bài TT =="
Tĩm, biết
a, (x-5) (4-x) >0
b, x2 -2x lớn hơn hoặc bằng 0
a) \(\left(x-5\right)\left(4-x\right)>0\)
\(\Rightarrow\left\{{}\begin{matrix}x-5>0\\4-x>0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x>5\\x>4\end{matrix}\right.\)\(\Rightarrow x>5\)
\(\left\{{}\begin{matrix}x-5< 0\\4-x< 0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x< 5\\x< 4\end{matrix}\right.\)\(\Rightarrow x< 4\)
Tập nghiệm: x > 5 ; x < 4
b) \(x^2-2x\ge0\)
\(\Leftrightarrow x\left(x-2\right)\ge0\)
\(\Rightarrow\left\{{}\begin{matrix}x\ge0\\x-2\ge0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x\ge0\\x\ge2\end{matrix}\right.\)\(\Rightarrow x\ge2\)
\(\left\{{}\begin{matrix}x\le0\\x-2\le0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x\le0\\x\le2\end{matrix}\right.\)\(\Rightarrow x\le0\)
Tập nghiệm: x >= 2 ; x<= 0
Tĩm, biết : (1+3+5+...+101 )×x=0
Ta thấy: 1 + 3 + 5 + ... + 101 là 1 tổng các số nguyên dương, do đó nó luôn lớn hơn 0
Mà (1 + 3 + 5 + ... + 101) . x = 0
=> x = 0
Cách khác:
Tính tổng (1 + 3 + 5 + ... + 101):
Số số hạng của tổng là: (101 - 1) : 2 + 1 = 51 (số)
Tổng là: (101 + 1) . 51 : 2 = 2601
=> 2601 . x = 0
=> x = 0 : 2601
=> x = 0.
Cách nào cũng suy ra được x = 0 cả :))
=0 nhé bạn
có acc facebook thì ib làm quen
cho biểu thức y=x/(x+2013)2 vơi x>0
tĩm x để giá của biểu thức đạt giá trị lớn nhất. tĩm giá trị lớn nhất đó
1,Tìm GTNN biết
a,D=|x+1|+|x+3+|x+5|
2,Tĩm x biết
|x+2| -|3x-1|=0
2,
|x+2| - |3x-1| = 0
⇒\(\left[{}\begin{matrix}x+2=0\\3x-1=0\end{matrix}\right.\)⇒\(\left[{}\begin{matrix}x=-2\\3x=1\end{matrix}\right.\)⇒\(\left[{}\begin{matrix}x=-2\\x=1:3\end{matrix}\right.\)
⇒\(\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{3}\end{matrix}\right.\)
Vậy x ∈ \(\left\{\left(-2\right);\dfrac{1}{3}\right\}\)
1,
D= |x+1| + |x+3| + |x+5|
= |-x-1| + |x+3| + |x+5|
= |-x-1+x+3+x+5| = 1
Dấu bằng xảy ra khi -5 ≤ x ≤ -1
Vậy GTNN của D bằng 1 khi -5 ≤ x ≤ -1
Bài 1 mk lm bừa ko đúng đâu nha ☺
Tick mk bài 2 nhé
MẠI ZÔ MẠI ZÔ !!!
Tĩm x ; x-7/2<0
x - 7/2 < 0
cộng 2 vế x - 7/2 < 0 cho 7/2 ta được
=> x - 7/2 + 7/2 < 0 + 7/2
=> x < 7/2
vậy x < 7/2
x-7/2<0
cộng 2 vế x-7/2<0 cho 7/2 ta được
=>x-7/2+7/2<0+7/2
=>x<7/2
vậy x<7/2
sao các bạn lạ zạy Nguyễn Nam Cao copy mjk mà dc **** mjk thj ko có
Tĩm biết
a,x^2+3x=0
b,x^3-4x=0
a,x^2+3x=0
=> x.(x+3)=0
=> +)x=0
+) x+3=0 => x=-3
b,x^3-4x=0
=> x.(x^2-2^2)=0
=> x.(x-2).(x+2)=0
=> +) x=0
+) x-2=0 => x=2
+) x+2=0 => x= -2
a) \(x^2+3x=0\)
\(x\left(x+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x+3=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=-3\end{cases}}\)
vay \(\orbr{\begin{cases}x=0\\x=-3\end{cases}}\)
b) \(x^3-4x=0\)
\(x\left(x^2-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x^2-4=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x^2=4\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
vay \(\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
a) \(x^2+3x=0\)
\(x\left(x+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x+3=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x=-3\end{cases}}\)
Vậy \(x\in\left\{-3;0\right\}\)
b) \(x^3-4x\)
\(x\left(x^2-2^2\right)=0\)
\(x\left(x-2\right)\left(x+2\right)=0\)
=> x = 0
Hoặc x - 2 = 0 => x = 2
Hoặc x + 2 = 0 => x = -2
Vậy \(x\in\left\{-2;0;2\right\}\)
Giải các bất phương trình sau:
a) \(2{x^2} + 3x + 1 \ge 0\)
b) \( - 3{x^2} + x + 1 > 0\)
c) \(4{x^2} + 4x + 1 \ge 0\)
d) \( - 16{x^2} + 8x - 1 < 0\)
e) \(2{x^2} + x + 3 < 0\)
g) \( - 3{x^2} + 4x - 5 < 0\)
a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
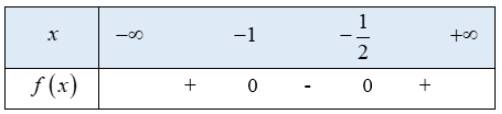
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
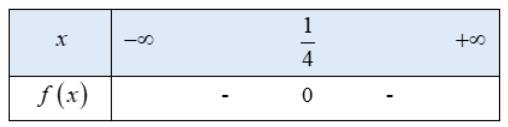
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)
HELPP MEE : Giari pt
a) (x-3)(x-2)<0
b) (x+3)(x+4)(x2+2)\(\ge\) 0
c) \(\dfrac{x-1}{x-2}\) \(\ge\)0
d)\(\dfrac{x+3}{2-x}\)\(\ge\) 0
e) (x-3)(x-2)(x+1)<0
g) \(\dfrac{2}{x-1}\)<0
k) x2 +3x+2>0
m) x2+1<0
a: (x-3)(x-2)<0
=>x-2>0 và x-3<0
=>2<x<3
b: \(\left(x+3\right)\left(x+4\right)\left(x^2+2\right)\ge0\)
=>(x+3)(x+4)>=0
=>x+3>=0 hoặc x+4<=0
=>x>=-3 hoặc x<=-4
c: \(\dfrac{x-1}{x-2}\ge0\)
=>x-2>0 hoặc x-1<=0
=>x>2 hoặc x<=1
d: \(\dfrac{x+3}{2-x}>=0\)
=>\(\dfrac{x+3}{x-2}< =0\)
=>x+3>=0 và x-2<0
=>-3<=x<2