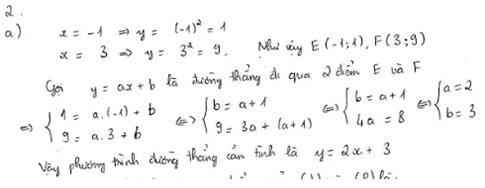Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TA
Những câu hỏi liên quan
trong mặt phẳng với hệ trục tọa độ oxy cho d đi qua A(3;7) và song song với đường thẳng có phương trình y= 3x+1
a) viết phương trình đt d
b) tìm tọa độ giao điểm đt d với parabol (P) : y = x2
Phần b mk chưa học nên chịu :v
a, Phương trình đường thẳng (d) là: y = ax + b
Vì đường thẳng (d) song song với đường thẳng y = 3x + 1 nên
\(\Rightarrow\) \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=3\\b\ne1\end{matrix}\right.\)
Với a = 3 ta được pt đường thẳng (d): y = 3x + b
Vì đường thẳng (d) đi qua điểm A(3;7) nên thay x = 3; y = 7 ta được:
7 = 3.3 + b
\(\Leftrightarrow\) b = -2 (TM)
Vậy phương trình đường thẳng (d) là: y = 3x - 2
Chúc bn học tốt!
Đúng 0
Bình luận (0)
a) Giải hệ phương trình
2x+2y=7
2x-2y=3
b) Cho hàm số y = x2 có đồ thị là parabol (p). Vẽ parabol (p) trên mặt phẳng tọa độ Oxy.
a: =>4x=10 và x-y=3/2
=>x=5/2 và y=1
b: 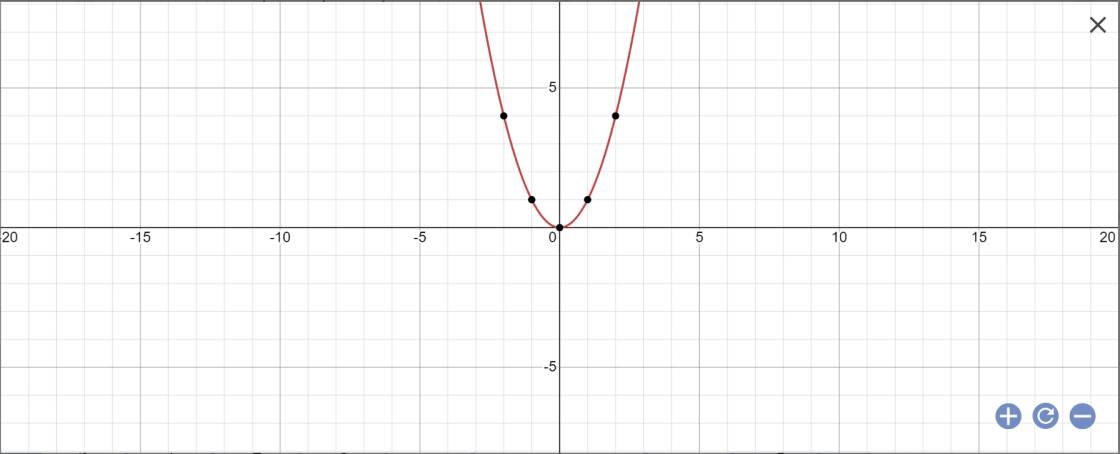
Đúng 0
Bình luận (0)
a) Giải hệ phương trình
2x+2y=7
2x-2y=3
b) Cho hàm số y = x2 có đồ thị là parabol (p). Vẽ parabol (p) trên mặt phẳng tọa độ Oxy.
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y2x2�2�2 và đường thẳng (d) có phương trình y2(m−1)x−m+�2(�−1)�−�+ 1, trong đó m là tham số. a, Vẽ parabol (P).b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y2x2�2�2 và đường thẳng (d) có phương trình y2(m−1)x−m+�2(�−1)�−�+ 1, trong đó m là tham số. a, Vẽ parabol (P).b, Xác đị...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình và đường thẳng (d) có phương trình
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình
và đường thẳng (d) có phương trình
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định
a:
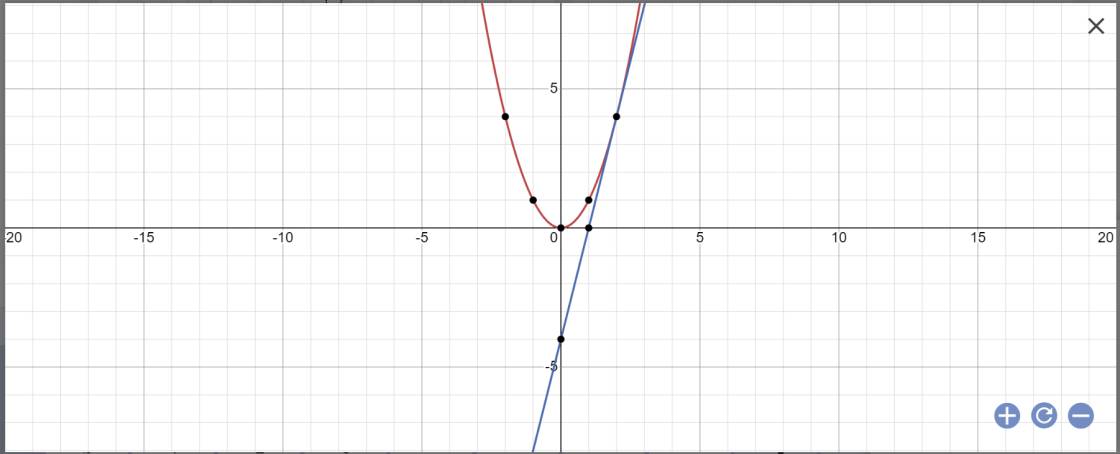
b: PTHĐGĐ là:
2x^2-(2m-2)x+m-1=0
Δ=(2m-2)^2-4*2*(m-1)
=4m^2-8m+4-8m+8
=4m^2-16m+12
=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)
Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0
=>m>3 hoặc m<1
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy. Cho parabol (P) có phương trình y=x2 và đường thẳng (d) có phương trình y=5x -m + 2 ( m là tham số )
1) Điểm A=(2;4) có thuộc đô thị hàm số (P) không. Tại sao
2) Tìm m để dường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có tung độ y1,y2 tỏa mãn y1 + y2 + y1 x y2
1: f(2)=2^2=4
=>A thuộc (P)
2: bạn bổ sung lại đề đi bạn
Đúng 0
Bình luận (1)
Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình
y
1
2
x
2
và hai điểm A, B thuộc (P) có hoành độ lần lượt là
x
A
−
1
;
x
B
2
.a) Tìm tọa độ của hai điểm A, B.b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.c) Tính khoảng cách từ O (gốc tọa độ) đến đường thẳng (d).
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình y = 1 2 x 2 và hai điểm A, B thuộc (P) có hoành độ lần lượt là x A = − 1 ; x B = 2 .
a) Tìm tọa độ của hai điểm A, B.
b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.
c) Tính khoảng cách từ O (gốc tọa độ) đến đường thẳng (d).
a) Vì A, B thuộc (P) nên:
x A = − 1 ⇒ y A = 1 2 ⋅ - 1 2 = 1 2 x B = 2 ⇒ y B = 1 2 ⋅ 2 2 = 2 ⇒ A − 1 ; 1 2 , B ( 2 ; 2 )
b) Gọi phương trình đường thẳng (d) là y = ax + b.
Ta có hệ phương trình:
− a + b = 1 2 2 a + b = 2 ⇔ 3 a = 3 2 2 a + b = 2 ⇔ a = 1 2 b = 1
Vậy (d): y = 1 2 x + 1 .
c) (d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)
=> OC = 1 và OD = 2
Gọi h là khoảng cách từ O tới (d).
Áp dụng hệ thức về cạnh và đường cao vào ∆ vuông OCD, ta có:
1 h 2 = 1 O C 2 + 1 O D 2 = 1 1 2 + 1 2 2 = 5 4 ⇒ h = 2 5 5
Vậy khoảng cách từ gốc O tới (d) là 2 5 5 .
Đúng 0
Bình luận (0)
1. Giải phương trình x (x - 1) (x2 - x + 1) = 6.
2. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y=x2 và đường thẳng d: y = 2x - m +1
Gọi E và F là 2 diểm thuộc (P) có hoành độ lần lượt là -1 và 3. Xác định tọa độ E và F và viết phương trình đường thẳng đi qua 2 điểm E và F.
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y = x ^ 2 và đường thẳng (d) có phương trình (d) v = 2x + m ^ 2 - 2m (với m là tham số)
Xác định tất cả các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ lần lượt là x1, và x2, thỏa mãn điều kiện x1 ^ 2 + 2x2 = 3m
PTHHĐGĐ là:
x^2-2x-m^2+2m=0
Δ=(-2)^2-4(-m^2+2m)
=4+4m^2+8m=(2m+2)^2
Để phương trình có hai nghiệm phân biệt thì 2m+2<>0
=>m<>-1
x1^2+2x2=3m
=>x1^2+x2(x1+x2)=3m
=>x1^2+x2^2+x1x2=3m
=>(x1+x2)^2-x1x2=3m
=>2^2-(-m^2+2m)=3m
=>4+m^2-2m-3m=0
=>m^2-5m+4=0
=>m=1 hoặc m=4
Đúng 0
Bình luận (1)
Trong mặt phẳng tọa độ Oxy, cho Parabol P : y = 2 x 2 . Vẽ đồ thị parabol (P).
a) Vẽ Parabol P : y = 2 x 2
Bảng giá trị giữa x và y:
x |
-2 |
-1 |
0 |
1 |
2 |
y |
8 |
2 |
0 |
2 |
8 |
Vẽ đúng đồ thị
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho Parabol (P): y=2x2. Tính tất cả các điểm thuộc Parabol (P) (khác gốc tọa độ O) có tung độ gấp 2 lần hoành độ