Một cung có số đo ( độ ) là 120° thì cung đó có số đo ( theo đơn vị rađian ) là
VC
Những câu hỏi liên quan
Tìm số đo của các góc lượng giác (OA, OE) và (OA, OP) trên hình 46 (điểm E là điểm chính giữa của cung(A'B'), sđ cung AP = 1/3 sđ cung AB). Viết số đo này theo đơn vị radian và theo đơn vị độ.
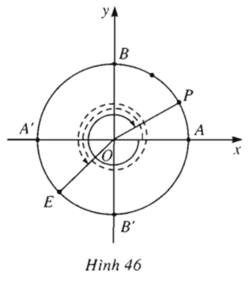
(OA, OE) = sđ cung(AE)= sđ cung(AB') + sđ cung(B'E) = - 90o + (-45)o = -135o = -3/4π (rad)
(OA, OP) = sđ cung(AP)= 1/3 sđ cung(AB) = 1/3 . 90° = 30o = π/6 rad.
Đúng 0
Bình luận (0)
Số đo tính theo đơn vị rađian của góc 135 ° là:
A. 2 π 3
B. 3 π 4
C. 5 π 6
D. 6 π 7
Đáp án: B
Số đo tính theo đơn vị rađian của góc 135 ° là:
Đúng 0
Bình luận (0)
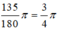
Mỗi khẳng định sau đây đúng hay sai? Vì sao?
a) Hai cung bằng nhau thì số đo bằng nhau.
b) Hai cung có số đo bằng nhau thì bằng nhau.
c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn.
d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.
a) Đúng. Dựa vào cách so sánh hai cung (SGK trang 68).
Chú ý: Khi ta nói hai cung bằng nhau, nghĩa là hai cung này so sánh được (tức chúng cùng nằm trong một đường tròn hoặc trong hai đường tròn bằng nhau). Do đó, theo cách so sánh hai cung đã biết thì hai cung bằng nhau thì số đo bằng nhau.
b) Sai. Nếu hai cung này nằm trong hai đường tròn có bán kính khác nhau thì ta không thể so sánh hai cung.
c) Sai. (Lí luận như câu b)
d) Đúng. (Lí luận như câu a)
Đúng 0
Bình luận (0)
Mỗi khẳng định sau đây đúng hay sai? Vì sao?
a) Hai cung bằng nhau thì có số đo bằng nhau.
b) Hai cung có số đo bằng nhau thì bằng nhau.
c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn hơn.
d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.
a) Đúng
b) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.
c) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.
Đúng 0
Bình luận (1)
1. AB là một cung của (O;R) với sđ cung AB nhỏ là 80 độ. khi đó , góc AOB có số đo là?
2. cho đường tròn (O;R) và dây AB=R. trên cung AB lớn lấy điểm M. số đo cung AMB là?
3. số đo góc tạo bởi tia tiếp tuyến và dây cung bằng?
4. hình tròn ngoại tiếp lục giác đều cạnh 5 cm có diện tích là?
trắc nghiệm thôi..nên giải giúp tôi với ạ^^
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB cung C B có số đo bằng 45 độ M là một điểm nằm trên cung nhỏ AC Gọi N P là các điểm đối xứng với M theo thứ tự qua đường thẳng AB 0C số đo cung nhỏ NP là
Trong một đường tròn, góc ở tâm chắn cung 120 có số đo là *
A.60
B.90
C.30
D.120
Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho số đo cung AB = 60o; số đo cung BC = 90o và số đo cung CD = 120o.
a) Tứ giác ABCD là hình gì?
b) Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.
c) Tính độ dài các cạnh của tứ giác ABCD theo R.
ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3
Đúng 0
Bình luận (0)
Hướng dẫn giải:
ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3
Đúng 0
Bình luận (0)
Trong một đường tròn, góc ở tâm chắn cung 120 có số đo là *
5 điểm
60
90
30
120
Góc ở tâm chắn cung có số đo là: 120o
Đúng 0
Bình luận (0)