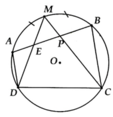
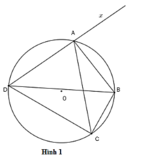
Cho tứ giác ABCD nội tiếp (O;R) sao cho tia BA và CD cắt nhau tại I, tia DA và CB cắt nhau tại K (I,K) nằm ngoài (O) .Phân giác của góc BIC cắt AD,BC lần lượt tại Q,N. Phân giác của góc AKB cắt AB, CD lần lượt tại M,P
a) Chứng minh tứ giác MNPQ là hình thoi
b) Gọi giao điểm 2 đường chéo của MNPQ là G. Chứng minh tam giác IGC đồng dạng tam giác IDG và IK2 = ID.IC + KB.KC
c) Gọi F là trung điểm AB, J là hình chiếu của F trên OB. L là trung điểm của FJ chứng minh AL vuông góc OL