1. Giải phương trình:
(x^2+1)^2+3x(x^2+1)+2x^2=0
2. Tính a+b/a-b biết 2a^2+2b^2=5ab và b>a>0
Giải phương trình: (x^2+1)^2+3x(x^2+1)+2x^2=0
Tính a-b/a+b biết 2a^2+2b^2=5ab và b>a>0
a: \(\Leftrightarrow\left(x^2+1\right)^2+x\left(x^2+x\right)+2x\left(x^2+1\right)+2x^2=0\)
\(\Leftrightarrow\left(x^2+x+1\right)\left(x^2+2x+1\right)=0\)
\(\Leftrightarrow\left(x^2+2x+1\right)=0\)
=>x=-1
b: \(\Leftrightarrow2a^2-5ab+2b^2=0\)
\(\Leftrightarrow2a^2-4ab-ab+2b^2=0\)
\(\Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\)
b>a nên 2b>a
=>2b-a>0
=>2a-b=0
=>b=2a
\(\dfrac{a-b}{a+b}=\dfrac{a-2a}{a+2a}=\dfrac{-1}{3}\)
1. Giải phương trình $\sqrt2.\sqrt{2x^2 + x + 1} - \sqrt{4x-1} + 2x^2+3x-3 = 0$.
2. Cho các số thực dương $a, b, c$ thỏa mãn $ab+bc+ca = 3.$ Chứng minh
$\dfrac{a^3}{b+2c} + \dfrac{b^3}{c+2a} + \dfrac{c^3}{a+2b} \ge 1.$
b, \(\frac{a^3}{b+2c}+\frac{b^3}{c+2a}+\frac{c^3}{a+2b}\ge1\)
\(\frac{a^4}{ab+2ac}+\frac{b^4}{bc+2ab}+\frac{c^4}{ac+2bc}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac+2ac+2ab+2bc}\)( Bunhia dạng phân thức )
mà \(a^2+b^2+c^2\ge ab+bc+ac\)
\(=\frac{\left(ab+bc+ac\right)^2}{3+2\left(ab+ac+bc\right)}=\frac{9}{3+6}=1\)( đpcm )
1.
Điều kiện .
Phương trình tương đương với \\
Với ta có:
.
Suy ra
1.
√2 × √(2x2+x+1) + √(4x-1) + 3x-3=0
⇌[√(4x2+2x+2)-2] - [√(4x-1) -1] + (2x2+3x-2)=0
⇌(4x2+2x-2)/[√(4x2+2x+2)+2] - (4x-2)/[√(4x-1)+1] + (2x-1)(x+2) =0
⇔(2x-1) × [(2x+2)/√(4x2+2x+2+2) - 2/(√4x-1)+1+x+2]=0
Với x≥1/4 thì (2x+2)/(√4x2+2x+2+2)≥0 hoặc x+2>2 hoặc (√4x-1)+1≥1 ⇌ 2/[(√4x-1)+1]≤2
⇒(2x+2)/[(√4x2+2x+2)+2] - 2/[(x-1)+1]+x+2>0-2+2=0
⇌ 2x-1=0⇒x=1/2
Vậy x=1/2
2.
Áp dụng bất đẳng thức ta có :
Vế trái = a4/(ab +2ac) + b4/(bc+2ab) + c4/(ac+2bc)≥[(a2 + b2 +c2)2]/[3(ab+bc+ca) =[(a2+b2+c2)2]/9
Ấp dụng bất đẳng thức ta có :
ab+bc+ca≤a2+b2+c2
Vế trái ≥ [(a2+b2+c2)]/9≥32/9 =1
⇒ Vế trái ≥1 (đpcm)
Dấu = xảy ra khi a=b=c=1
\(A=\left(\dfrac{1}{2a-b}-\dfrac{a^2-1}{2a^3-b+2a-a^2b}\right)\div\left(\dfrac{4a+2b}{a^3b+ab}-\dfrac{2}{a}\right)\)
a) rút gọn biểu thức A
b)tính giá trị biểu thức A biết 4a^2+b^2=5ab a>b>0
Câu 1 : Giải Phương trình
8(x+1/x)+4(x^2+1/x^2)^2-4(x^2+1/x^2)^2(x+1/x)^2=(x+4)^2
Câu 2 :Tìm giá trị nguyên của x để biểu thức B=4x^3-6x^2+8x/2x-1 nhận giá trị nguyên
Câu 3: Cho 1/a+1/b+1/c=0 vs a,b,c khác 0 và m= b^2c^2/a+c^2a^2/b+a^2b^2/a . c/m M=3abc
1. Giải phương trình nghiệm nguyên: y3 = x3 + x2 + x + 1
2. Tìm giá trị lớn nhất của biểu thức: P = \(\frac{x}{\left(x+a\right)^2}\) trong đó a > 0 cho trước
3. Cho 2a2 + 2b2 = 5ab và b>a>0. Tính giá trị biểu thức \(\frac{a+b}{a-b}\)
4. Cho \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\). Tính A = \(\frac{yz}{x^2}+\frac{xz}{y^2}+\frac{xy}{z^2}\)
Tìm a và b để bất phương trình: (x - 2a + b - 1)(x + a - 2b + 1) ≤ 0 có tập nghiệm là đoạn [0; 2]
Tập nghiệm của bất phương trình đã cho là đoạn [2a - b + 1; -a + 2b - 1] (nếu 2a - 6 + 1 ≤ -a + 26 - 1) hoặc là đoạn [-a + 26 - 1 ; 2a - 6 + 1] (nếu -a + 2b - 1 ≤ 2a - 6 - 1)
Do đó để tập nghiệm của bất phương trình đã cho là đoạn [0;2], điều kiện cần và đủ là:
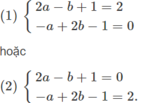
Giải (1) ta được a = b = 1. Giải hệ (2) ta được a = 1/3, b = 5/3
Đáp số: a = b = 1 hoặc a = 1/3, b = 5/3
1/Giải phương trình sau :
\(x-a^2x-\frac{b^2}{b^2-x^2}+a=\frac{x^2}{x^2-b^2}\)
2/ Cho a, b, c là các số khác 0 và đôi một khác nhau , thỏa mãn đẳng thức a + b + c = 0 . Chứng minh rằng :
\(a^3+b^3+c^3+a^2b+ab^2+b^2c+bc^2+c^2a+ca^2=0\)
2, (trích đề thi học sinh giỏi Bến Tre-1993)
\(a^3+a^2b+ca^2+b^3+ab^2+b^2c+c^3+c^2b+c^2a=a^2\left(a+b+c\right)+b^2\left(a+b+c\right)+c^2\left(a+b+c\right)=\left(a+b+c\right)\left(a^2+b^2+c^2\right)\)
mà a+b+c=0 => (a+b+c)(a2+b2+c2)=0
=> đpcm
*bài này tui làm tắt, không hiểu ib
Vừa lm xog bị troll chứ, tuk quá
\(x-a^2x-\frac{b^2}{b^2-x^2}+a=\frac{x^2}{x^2-b^2}\)
\(\Leftrightarrow\frac{x\left(b^2-x^2\right)\left(x^2-b^2\right)}{\left(b^2-x^2\right)\left(x^2-b^2\right)}-\frac{a^2x\left(b^2-x^2\right)\left(x^2-b^2\right)}{\left(b^2-x^2\right)\left(x^2-b^2\right)}-\frac{b^2\left(x^2-b^2\right)}{\left(b^2-x^2\right)\left(x^2-b^2\right)}+\frac{a\left(b^2-x^2\right)\left(x^2-b^2\right)}{\left(b^2-x^2\right)\left(x^2-b^2\right)}=\frac{x^2\left(b^2-x^2\right)}{\left(b^2-x^2\right)\left(x^2-b^2\right)}\)
Khử mẫu :
\(\Leftrightarrow2x^3b^2-xb^4-x^5-2a^2x^3b^2+a^2xb^4+a^2x^5-b^2x^2+b^4+2ab^2x^2-ab^4-ax^4=x^2b^2-x^4\)
Tự xử nốt, lm bài này muốn phát điên mất.
đk \(x\ne\pm b\)
quy đồng mẫu, khử mẫu chung, ta đưa phương trình đã cho về phương trình
\(\left(x^2-b^2\right)\left[\left(1-a\right)-\left(1-a^2\right)x\right]=0\)(1)
với điều kiện x2-b2 khác 0, phương trình (1)trở thành (1-a)-(1-a2)x=0 <=> (1-a2)x=1-a (2)
với a=\(\pm\)1 => (2) vô ngiệm => (1) cũng vô nghiệm và phương trình đã cho cũng vô nghiệm
với a khác \(\pm\)1 => (2) có nghiệm \(x=\frac{1}{1+a}\)
để giá trị x=\(\frac{1}{1+a}\)là nghiệm của phương trình đã cho thì \(\frac{1}{1+a}\ne\pm b\)
kết quả: a=\(\pm1\Rightarrow S=\varnothing\)
\(\hept{\begin{cases}a\ne\pm1\\\frac{1}{1+a}\ne\pm b\end{cases}\Rightarrow S=\left\{\frac{1}{1+a}\right\}}\)
Giải các phương trình sau : 2 4x – 2 a) 2x - 3 = 5 b) (x + 2)(3x - 15) 0 z +1 I - 2 (x+ 1) (2 – 2) Câu 2: (2 điểm) số a) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục 2x + 2 <2+ 3 b) Tìm x để giá trị của biểu thức 3x - 4 nhỏ hơn giá trị của biểu thức 5x - 6
1:
a: 2x-3=5
=>2x=8
=>x=4
b: (x+2)(3x-15)=0
=>(x-5)(x+2)=0
=>x=5 hoặc x=-2
2:
b: 3x-4<5x-6
=>-2x<-2
=>x>1
1 : Giá trị x = -1 là nghiệm của phương trình nào trong các phương trình sau: A. 4x+1 = 3x-2 B. x + 1 = 2x - 3 C. 2x+ 1 = 2 + x D. x + 2 =1
Câu 2 : Trong các phương trình sau, phương trình bậc nhất 1 ẩn là A. x 2 + 2x + 1 = 0 B. -3x + 2 = 0 C. x + y = 0 D. 0x + 1 = 0
Câu 3 : Phương trình (3-x)(2x-5) = 0 có tập nghiệm là : A. S = {- 3; 2,5} ; B. S = {- 3; - 2,5} ; C. S = { 3; 2,5} ; D. S = { 3; - 2,5} .
Câu 4 : Điều kiện xác định của phương trình 1 0 2 1 3 x x x x là A. x 1 2 hoặc x -3 B. x 1 2 C. x -3 D. x 1 2 và x -3
Câu 5 : Với giá trị nào của m thì PT 2mx –m +3 =0 có nghiệm x=2 ? A. m = -1. B. m= -2. C. m= 1. D. m= 2.
Câu 6 : Phương trình tương đương với phương trình x – 3 = 0 là A. x + 2 = -1 B. (x2+ 1)( x- 3) = 0 C. x -1 = -2 D. x = -3
Câu 7 : Nếu a < b thì: A. a + 2018 > b + 2018. B. a + 2018 = b + 2018. C. a + 2018 < b + 2018. D. a + 2018 b + 2018
Câu 8: Nhân cả hai vế của bất đẳng thức a ≤ b với 2 ta được A. -2a ≥ -2b B.2a ≥ 2b C. 2a ≤ 2b D. 2a <2b.
Câu 9: Nhân cả hai vế của một bất đẳng thức với cùng 1 số âm ta được bất đẳng thức A. ngược chiều với bất đẳng thức đã cho. B. lớn hơn bất đẳng thức đã cho. C. cùng chiều với bất đẳng thức đã cho. D. bằng với bất đẳng thức đã cho.
Câu 10: Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào ? A. x<3 B. x<3 C. x > 3 D. x > 3
Câu 11: Hình biểu diễn tập nghiệm của bất phương trình x < 2 là: A. B. C. D.
Câu 12: Tổng tất cả các nghiệm của phương trình 2 5 3 x x
Câu 1: B
Câu 2; A
Câu 3; C
Câu 4: B
Câu 5: A
Câu 6: D
Câu 7: A
Câu 8: C
Câu 9: B
Câu 10: A