Bài 1: Cho tam giác ABC vs đường cao BH,CK
a. C/m tam giác ABH # tam giác ACK b. Cho \(\widehat{ACB}=40\)o . Tính \(\widehat{AKH}\)
Cho tam giác ABC cân tại A, hai đường cao BH và CK ( ).
a) Chứng minh ∆ ABH=∆ACK
b) Chứng minh tam giác AKH là tam giác cân
c) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .
d) Chứng minh: .HK//BC
Cho tam giác ABC nhọn (AB=AC) vẽ đường cao BH , CK của tam giác (H thuộc AC, K thuộc AB )gọi E là giao điểm của BH, Ck a, chứng minh tam giác AHB đồng dạng vs tam giác AkC b, c/m kH song song vs BC
Cho tam giác ABC vuông tại A có đường cao AH
a/ Chứng minh tam giác ABH đồng dạng tam giác CBA.
b/ Gọi M là trung điểm của BH. Kẻ CK vuông góc với AM tại K , CK cắt AH tại I. Chứng minh IA = IH
a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
=>ΔABH đồng dạng với ΔCBA
b: Xét ΔCAM có
CK,AH là đường cao
CK cắt AH tại I
=>I là trực tâm
=>MI vuông góc AC
=>MI//AB
Xét ΔHAB có
M là trung điểm của HB
MI//AB
=>I là trung điểm của AH
=>IA=IH
Cho tam giác ABC cân tại A có đường cao BH và CK cắt nhau tại E a) Chứng minh tam giác ABH = tam giác ACK b) Chứng minh EB = EC c) Chứng minh AE vuông góc BC - Ai giúp mik với ạ , mik cần gấp bài này ( giải chi tiết + có hình vẽ )
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: góc ABH+góc EBC=góc ABC
góc ACK+góc ECB=góc ACB
mà góc ABH=góc ACK;góc ABC=góc ACB
nên góc EBC=góc ECB
=>ΔEBC cân tại E
c: AB=AC
EB=EC
=>AE là trung trực của BC
=>AE vuông góc với BC
Cho tam giác ABC và các đường cao BH, CK. Chứng minh Δ ABH ∼ Δ ACK.
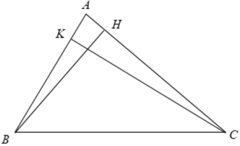
Xét Δ ABH và Δ ACK có
⇒ Δ ABH ∼ Δ ACK ( g - g )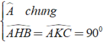
Cho tam giác ABC và các đường cao BH, CK. Chứng minh Δ ABH ∼ Δ ACK.
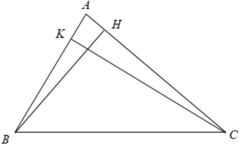
Xét Δ ABH và Δ ACK có
⇒ Δ ABH ∼ Δ ACK ( g - g )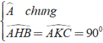
Cho tam giác ABC cân tại A (A<90’) BC,CK là hai đường cao
a)chứng minh :tam giác ABH=tam giác ACK
b)chứng minh:AH=CK
c)gọi I là giao điểm của BH là CK.Chứng minh:Al là tia phân giác của góc A
d)chứng minh:tam giác BIC cân tại I
e)chứng minh:Al vuông góc BC
f)chứng minh Ai là đưuong trung trực của đoạn thẳng BC
g)chứng minh: IH=IK
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
b: ΔAHB=ΔAKC
=>AH=AK
c: Xét ΔAKI vuông tại Kvà ΔAHI vuông tại H có
AI chung
AK=AH
=>ΔAKI=ΔAHI
=>góc KAI=góc HAI
=>AI là phân giác của góc BAC
d: Xét ΔIBC có góc IBC=góc ICB
nên ΔICB cân tại I
e: ΔABC cân tại A
mà AI là phân giác
nên AI vuông góc BC
f: ΔABC cân tại A
ma AI là đường cao
nên AI là trung trực của BC
g: ΔAKI=ΔAHI
=>KI=HI
Cho tam giác ABC vuông tại A có đường cao AH, AB=6 cm ,AC=8cm
a)CM tam giác ABH đồng dạng vs Tam giác ABC . CM tam giác AHC đồng dạng vs Tam giác ABC
b)CM tam giác AHB đồg dạng vs tam giác AHC
c) Tính BH
Cho tam giác ABC vuông cân tại A có AB = 5 cm. Qua A kẻ đường thẳng d sao cho B và C thuộc cùng 1 nửa mặt phẳng bờ d . Vẽ BH, CK vuông góc với d ( H, K thuộc d )
a) C/m: tam giác ABH = tam giác BAK
b) Tính BH bình phương + CK bình Phương
cho tam giác abc và các đường cao BH,CK
a) chứng minh tam giác ABH đồng dạng với tam giác ACK
b)Cho góc ACB= 40, Tính góc AKH