giải phương trình:
\(x^4+x^3-4x^2+x+1=0\)
Bài 1: Giải phương trình và bất phương trình sau: 1. 5.(2-3x). (x-2) = 3.( 1-3x) 2. 4x^2 + 4x + 1= 0 3. 4x^2 - 9= 0 4. 5x^2 - 10=0 5. x^2 - 3x= -2 6. |x-5| - 3= 0
1. Giải phương trình: \(\sqrt{x-2}+\sqrt{4-x}=\sqrt{2}\) .
2. Giải phương trình: \(4x^4-7x^3+9x^2-10x+4=0\).
3. Giải hệ phương trình: \(\left\{{}\begin{matrix}x^2+y^2=3-xy\\x^4+y^4=2\end{matrix}\right.\) .
Bài 1: ĐKXĐ: $2\leq x\leq 4$
PT $\Leftrightarrow (\sqrt{x-2}+\sqrt{4-x})^2=2$
$\Leftrightarrow 2+2\sqrt{(x-2)(4-x)}=2$
$\Leftrightarrow (x-2)(4-x)=0$
$\Leftrightarrow x-2=0$ hoặc $4-x=0$
$\Leftrightarrow x=2$ hoặc $x=4$ (tm)
Bài 2:
PT $\Leftrightarrow 4x^3(x-1)-3x^2(x-1)+6x(x-1)-4(x-1)=0$
$\Leftrightarrow (x-1)(4x^3-3x^2+6x-4)=0$
$\Leftrightarrow x=1$ hoặc $4x^3-3x^2+6x-4=0$
Với $4x^3-3x^2+6x-4=0(*)$
Đặt $x=t+\frac{1}{4}$ thì pt $(*)$ trở thành:
$4t^3+\frac{21}{4}t-\frac{21}{8}=0$
Đặt $t=m-\frac{7}{16m}$ thì pt trở thành:
$4m^3-\frac{343}{1024m^3}-\frac{21}{8}=0$
$\Leftrightarrow 4096m^6-2688m^3-343=0$
Coi đây là pt bậc 2 ẩn $m^3$ và giải ta thu được \(m=\frac{\sqrt[3]{49}}{4}\) hoặc \(m=\frac{-\sqrt[3]{7}}{4}\)
Khi đó ta thu được \(x=\frac{1}{4}(1-\sqrt[3]{7}+\sqrt[3]{49})\)
Nãy mình tìm được một cách giải tương tự cho câu 2.
PT \(\Leftrightarrow\left(x-1\right)\left(4x^3-3x^2+6x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x^3-3x^2+6x-4=0\left(1\right)\end{matrix}\right.\)
Vậy pt có 1 nghiệm bằng 1.
\(\left(1\right)\Rightarrow8x^3-6x^2+12x-8=0\)
\(\Leftrightarrow7x^3+x^3-6x^2+12x-8=0\)
\(\Leftrightarrow\left(x-2\right)^3=-7x^3\)
\(\Leftrightarrow x-2=-\sqrt[3]{7}x\)
\(\Leftrightarrow x=\dfrac{2}{1+\sqrt[3]{7}}\)
Vậy pt có nghiệm \(S=\left\{1;\dfrac{2}{1+\sqrt[3]{7}}\right\}\)
Lưu ý: Nghiệm của người kia hoàn toàn tương đồng với nghiệm của mình (\(\dfrac{2}{1+\sqrt[3]{7}}=\dfrac{1}{4}\left(1-\sqrt[3]{7}+\sqrt[3]{49}\right)\))
1) Giải các phương trình sau : a) x-3/x=2-x-3/x+3 b) 3x^2-2x-16=0 2) Giải bất phương trình sau: 4x-3/4>3x-5/3-2x-7/12
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
Giải phương trình:
1. \(x^4-6x^2-12x-8=0\)
2. \(\dfrac{x}{2x^2+4x+1}+\dfrac{x}{2x^2-4x+1}=\dfrac{3}{5}\)
3. \(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)
4. \(2x^2.\sqrt{-4x^4+4x^2+3}=4x^4+1\)
5. \(x^2+4x+3=\sqrt{\dfrac{x}{8}+\dfrac{1}{2}}\)
6. \(\left\{{}\begin{matrix}4x^3+xy^2=3x-y\\4xy+y^2=2\end{matrix}\right.\)
7. \(\left\{{}\begin{matrix}\sqrt{x^2-3y}\left(2x+y+1\right)+2x+y-5=0\\5x^2+y^2+4xy-3y-5=0\end{matrix}\right.\)
8. \(\left\{{}\begin{matrix}\sqrt{2x^2+2}+\left(x^2+1\right)^2+2y-10=0\\\left(x^2+1\right)^2+x^2y\left(y-4\right)=0\end{matrix}\right.\)
1.
\(x^4-6x^2-12x-8=0\)
\(\Leftrightarrow x^4-2x^2+1-4x^2-12x-9=0\)
\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=2x+3\\x^2-1=-2x-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\\x^2+2x+2=0\end{matrix}\right.\)
\(\Leftrightarrow x=1\pm\sqrt{5}\)
3.
ĐK: \(x\ge-9\)
\(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)
\(\Leftrightarrow\left(x^2-x+1\right)\left(\sqrt{x+9}+x^2-9\right)=0\)
\(\Leftrightarrow\sqrt{x+9}+x^2-9=0\left(1\right)\)
Đặt \(\sqrt{x+9}=t\left(t\ge0\right)\Rightarrow9=t^2-x\)
\(\left(1\right)\Leftrightarrow t+x^2+x-t^2=0\)
\(\Leftrightarrow\left(x+t\right)\left(x-t+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-t\\x=t-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{x+9}\\x=\sqrt{x+9}-1\end{matrix}\right.\)
\(\Leftrightarrow...\)
2.
ĐK: \(x\ne\dfrac{2\pm\sqrt{2}}{2};x\ne\dfrac{-2\pm\sqrt{2}}{2}\)
\(\dfrac{x}{2x^2+4x+1}+\dfrac{x}{2x^2-4x+1}=\dfrac{3}{5}\)
\(\Leftrightarrow\dfrac{1}{2x+\dfrac{1}{x}+4}+\dfrac{1}{2x+\dfrac{1}{x}-4}=\dfrac{3}{5}\)
Đặt \(2x+\dfrac{1}{x}+4=a;2x+\dfrac{1}{x}-4=b\left(a,b\ne0\right)\)
\(pt\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{5}\left(1\right)\)
Lại có \(a-b=8\Rightarrow a=b+8\), khi đó:
\(\left(1\right)\Leftrightarrow\dfrac{1}{b+8}+\dfrac{1}{b}=\dfrac{3}{5}\)
\(\Leftrightarrow\dfrac{2b+8}{\left(b+8\right)b}=\dfrac{3}{5}\)
\(\Leftrightarrow10b+40=3\left(b+8\right)b\)
\(\Leftrightarrow\left[{}\begin{matrix}b=2\\b=-\dfrac{20}{3}\end{matrix}\right.\)
TH1: \(b=2\Leftrightarrow...\)
TH2: \(b=-\dfrac{20}{3}\Leftrightarrow...\)
1.Giải phương trình:
\(\sqrt{x^2-4}-x^2+4=0\)
2.Giải phương trình:
\(\sqrt{x^2-4x+5}+\sqrt{x^2-4x+8}+\sqrt{x^2-4x+9}=3+\sqrt{5}\)
1. \(\sqrt{x^2-4}-x^2+4=0\)( ĐK: \(\orbr{\begin{cases}x\ge2\\x\le-2\end{cases}}\))
\(\Leftrightarrow\sqrt{x^2-4}=x^2-4\)
\(\Leftrightarrow\left(x^2-4\right)^2=x^2-4\)
\(\Leftrightarrow\left(x^2-4\right)^2-\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(x^2-4-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2=4\\x^2=5\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\pm2\left(tm\right)\\x=\pm\sqrt{5}\left(tm\right)\end{cases}}\)
Vậy pt có tập no \(S=\left\{2;-2;\sqrt{5};-\sqrt{5}\right\}\)
2. \(\sqrt{x^2-4x+5}+\sqrt{x^2-4x+8}+\sqrt{x^2-4x+9}=3+\sqrt{5}\)ĐK: \(\hept{\begin{cases}x^2-4x+5\ge0\\x^2-4x+8\ge0\\x^2-4x+9\ge0\end{cases}}\)
\(\Leftrightarrow\sqrt{x^2-4x+5}-1+\sqrt{x^2-4x+8}-2+\sqrt{x^2-4x+9}-\sqrt{5}=0\)
\(\Leftrightarrow\frac{x^2-4x+4}{\sqrt{x^2-4x+5}+1}+\frac{x^2-4x+4}{\sqrt{x^2-4x+8}+2}+\frac{x^2-4x+4}{\sqrt{x^2-4x+9}+\sqrt{5}}=0\)
\(\Leftrightarrow\left(x-2\right)^2\left(\frac{1}{\sqrt{x^2-4x+5}+1}+\frac{1}{\sqrt{x^2-4x+8}+2}+\frac{1}{\sqrt{x^2}-4x+9+\sqrt{5}}\right)=0\)
Từ Đk đề bài \(\Rightarrow\frac{1}{\sqrt{x^2-4x+5}+1}+\frac{1}{\sqrt{x^2-4x+8}+2}+\frac{1}{\sqrt{x^2}-4x+9+\sqrt{5}}>0\)
\(\Rightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy pt có no x=2
Giải các bất phương trình sau:
a) \(2{x^2} + 3x + 1 \ge 0\)
b) \( - 3{x^2} + x + 1 > 0\)
c) \(4{x^2} + 4x + 1 \ge 0\)
d) \( - 16{x^2} + 8x - 1 < 0\)
e) \(2{x^2} + x + 3 < 0\)
g) \( - 3{x^2} + 4x - 5 < 0\)
a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
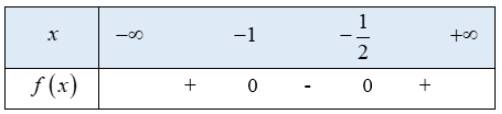
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
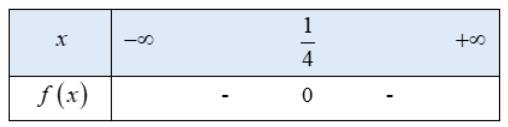
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)
giải phương trình
a)x*4+x*3-4x*2+x+1=0
b)x*4+x*3-10x*2+x+1=0
c)x*4+3x*3-14x*2-6x+4=0
giải các phương trình sau
a)\(\sqrt{x^2-1}\)+1=x2
b)\(\sqrt{x-2}\)+\(\sqrt{x-3}\)= -5
c) \(\sqrt{x^2+4x+4}\)+|x-4|=0
a) ĐKXĐ: \(x^2-1\ge0\)
Đặt \(\sqrt{x^2-1}=t\left(t\ge0\right)\)
\(\Rightarrow t=t^2\Rightarrow t\left(t-1\right)=0\Rightarrow\left[{}\begin{matrix}t=0\\t=1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\sqrt{x^2-1}=0\\\sqrt{x^2-1}=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm1\\x=\pm\sqrt{2}\end{matrix}\right.\)
b) ĐKXĐ: \(x\ge2\)
Ta có: \(\sqrt{x-2}+\sqrt{x-3}\ge0\) mà \(\sqrt{x-2}+\sqrt{x-3}=-5< 0\Rightarrow\) không có x thỏa
c) \(\sqrt{x^2+4x+4}+\left|x-4\right|=0\)
\(\Rightarrow\left|x+2\right|+\left|x-4\right|=0\) mà \(\left|x+2\right|+\left|x-4\right|\ge0\Rightarrow\left\{{}\begin{matrix}x+2=0\\x-4=0\end{matrix}\right.\)
\(\Rightarrow\) không có x thỏa
Bài 1:giải các phương trình sau:
a) (x-3).(x+7)=0 b) (x-2)^2+(x-2).(x-3)=0 c)x^2-5x+6=0
Bài 2:giải các phương trình chứa ẩn ở mẫu sau:
a)x/x+1-1=3/2x b)4x/x-2-7/x=4
Bài 3:giải phương trình sau
a)2x^2-5x-7=0 b)1/x^2-4+2x/x-2=2x/x+2
giúp mình với,mình đang cần gấp
Mình khuyên bạn thế này :
Bạn nên tách những câu hỏi ra
Như vậy các bạn sẽ dễ giúp
Và cũng có nhiều bạn giúp hơn !
Bài 1.
a) ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
Vậy S = { 3 ; -7 }
b) ( x - 2 )2 + ( x - 2 )( x - 3 ) = 0
<=> ( x - 2 )( x - 2 + x - 3 ) = 0
<=> ( x - 2 )( 2x - 5 ) = 0
<=> x - 2 = 0 hoặc 2x - 5 = 0
<=> x = 2 hoặc x = 5/2
Vậy S = { 2 ; 5/2 }
c) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> x - 2 = 0 hoặc x - 3 = 0
<=> x = 2 hoặc x = 3
Bài 2.
a) \(\frac{x}{x+1}-1=\frac{3}{2}x\)
ĐKXĐ : x khác -1
<=> \(\frac{x}{x+1}-\frac{x+1}{x+1}=\frac{3}{2}x\)
<=> \(\frac{-1}{x+1}=\frac{3x}{2}\)
=> 3x( x + 1 ) = -2
<=> 3x2 + 3x + 2 = 0
Vi 3x2 + 3x + 2 = 3( x2 + x + 1/4 ) + 5/4 = 3( x + 1/2 )2 + 5/4 ≥ 5/4 > 0 ∀ x
=> phương trình vô nghiệm
b) \(\frac{4x}{x-2}-\frac{7}{x}=4\)
ĐKXĐ : x khác 0 ; x khác 2
<=> \(\frac{4x^2}{x\left(x-2\right)}-\frac{7x-14}{x\left(x-2\right)}=\frac{4x^2-8x}{x\left(x-2\right)}\)
=> 4x2 - 7x + 14 = 4x2 - 8x
<=> 4x2 - 7x - 4x2 + 8x = -14
<=> x = -14 ( tm )
Vậy phương trình có nghiệm x = -14
giải phương trình
1)\(\sqrt{9\left(x-1\right)}=21\)
2)\(\sqrt{1-x}+\sqrt{4-4x}-\dfrac{1}{3}\sqrt{16-16x}+5=0\)
3)\(\sqrt{2x}-\sqrt{50}=0\)
4)\(\sqrt{4x^2+4x+1}=6\)
5)\(\sqrt{\left(x-3\right)^2}=3-x\)
1) \(\sqrt[]{9\left(x-1\right)}=21\)
\(\Leftrightarrow9\left(x-1\right)=21^2\)
\(\Leftrightarrow9\left(x-1\right)=441\)
\(\Leftrightarrow x-1=49\Leftrightarrow x=50\)
2) \(\sqrt[]{1-x}+\sqrt[]{4-4x}-\dfrac{1}{3}\sqrt[]{16-16x}+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}+\sqrt[]{4\left(1-x\right)}-\dfrac{1}{3}\sqrt[]{16\left(1-x\right)}+5=0\)
\(\)\(\Leftrightarrow\sqrt[]{1-x}+2\sqrt[]{1-x}-\dfrac{4}{3}\sqrt[]{1-x}+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}\left(1+3-\dfrac{4}{3}\right)+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}.\dfrac{8}{3}=-5\)
\(\Leftrightarrow\sqrt[]{1-x}=-\dfrac{15}{8}\)
mà \(\sqrt[]{1-x}\ge0\)
\(\Leftrightarrow pt.vô.nghiệm\)
3) \(\sqrt[]{2x}-\sqrt[]{50}=0\)
\(\Leftrightarrow\sqrt[]{2x}=\sqrt[]{50}\)
\(\Leftrightarrow2x=50\Leftrightarrow x=25\)
1) \(\sqrt{9\left(x-1\right)}=21\) (ĐK: \(x\ge1\))
\(\Leftrightarrow3\sqrt{x-1}=21\)
\(\Leftrightarrow\sqrt{x-1}=7\)
\(\Leftrightarrow x-1=49\)
\(\Leftrightarrow x=49+1\)
\(\Leftrightarrow x=50\left(tm\right)\)
2) \(\sqrt{1-x}+\sqrt{4-4x}-\dfrac{1}{3}\sqrt{16-16x}+5=0\) (ĐK: \(x\le1\))
\(\Leftrightarrow\sqrt{1-x}+2\sqrt{1-x}-\dfrac{4}{3}\sqrt{1-x}+5=0\)
\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}+5=0\)
\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}=-5\) (vô lý)
Phương trình vô nghiệm
3) \(\sqrt{2x}-\sqrt{50}=0\) (ĐK: \(x\ge0\))
\(\Leftrightarrow\sqrt{2x}=\sqrt{50}\)
\(\Leftrightarrow2x=50\)
\(\Leftrightarrow x=\dfrac{50}{2}\)
\(\Leftrightarrow x=25\left(tm\right)\)
4) \(\sqrt{4x^2+4x+1}=6\)
\(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\)
\(\Leftrightarrow\left|2x+1\right|=6\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\left(ĐK:x\ge-\dfrac{1}{2}\right)\\2x+1=-6\left(ĐK:x< -\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=5\\2x=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(tm\right)\\x=-\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)
5) \(\sqrt{\left(x-3\right)^2}=3-x\)
\(\Leftrightarrow\left|x-3\right|=3-x\)
\(\Leftrightarrow x-3=3-x\)
\(\Leftrightarrow x+x=3+3\)
\(\Leftrightarrow x=\dfrac{6}{2}\)
\(\Leftrightarrow x=3\)
1) => 9(x-1)=\(21^2\)
=> 9x-9=441
=> 9x=450
=> x=50
2)=>\(\sqrt{1-x}\) + \(\sqrt{4\left(1-x\right)}\)-\(\dfrac{1}{3}\sqrt{16\left(1-x\right)}\)+5=0
=>\(\sqrt{1-x}\)\(\left(1+2-\dfrac{1}{3}.4\right)\)+5=0
=>\(\dfrac{5}{3}\sqrt{1-x}\) +5=0
=>\(\sqrt{1-x}\)=-3
Phuong trinh vo nghiem