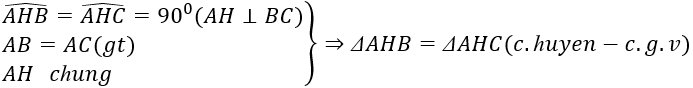cho tam giác ABC vuông tại A kẻ AH vuông góc với BC tại H cm BC+AH>AB+AC
CD
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A ( AB<AC) kẻ AH vuông góc với BC , phân giác góc HAC cắt BC tại D
a) Cm : tam giác ABD cân tại B
b) Từ H kẻ đường thẳng vuông góc với AD cắt Ac tại E . CM: DE vuông góc AC
c) Cho AB=15cm, AH=12cm. Tính AD
Cho tam giác ABC vuông tại A, AB < AC. Kẻ Ah vuông góc với BC, H thuộc BC, D là một điểm thuộc cạnh AC sao cho AD = AB.
a. Kẻ DE, DK vuông góc với BC, AH tại E, K. CM DK = HE.
b. CM góc ABH = góc DAK.
c. CM tam giác AHB bằng tam giác DKA.
d. CM AH = HE.
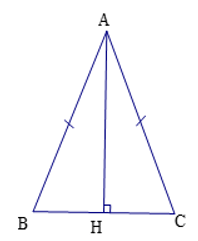
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.1) Chứng minh tam giác ABH tam giác ACH và H là trung điểm của BC.2) Nếu có AB 10cm, BC 12 cm, hãy tính độ dài đoạn thẳng AH.3) Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Lấy các điểm M và N sao cho E là trung điểm của HM, F là trung điểm của HN. Chứng minh AN AH.4) Tam giác ABC cần thêm điều kiện gì thì A là trung điểm của MN?Giúp mik vs ạ mik đang cần gấp.
Đọc tiếp
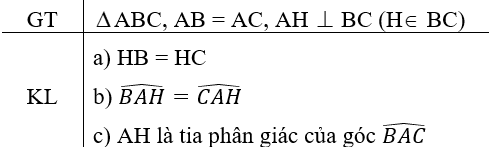
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.
1) Chứng minh tam giác ABH = tam giác ACH và H là trung điểm của BC.
2) Nếu có AB = 10cm, BC = 12 cm, hãy tính độ dài đoạn thẳng AH.
3) Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Lấy các điểm M và N sao cho E là trung điểm của HM, F là trung điểm của HN. Chứng minh AN = AH.
4) Tam giác ABC cần thêm điều kiện gì thì A là trung điểm của MN?
Giúp mik vs ạ mik đang cần gấp.
1: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
2: Ta có: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=10^2-6^2=64\)
=>\(HA=\sqrt{64}=8\left(cm\right)\)
3: Xét ΔAHN có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔAHN cân tại A
=>AH=AH
4: Xét ΔAHM có
AE là đường trung tuyến
AE là đường cao
Do đó: ΔAHM cân tại A
=>AM=AH
Ta có: ΔAHN cân tại A
mà AC là đường cao
nên AC là phân giác của góc HAN
=>\(\widehat{HAN}=2\cdot\widehat{HAC}\)
Ta có: ΔAHM cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAM
=>\(\widehat{HAM}=2\cdot\widehat{HAB}\)
Ta có: AM=AH
AH=AN
Do đó: AM=AN
Ta có: \(\widehat{HAM}+\widehat{HAN}=\widehat{MAN}\)
=>\(\widehat{MAN}=2\cdot\left(\widehat{HAB}+\widehat{HAC}\right)\)
=>\(\widehat{MAN}=2\cdot\widehat{BAC}\)
Để A là trung điểm của MN thì AM=AN và góc MAN=180 độ
=>góc MAN=180 độ
=>\(2\cdot\widehat{BAC}=180^0\)
=>\(\widehat{BAC}=90^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB AC 10 cm ; BC 12cm . Kẻ AH vuông góc BC tại H . a) Chứng minh tam giác ABH tam giác ACH . Từ đó suy ra H là trung điểm của đoạn thẳng BC . b) Tính độ dài đoạn thẳng AH . c) Kẻ HI vuông góc AB tại I ; HK vuông góc AC tại K . Vẽ các điểm D E, sao cho I, K lần lượt là trung điểm của HD HE , . Chứng minh AE AH . d) tam giác ADE là tam giác gì? Vì sao? Chứng minh DE / / BC . e) Tìm điều kiện của tam giác ABC để A là trung điểm của DE .
Đọc tiếp
Cho tam giác ABC có AB = AC =10 cm ; BC =12cm . Kẻ AH vuông góc BC tại H .
a) Chứng minh tam giác ABH = tam giác ACH . Từ đó suy ra H là trung điểm của đoạn thẳng BC .
b) Tính độ dài đoạn thẳng AH .
c) Kẻ HI vuông góc AB tại I ; HK vuông góc AC tại K . Vẽ các điểm D E, sao cho I, K lần lượt là trung điểm của HD HE , . Chứng minh AE = AH .
d) tam giác ADE là tam giác gì? Vì sao? Chứng minh DE / / BC .
e) Tìm điều kiện của tam giác ABC để A là trung điểm của DE .
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
b: BH=CH=6cm
=>AH=8cm
c: Xét ΔAHE có
AK là đường cao
AK là đường trung tuyến
Do đó: ΔAHE cân tại A
hay AE=AH
d: Xét ΔADH có
AI là đường cao
AI là đườngtrung tuyến
Do đó:ΔADH cân tại A
=>AD=AH=AE
=>ΔADE cân tại A
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc BC (H thuộc BC).
a/ Chứng minh Tam giác AHB = Tam giác AHC. Từ đó suy ra HB = HC
b/ Biết AH = 8 cm, BC = 12 cm. Tính độ dài AC.
c/ Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC). Chứng minh Tam giác HDE cân.
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: BH=CH=12/2=6cm
=>AC=căn AH^2+HC^2=10cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc BC (H thuộc BC).
a/ Chứng minh Tam giác AHB = Tam giác AHC. Từ đó suy ra HB = HC
b/ Biết AH = 8 cm, BC = 12 cm. Tính độ dài AC.
c/ Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC). Chứng minh Tam giác HDE cân.
Chứng minh
a) Xét tam giác AHB và tam giác AHC có:
Đúng 1
Bình luận (0)
b) có tam giác ABC cân tại A
=> AB=AC
có BC=BH+HC
=> BC=12:2=6(cm)
=> BH=6;HC=6
có tam giác AHC
=> áp dụng định lí pytago có
=>AH2+HC2=AC2
=>82+62=AC2
=>AC2=102
=>AC=10
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A,(AB<AC), kẻ ah vuông góc với BC, phân giác của góc HAC cắt BC tại D
a, CM tam giác ABD cân taị D
b, Từ H kẻ đường thẳng vuông góc với AD tại E. CM DE vuông góc AC
c, Cho AB=15cm, AH=12cm.Tính AD
Cho tam giác ABC vuông tại A ,AB bằng 9 cm ,AC bằng 12 cm .Kẻ AH vuông góc với BC tại H
a/Chứng minh tam giác abh đồng dạng tam giác ABC và AB mũ 2 = Hb . BC
b/tính BC, ah
c/tia phân giác góc ACB cắt ah tại I và cắt AB tại D Chứng minh CB.CI=CA.CDCD
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
b: BC=căn 9^2+12^2=15cm
AH=9*12/15=7,2cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC = 52 cm, AB = 20 cm, AC = 48 cm.
a. Tam giác ABC có vuông không?
b. Kẻ AH vuông góc với BC tại H. Tính độ dài AH.
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{240}{13}\left(cm\right)\)
Đúng 2
Bình luận (0)
a. Ta có: BC2=AB2+AC2, suy ra tam giác ABC vuông tại A.
b. Ta có: AB.AC=AH.BC, suy ra AH=AB.AC/BC=20.48/52=240/13.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H thuộc BC)
a CM tam giác AHB=tam giác AHC
b từ điểm H kẻ HK vuông góc với AB tại K, HF vuông góc với AC tại F. CM: HK=HF
c CM : KE//BC
`Answer:`
Sửa đề phần c: Chứng minh KF//BC.
a. Xét `\triangleAHB` và `\triangleAHC`
`AH` chung
`\hat{AHB}=\hat{AHC}=90^o`
`AB=AC`
`=>\triangleAHB=\triangleAHC(ch-cgv)`
b. Xét `\triangleFAH` và `\triangleKAH`
`AH` chung
`\hat{FAH}=\hat{KAH}`
`\hat{AFH}=\hat{AKH}=90^o`
`=>\triangleFAH=\triangleKAH(ch-gn)`
`=>HK=HF`
c. Theo phần b. `\triangleFAH=\triangleKAH`
`=>AF=AK`
`=>\triangleAFK` cân ở `A`
Ta có: `\triangleAFK` cân ở `A` và `\triangleABC` cân ở `A`
`=>\hat{AFK}=\hat{ABC}` mà hai góc này ở vị trí đồng vị \(\Rightarrow KF//BC\)
hình tự vẽ nhé.
xét: \(\Delta AHB\) VÀ \(\Delta AHC\) CÓ:
\(\widehat{ABH}=\widehat{ACH}\)(DO TAM GIÁC ABC CÂN TẠI A)
\(AB=AC\)(DO TAM GIÁC ABC CÂN TẠI A)
\(\widehat{AHB}=\widehat{AHC}=90^0\)
\(\Rightarrow\Delta AHB=\Delta AHC\left(ch-gn\right)\left(1\right)\)
b) TỪ (1)\(\Rightarrow BH=CH\)(2 cạnh tương ứng)
XÉT: \(\Delta KBH\)VÀ \(\Delta FCH\) CÓ:
\(BH=CH\left(cmt\right)\)
\(\widehat{BKH}=\widehat{CFH}=90^0\)
\(\widehat{KBH}=\widehat{FCH}\left(\widehat{B}=\widehat{C}\right)\)
\(\Rightarrow\Delta KBH=\Delta FCH\left(ch-gn\right)\)
\(\Rightarrow HK=HF;BK=FC\)(2 cạnh tương ứng)(đpcm)
c) ta có: \(AB=AC;;BK=FK\left(cmt\right)\)
\(\Rightarrow AB-BK=AC-FC\)
\(\Rightarrow AK=AF\Rightarrow\Delta AKF\) cân tại A
\(\Rightarrow\widehat{AKF}=\frac{180^0-\widehat{A}}{2}\left(2\right)\)
lại có \(\Delta ABC\)cân tại A\(\Rightarrow\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\left(3\right)\)
TỪ (2)VÀ (3)\(\Rightarrow\widehat{AKF}=\widehat{ABC}\left(=\frac{180^0-\widehat{A}}{2}\right)\)
mà 2 góc này ở vị trí đồng vị \(\Rightarrow KF\\ BC\left(đpcm\right)\)