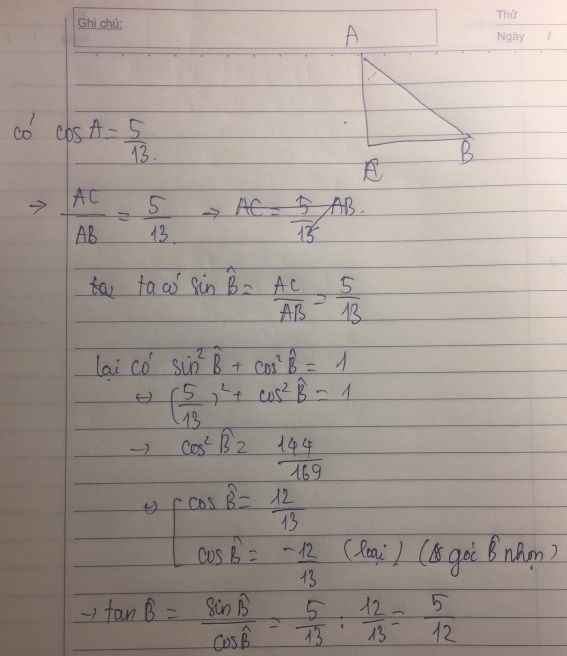cho tam giác ABC có b=7, c=5, cosA=\(\dfrac{3}{5}\).tính đường cao \(h_a\) của tam giác ABC
PN
Những câu hỏi liên quan
Cho tam giác ABC có b 7; c 5, cosA 3/5. Đường cao ha của tam giác ABC là A. B. 6. C. D.
Đọc tiếp
Cho tam giác ABC có b = 7; c = 5, cosA = 3/5. Đường cao ha của tam giác ABC là
A. ![]()
B. 6.
C. ![]()
D. ![]()
Chọn A.
Áp dụng định lí cosin trong tam giác ta có:
a2 = b2 + c2 = 2bc.cosA = 72 + 52 - 2.7.5.3/5 = 32
Nên ![]()
Mặt khác: sin2A + cos2A = 1 nên sin2A = 1 - cos2A = 16/25
Mà sinA > 0 nên sinA = 4/5
Mà: 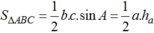
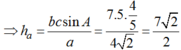
Đúng 1
Bình luận (0)
* Cho tam giác ABC vuông tại C. Biết cosA=\(\dfrac{5}{13}\). Tính tan B
\(\sin\widehat{A}=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
\(\cot\widehat{A}=\dfrac{5}{13}:\dfrac{12}{13}=\dfrac{5}{12}\)
\(\tan\widehat{B}=\dfrac{5}{12}\)
Đúng 2
Bình luận (0)
Cho tam giác vuông ABC vuông tại A có AB=6cm,AC=8cm. Kẻ đường cao AH. a) Chứng minh tam giác ABC đồng dạng với tam giác HBA b) Tính diện tích tam giác hba biết tỉ số đồng dạng của tam giác ABC và HBA là\(\dfrac{5}{3}\)
a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: \(\dfrac{S_{ABC}}{S_{HBA}}=\dfrac{25}{9}\)
nên \(S_{HBA}=24:\dfrac{25}{9}=24\cdot\dfrac{9}{25}=8.64\left(cm^2\right)\)
Đúng 1
Bình luận (1)
Tam giác ABC có \(a=4\sqrt{7}cm;b=6cm;c=8cm\). Tính diện tích S, đường cao \(h_a\) và bán kính R của đường tròn ngoại tiếp tam giác đó ?
Tam giác ABC có cạnh \(a=2\sqrt{3};b=2;\widehat{C}=30^0\)
a) Tính cạnh c, góc A và diện tích S của tam giác ABC
b) Tính chiều cao \(h_a\) và đường trung tuyến \(m_a\) của tam giác ABC
3) Hãy ghi đáp án và lời giải cho câu hỏi sau:
Cho △ABC có \(b=7;c=5;\cos A=\dfrac{3}{5}\). Đường cao \(h_a\) của △ABC là:
\(A.\dfrac{7\sqrt{2}}{2}\)
\(B.8\)
\(C.8\sqrt{3}\)
\(D.80\sqrt{3}\)
Xem thêm câu trả lời
Cho tam giác ABC có AB = 5, AC = 6, BC =7. Tính cosA.
Áp dụng định lí cosin trong tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)\( \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \(AB = c = 5,{\rm{ }}AC = b = 6,{\rm{ }}BC = a = 7\).
\( \Rightarrow \cos A = \frac{{{6^2} + {5^2} - {7^2}}}{{2.5.6}} = \frac{1}{5}\)
Chú ý
Từ định lí cosin, ta suy cách tìm góc khi biết độ dài 3 cạnh
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\;\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\;\cos C = \frac{{{b^2} + {a^2} - {c^2}}}{{2ab}}.\)
Đúng 1
Bình luận (0)
Tam giác ABC có dộ dài 3 đường cao là: \(h_a,h_b,h_c\). Hỏi trong 5 bộ số sao, bộ số nào có thể là độ dài 3 đường cao của tam giác ABC
(A). (6,8,8) ; (B). (1;0,5;1,5) ; (C). (2,4,4) ; (D). (3,6,8) ; (E). (3,6,9)
Giải thích cách làm giùm thanks
Không mất tính tổng quát, giả sử ha là độ dài đường cao ứng với BC. Định nghĩa tương tự với hb và hc
Phương án A: Xét ha = 6, hb = hc = 8. Giả sử tồn tại tam giác ABC nhận bộ (6,8,8) làm độ dài 3 đường cao
Ta có 2.SABC = 6BC = 8AB = 8CA. Suy ra \(BC=\frac{4}{3}AB=\frac{4}{3}CA\)
Đặt BC = a. Khi đó \(AB=CA=\frac{3}{4}a\). Ta thấy:
\(AB+CA=\frac{3}{4}a+\frac{3}{4}a=\frac{3}{2}a>a=BC\)
\(BC+CA=BC+AB=a+\frac{3}{4}a=\frac{7}{4}a>\frac{3}{4}a=AB=CA\) (Đúng với ĐBT tam giác)
=> Tồn tại tam giác ABC nhận bộ (6,8,8) làm độ dài 3 đường cao => Chọn (A).
Phương án B: Loại vì một tam giác không thể chứa 5 đường cao.
Phương án C: Lập luận tương tự ta có \(BC=2CA=2AB\)
Tức là \(CA+AB=BC\) (Mâu thuẫn với BĐT tam giác) => Loại (C).
Phương án D: \(3BC=6CA=8AB\Rightarrow BC=2CA=\frac{8}{3}AB\)
Hay \(BC=a,CA=\frac{a}{2},AB=\frac{3}{8}a\). Có \(CA+AB=\frac{a}{2}+\frac{3}{8}a=\frac{7}{8}a< a=BC\)
=> Mâu thuẫn với BĐT tam giác => Loại (D).
Phương án E: \(3BC=6CA=9AB\Rightarrow BC=2CA=3AB\)
Hay \(BC=a,CA=\frac{a}{2},AB=\frac{a}{3}\). Có \(CA+AB=\frac{a}{2}+\frac{a}{3}=\frac{5}{6}a< a=BC\)
=> Mâu thuẫn với BĐT tam giác => Loại (E).
Vậy chỉ có bộ số (A). (6,8,8) thỏa mãn đề.
Đúng 0
Bình luận (0)
Gọi a,b,c là 3 cạnh tương ứng với đường cao \(h_a;h_b;h_c\)
Có: \(a< b+c\Rightarrow\frac{2S}{h_a}< \frac{2S}{h_b}+\frac{2S}{h_c}\Rightarrow\frac{1}{h_a}< \frac{1}{h_b}+\frac{1}{h_c}\)
Tương tự với \(h_b;h_c\)
Xét: (B): (10;5;15) \(\frac{1}{5}>\frac{1}{10}+\frac{1}{15}=\frac{1}{6}\)(không là độ dài 3 đường cao)
Xét: (C): \(\frac{1}{2}=\frac{1}{4}+\frac{1}{4}\)(không là độ dài 3 đường cao)
Xét (D): \(\frac{1}{3}>\frac{1}{6}+\frac{1}{8}=\frac{7}{24}\)(không là độ dài 3 đường cao)
Xét: (E): \(\frac{1}{3}>\frac{1}{6}+\frac{1}{9}=\frac{5}{18}\)(không là độ dài 3 đường cao)
Chọn A
Đúng 0
Bình luận (0)
@ Tất Đạt@ Phương án B: Không phải là 5 đường cao. Nhìn nhầm :)). (1; 0,5; 1,5)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời