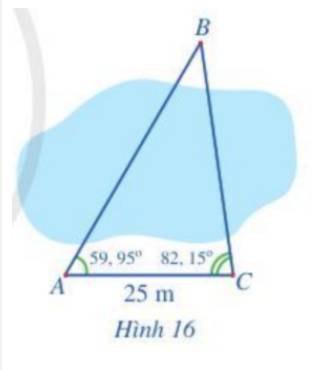
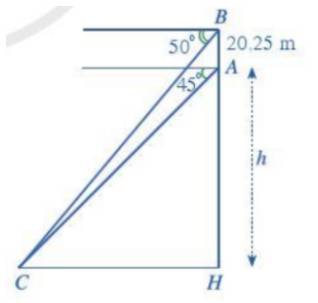
Áp dụng định lí cosin trong tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)\( \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \(AB = c = 5,{\rm{ }}AC = b = 6,{\rm{ }}BC = a = 7\).
\( \Rightarrow \cos A = \frac{{{6^2} + {5^2} - {7^2}}}{{2.5.6}} = \frac{1}{5}\)
Chú ý
Từ định lí cosin, ta suy cách tìm góc khi biết độ dài 3 cạnh
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\;\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\;\cos C = \frac{{{b^2} + {a^2} - {c^2}}}{{2ab}}.\)