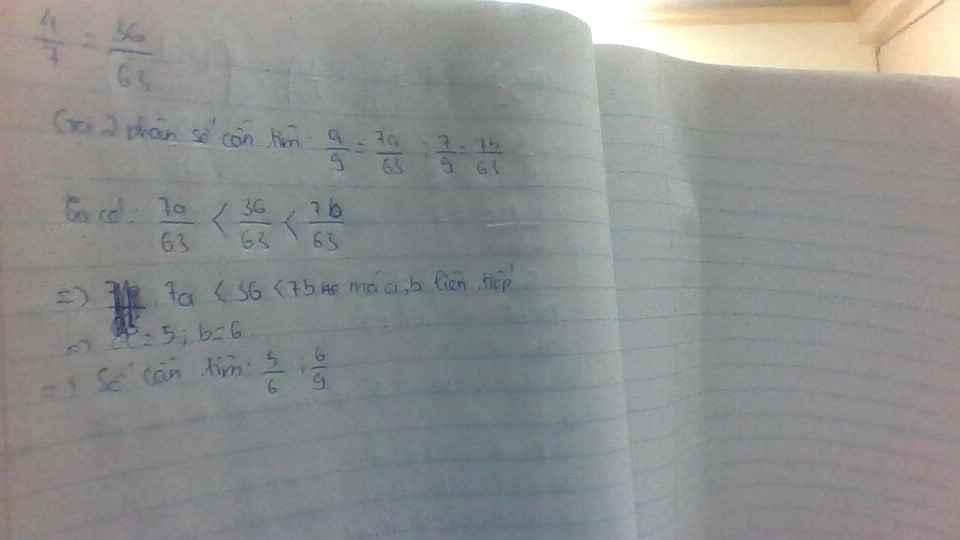biểu diễn các số -7;-6;-4,0,2,4 trên 1 trục số
LH
Những câu hỏi liên quan
Quan sát trục số sau:
![]()
a) Các điểm N, B, C biểu diễn những số nào?
b) Điểm nào biểu diễn số -7?
a) Điểm N biểu diễn số - 3
Điểm B biểu diễn số - 5
Điểm C biểu diễn số 3
b) Điểm biểu diễn số - 7 là điểm L.
Đúng 1
Bình luận (0)
Biểu diễn số thập phân: 253, 458, 1047, 3259 (2đ)
Biểu diễn có số nhị phân: 1011, 11011, 11101,1010 (2đ)
Biểu diễn các hệ số 16 (Hexa): 1AF, 2BD, 1BC, 2EF (2đ)
Chuyển đổi các hệ cơ số 10 sang cơ số 2: 7, 9, 21, 27 (2đ)
Chuyển đổi các hệ cơ số 10 sang hệ Hexa: 45,125, 235, 435 (2đ)
biểu diễn các số sau trên trục số-1/7,-7/3,3/2,9/2
tìm 2 PS có mẫu bằng 9,tử số là 2 số tự nhiền liên tiếp sao cho trục số điểm biểu diễn PS 4/7 nằm giữa các điểm biểu diễn của 2 PS cần tìm
Gọi tử số của phân số nhỏ hơn là x
Theo đề, ta có:
\(\dfrac{x}{9}< \dfrac{4}{7}< \dfrac{x+1}{9}\)
\(\Leftrightarrow\dfrac{7x}{63}< \dfrac{36}{63}< \dfrac{7x+7}{63}\)
Suy ra: x=5
Vậy: Hai phân số cần tìm là \(\dfrac{5}{9};\dfrac{2}{3}\)
Đúng 3
Bình luận (5)
Xác định các tập hợp sau và biểu diễn chúng trên trục số: (4; 7) ∩ (-7; -4)
4, tìm hai phân số có mẫu số bằng 9, tử số là hai số tự nhiên liên tiếp sao cho trên trục số điểm biểu diễn phân số 4/7 nằm giữa các điểm biểu diễn của hai phân số phải tìm.
\(\frac{4}{7}\) = \(\frac{4.9}{7.9}\) = \(\frac{36}{63}\)
Gọi 2 phân số cần tìm là : \(\frac{a}{9}\) = \(\frac{7a}{63}\) ; \(\frac{7}{9}\) = \(\frac{7b}{63}\) trong đó a;b là hai số tự nhiên liên tiếp
Theo đề bài : \(\frac{7a}{63}\) < \(\frac{36}{63}\) < \(\frac{7b}{63}\) -> 7a < 36 < 7b mà a;b liên tiếp -> a = 5 ; b = 6
Vậy phân số cần tìm là : \(\frac{5}{9}\) : \(\frac{6}{9}\)
:origin()/pre10/e83f/th/pre/f/2015/026/5/d/_2015_01_25__revekachibitopost_by_hyanna_natsu-d8fjo5q.png)
Đúng 0
Bình luận (0)
Hãy vẽ tia số và biểu diễn các số 7 và 11 trên tia số đó.
Mik cần gấp
tham khảo đây nhá
hãy vẽ tia số và biểu diễn các số 7 và 11 trên tia số đó bài 2
Đúng 2
Bình luận (0)
A)Biểu diễn các số nguyên sau trên cùng một trục số: 3,-5,-2
B)Sắp xếp các số nguyên sau theo thứ tự giảm dần: -7,2,-15,4,-3
C)Biểu diễn các số nguyên sau trên cùng một trục số:-3,2,-6
D) Sắp xếp các số nguyên sau theo thứ tự tăng dần:-6,5,-11, 7,-8
Biểu diễn các số hữu tỉ sau trên trục số: \( - \frac{1}{2};1;1,25;\frac{7}{4}\)