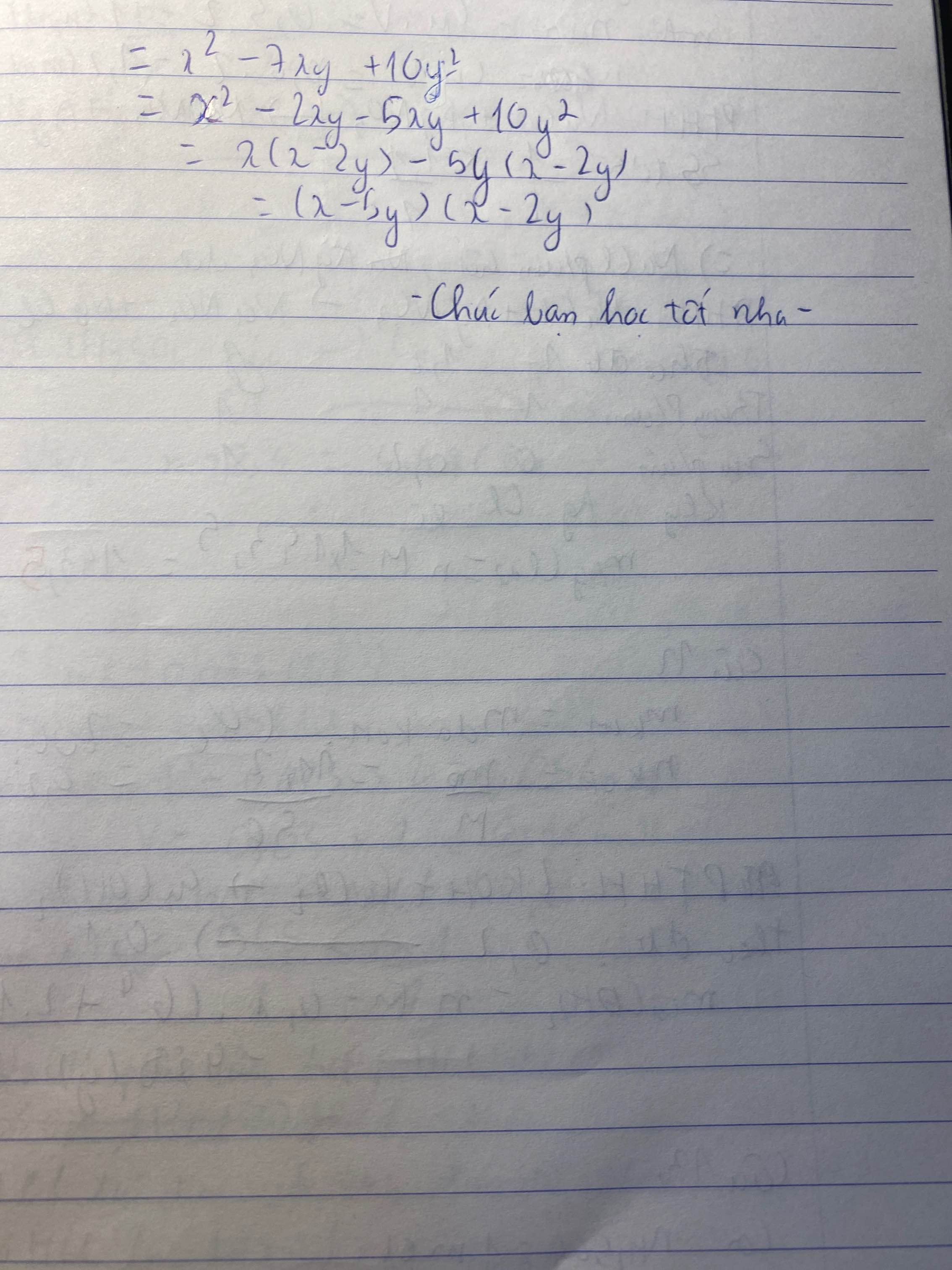Phân tích đa thức thành nhân tử : x^2 – xy(a + b) + aby^2
DN
Những câu hỏi liên quan
Phân tích đa thức thành nhân tử : (xy + 1)^2 – (x + y)^2
\(\left(xy+1\right)^2-\left(x+y\right)^2=\left(xy+1-x-y\right)\left(xy+1+x+y\right)=\left[x\left(y-1\right)-\left(y-1\right)\right]\left[x\left(y+1\right)+\left(y+1\right)\right]=\left(x-1\right)\left(y-1\right)\left(x+1\right)\left(y+1\right)\)
Đúng 2
Bình luận (0)
\(\left(xy+1\right)^2-\left(x+y\right)^2\)
\(=\left(xy-x-y+1\right)\left(xy+1+x+y\right)\)
\(=\left(y-1\right)\left(x-1\right)\left(y+1\right)\left(x+1\right)\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử:
(xy+1)^2 -(x+y)^2
Ta có: ( xy+1)^2 - (x+y)^2
= x^2.y^2 + 2xy + 1^2 - x^2 -2xy - y^2
= x^2. y^2 - x^2 - y^2 +1
= x^2( y^2 - 1) - (y^2 -1)
= (x^2 - 1)(y^2-1)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử
ab(x2+y2)+xy(a2+b2)
ab(x2+y2)+xy(a2+b2)
\(=abx^2+aby^2+a^2xy+b^2xy=\left(abx^2+a^2xy\right)+\left(aby^2+b^2xy\right).\)
\(=ax\left(bx+ay\right)+by\left(ay+bx\right)=\left(ax+by\right).\left(ay+bx\right)\)
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử :
a) 2x2-3x-2
b) x2+xy-y2
a) Đây là tam thức bạc 2
Để phân tích nó thành nhân tử được dễ dàng trước hết ta nhẩm nghiệm của nó
Nghiệm nhẩm là ước của hệ số tự do
Ở đây hệ số tự do là -2. Nhẩm ngay được 1 nghiệm của đa thức là 2. Vậy khi phân tích thành nhân tử đa thức chứa thừa số
x - 2.
Vậy bài này giải như sau:
2x2 -3x -2 = (2x2 -4x) + ( x- 2) = 2x( x-2) + (x-2) = (x-2) (2x+1)
b) Đây là đa thức có tính gần đối xứng hoặc đối xứng
Vì vậy đề bài của bạn bị sai rồi
Tất cả đều có phương pháp chung một cách dễ dàng,
Mình không thể diễn giải đầy đủ cho bạn phương pháp ở đây vì quá dài.
Nếu muốn bạn có thể gọi điện cho mình, mình sẽ hướng dẫn chi tiết cho. Bạn hãy nhắn tin vào hộp thư của mình nhé.
Mình nhắn lại SĐT cho.
Đúng 0
Bình luận (0)
a) 2x2-3x-2
=2x2_4x +x-2
=(2x2_ 4x)+(x-2)
=2x(x-2) +(x-2)
=(x-2) (2x+1)
Đúng 0
Bình luận (0)
Đa thức �2�+��2−�−�x2y+xy2−x−y được phân tích thành nhân tử là
(�−�)(��−1)(x−y)(xy−1).
(�−�)(��+1)(x−y)(xy+1).
(�+�)(��+1)(x+y)(xy+1).
(�+�)(��−1)(x+y)(xy−1)
Đọc tiếp
Đa thức được phân tích thành nhân tử là
. . .x²y + xy² - x - y
= (x²y + xy²) - (x + y)
= xy(x + y) - (x + y)
= (x + y)(xy - 1)
Đúng 2
Bình luận (0)
Phân tích đa thức thành nhân tử : (ab - 1)^2 + (a + b)^2
\(\left(ab-1\right)^2+\left(a+b\right)^2=a^2b^2-2ab+1+a^2+2ab+b^2=a^2+b^2+a^2b^2+1=a^2\left(b^2+1\right)+\left(b^2+1\right)=\left(a^2+1\right)\left(b^2+1\right)\)
Đúng 1
Bình luận (1)
\(\left(ab-1\right)^2+\left(a+b\right)^2=a^2b^2-2ab+1+a^2+2ab+b^2=a^2b^2+a^2+b^2+1=\left(a^2b^2+a^2\right)+\left(b^2+1\right)=a^2\left(b^2+1\right)+\left(b^2+1\right)=\left(a^2+1\right)\left(b^2+1\right)\)
Đúng 1
Bình luận (0)
\(\left(ab-1\right)^2+\left(a+b\right)^2\)
\(=a^2b^2+1+a^2+b^2\)
\(=\left(a^2+1\right)\left(b^2+1\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử : 4ab(a + x)(b + x)
\(=4ab\left(ab+ax+bx+x^2\right)=4a^2b^2+4a^2bx+4ab^2x+4abx^2\)
Đúng 2
Bình luận (1)
phân tích đa thức thành nhân tử
-7xy+x\(^2\)+10y\(^2\)
\(=x^2-2xy-5xy+10y^2=x\left(x-2y\right)-5y\left(x-2y\right)=\left(x-2y\right)\left(x-5y\right)\)
Đúng 2
Bình luận (0)
Phần tích đa thức thành nhân tử
A, x^2-3xy
B, (x+5)^2-9
C, xy+xz-2y-2z
A. x2 - 3xy
= x (x - 3y)
B. (x + 5)2 - 9
= (x + 5) - 32
= (x + 5 + 3) (x + 5 - 3)
= ( x + 8) ( x + 2)
C. xy + xz - 2y - 2z
= (xy + xz) - (2y + 2z)
= x (y + z) - 2 (y + z)
= (x - 2) (y + z)
Đúng 0
Bình luận (0)