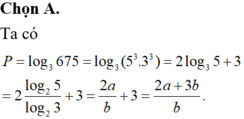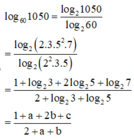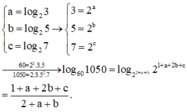cho log23=a, log25=b. tính log\(\sqrt{10}\)30
XM
Những câu hỏi liên quan
Cho
log
2
3
a
;
log
2
5
b
. Hãy tính
log
3
125
A.
b
3
a
B.
3
b
a
C. ...
Đọc tiếp
Cho log 2 3 = a ; log 2 5 = b . Hãy tính log 3 125
A. b 3 a
B. 3 b a
C. 2 a b
D. 2 b a
Ta có log 3 125 = 3 log 3 5
= 3 log 2 5 log 2 3 = 3 b a
Đáp án B
Đúng 0
Bình luận (0)
Cho
a
log
2
5
và
b
log
2
3
. Tính giá trị của biểu thức
P
log
3
675
theo a,b. A.
2
a
+
3
b
b
B.
2...
Đọc tiếp
Cho a = log 2 5 và b = log 2 3 . Tính giá trị của biểu thức P = log 3 675 theo a,b.
A. 2 a + 3 b b
B. 2 a b
C. a b + 3
D. 2 a b + 1
Ta có
P = log 3 675 = log 3 5 3 . 3 3 = 2 log 3 5 + 3 = 2 log 2 5 log 2 3 + 3 = 2 a b + 3 = 2 a + 3 b b
Đáp án A
Đúng 0
Bình luận (0)
Cho
a
log
2
5
và
b
log
2
3
Tính giá trị của biểu thức
P
log
3
675
theo a, b
A
.
2
a
+
3
b
b
B
.
...
Đọc tiếp
Cho a = log 2 5 và b = log 2 3 Tính giá trị của biểu thức P = log 3 675 theo a, b
A . 2 a + 3 b b
B . 2 a b
C . a b + 3
D . 2 a b + 1
log3sqrt{3}... , log100... , lne3... , log27 3... , logsqrt{3}3... , log0,125 2... , logsqrt[3]{49}7...,logdfrac{1}{125}5... , log8 4... , log25dfrac{1}{5}... , logdfrac{1}{5}sqrt{5}... , logdfrac{1}{7}sqrt[5]{49}... , log4 dfrac{1}{sqrt{2}}... , log27 3sqrt{3}...
Đọc tiếp
log3\(\sqrt{3}\)=... , log100=... , lne3=... , log27 3=... , log\(\sqrt{3}\)3=... , log0,125 2=... , log\(\sqrt[3]{49}\)7=...,
log\(\dfrac{1}{125}\)5=... , log8 4=... , log25\(\dfrac{1}{5}\)=... , log\(\dfrac{1}{5}\)\(\sqrt{5}\)=... , log\(\dfrac{1}{7}\)\(\sqrt[5]{49}\)=... , log4 \(\dfrac{1}{\sqrt{2}}\)=... , log27 \(3\sqrt{3}\)=...
\(log_3\sqrt{3}=log_33^{\dfrac{1}{2}}=\dfrac{1}{2}\)
\(lne^3=log_ee^3=3\)
\(log_{27}3=log_{3^3}3=\dfrac{1}{3}\)
\(\log_{\sqrt{3}}3=log_{3^{\dfrac{1}{2}}}3=1:\dfrac{1}{2}=2\)
\(\log_{0,125}2=log_{2^{-3}}2=\dfrac{1}{-3}\)
\(\log_{\sqrt[3]{49}}7=\log_{7^{\dfrac{2}{3}}}7=1:\dfrac{2}{3}=\dfrac{3}{2}\)
\(\log_{\dfrac{1}{125}}5=\log_{5^{-3}}5=-\dfrac{1}{3}\)
\(\log_84=log_{2^3}2^2=\dfrac{1}{3}\cdot2=\dfrac{2}{3}\)
\(\log_{25}\left(\dfrac{1}{5}\right)=\log_{5^2}5^{-1}=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}\)
\(\log_{\dfrac{1}{5}}\sqrt{5}=\log_{5^{-1}}5^{\dfrac{1}{2}}=\dfrac{1}{-1}\cdot\dfrac{1}{2}=-\dfrac{1}{2}\)
\(log_{\dfrac{1}{7}}\sqrt[5]{49}=\log_{7^{-1}}7^{\dfrac{2}{5}}=\dfrac{1}{-1}\cdot\dfrac{2}{5}=-\dfrac{2}{5}\)
\(\log_4\left(\dfrac{1}{\sqrt{2}}\right)=\log_{2^2}\left(\sqrt{2}\right)^{-1}\)
\(=\log_{2^{-2}}\left(\sqrt{2}\right)^{-\dfrac{1}{2}}=\dfrac{1}{-2}\cdot\dfrac{-1}{2}=\dfrac{1}{4}\)
\(\log_{27}3\sqrt{3}=\log_{3^3}3^{\dfrac{3}{2}}=\dfrac{1}{3}\cdot\dfrac{3}{2}=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Đặt
l
o
g
2
3
a
và
l
o
g
2
5
b
. Hãy biểu diễn P
l
o
g
3
240
theo a và b A. P
2
a
+
b
+
3
a
B. P ...
Đọc tiếp
Đặt l o g 2 3 = a và l o g 2 5 = b . Hãy biểu diễn P = l o g 3 240 theo a và b
A. P = 2 a + b + 3 a
B. P = a + b + 4 a
C. P = a + b + 3 a
D. P = a + 2 b + 3 a
Đặt
a
log
2
3
,
b
log
2
5
,
c
log
2
7
. Biểu thức biểu diễn
log
60
1050
theo a, b là A.
log
60
1050
1
+
a...
Đọc tiếp
Đặt a = log 2 3 , b = log 2 5 , c = log 2 7 . Biểu thức biểu diễn log 60 1050 theo a, b là
A. log 60 1050 = 1 + a + b + 2 c 1 + 2 a + b
B. log 60 1050 = 1 + a + 2 b + c 1 + 2 a + b
C. log 60 1050 = 1 + 2 a + b + c 2 + a + b
D. log 60 1050 = 1 + a + 2 b + c 2 + a + b
Đặt
a
log
2
3
,
b
log
2
5
,
c
log
2
7
. Biểu thức biểu diễn
log
60
1050
theo a,b,c chính xác là A.
log
60
1050
1
+...
Đọc tiếp
Đặt a = log 2 3 , b = log 2 5 , c = log 2 7 . Biểu thức biểu diễn log 60 1050 theo a,b,c chính xác là
A. log 60 1050 = 1 + a + 2 b + c 1 + 2 a + b .
B. log 60 1050 = 1 + a + 2 b + c 2 + a + b .
C. log 60 1050 = 1 + a + b + 2 c 1 + 2 a + b .
D. log 60 1050 = 1 + 2 a + b + c 2 + a + b .
Cho \(0 < a \ne 1\). Tính giá trị của biểu thức \(B = {\log _a}\left( {\frac{{{a^2} \cdot \sqrt[3]{a} \cdot \sqrt[5]{{{a^4}}}}}{{\sqrt[4]{a}}}} \right) + {a^{2{{\log }_a}\frac{{\sqrt {105} }}{{30}}}}\).
\(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}=\dfrac{a^2\cdot a^{\dfrac{1}{3}}\cdot a^{\dfrac{4}{5}}}{a^{\dfrac{1}{4}}}=\dfrac{a^{\dfrac{47}{15}}}{a^{\dfrac{1}{4}}}=a^{\dfrac{173}{60}}\)
\(\Rightarrow log_a\left(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}\right)=log_a\left(a^{\dfrac{173}{60}}\right)=\dfrac{173}{60}\)
\(a^{2log_a\left(\dfrac{\sqrt{105}}{30}\right)}=a^{log_a\left(\dfrac{7}{60}\right)}=\dfrac{7}{60}\)
Vậy \(B=\dfrac{173}{60}+\dfrac{7}{60}=\dfrac{180}{60}=3\)
Đúng 1
Bình luận (0)
Đặt
a
log
2
5
,
b
log
3
5
. Hãy biểu diễn log 6 5 theo a và b. A.
log
6
5
1
a
+
b
B.
log
6
5
a...
Đọc tiếp
Đặt a = log 2 5 , b = log 3 5 . Hãy biểu diễn log 6 5 theo a và b.
A. log 6 5 = 1 a + b
B. log 6 5 = a b a + b
C. log 6 5 = a 2 + b 2
D. log 6 5 = a + b