Cho a,b,c đôi một khác nhau (a#b#c) và \(\dfrac{a+b}{c}=\dfrac{b+c}{a}=\dfrac{c+a}{b}\)
Tính \(P=\left(1+\dfrac{a}{b}\right)\left(1+\dfrac{b}{c}\right)\left(1+\dfrac{c}{a}\right)\)
cho a,b,c khác 0 vá đôi một khác nhau thỏa mãn: (b+c)/(bc)=2/a. Chứng minh b/c=a-b/c-a
Cho a,b,c khác 0 và đôi một khác nhau thỏa mãn
b+c/bc=2/a.Chứng minh b/c=a-b/c-a
Cho ba số a,b,c đôi một khác nhau và khác 0 thỏa mãn : 1/c + 1/a-b = 1/a - 1/b-c. CMR: b = a+c
cho a,b,c là 3 số đôi một khác nhau CMR a/b-c+b/c-a+c/a-b=0
cho a,b,c là các số thực đôi một khác nhau
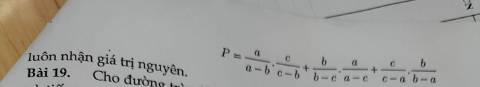
\(P=\dfrac{ab}{\left(a-c\right)\left(b-c\right)}+\dfrac{bc}{\left(b-a\right)\left(c-a\right)}+\dfrac{ca}{\left(c-b\right)\left(a-b\right)}\)
\(=\dfrac{ab\left(a-b\right)+bc\left(b-c\right)-ca\left(a-c\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{ab\left(a-b\right)+b^2c-bc^2-a^2c+ac^2}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{ab\left(a-b\right)-c\left(a-b\right)\left(a+b\right)+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{ab-c\left(a+b\right)+c^2}{\left(b-c\right)\left(a-c\right)}=\dfrac{ab-bc+c^2-ca}{\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{b\left(a-c\right)-c\left(a-c\right)}{\left(b-c\right)\left(a-c\right)}=\dfrac{\left(b-c\right)\left(a-c\right)}{\left(b-c\right)\left(a-c\right)}=1\)
cho a^3+b^3+c^3=3abc và a,b,c đôi một khác nhau. CMR a+b+c=0
\(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a^3+3a^2b+3ab^2+b^3\right)+c^3-3abc-3a^2b-3ab^2=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3abc\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ac-bc-ab\right)=0\)
\(\Leftrightarrow\frac{1}{2}\left(a+b+c\right)\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]=0\)
Vì a;b;c đôi 1 khác nhau nên \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ne0\)
\(\Rightarrow a+b+c=0\) (đpcm)
chuyển vế -> phân tích a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca) -> cm a2+b2+c2-ab-bc-ca >= 0
ta có: a2+b2+c2-ab-bc-ca >= 0 <=> 2a2+2b2+2c2-2ab-2bc-2ca >= 0 <=> (a2-2ab+b2)+(b2-2bc+c2)+(c2-2ca+a2) >=0
<=>(a-b)2+(b-c)2+(c-a)2 >=0
dấu "=" xảy ra khi a=b=c mà a,b,c đôi một khác nhau => a2+b2+c2-ab-bc-ca khác 0 <=> a+b+c=0
cho a,b,c khác không và đôi một khác nhau thõa mãn a^2(b+c)=b^2(a+c)=2013 . tính giá trị biểu thức H=c^2(a+b)
Cho a;b;c đôi một khác nhau. Tính giá trị biểu thức: P= a2/(a-b)(a-c) + b2/(b-c)(b-a) + c2/(c-b)(c-a)
\(P=\dfrac{a^2}{\left(a-b\right)\left(a-c\right)}+\dfrac{b^2}{\left(b-c\right)\left(b-a\right)}+\dfrac{c^2}{\left(c-b\right)\left(c-a\right)}\)
\(=\dfrac{a^2}{\left(a-b\right)\left(a-c\right)}+\dfrac{-b^2}{\left(b-c\right)\left(a-b\right)}+\dfrac{c^2}{\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{a^2\left(b-c\right)-b^2\left(a-c\right)+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{a^2b-a^2c-ab^2+b^2c+c^2a-bc^2}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)\(=\dfrac{ab\left(a-b\right)-c\left(a^2-b^2\right)+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{\left(a-b\right)\left(ab-c\left(a+b\right)+c^2\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=\dfrac{\left(a-b\right)\left[a\left(b-c\right)-c\left(b-c\right)\right]}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=1\)
Cho a,b,c khác 0 và khác nhau đôi một
Tính c2(a+b) biết b2(a+c)=a2(b+c)=2013
\(b^2\left(a+c\right)=a^2\left(b+c\right)=2013\)nên \(a^2b+a^2c-b^2a-b^2c=0\Leftrightarrow ab\left(a-b\right)+c\left(a-b\right)\left(a+b\right)=0\)
\(\Leftrightarrow\left(a-b\right)\left(ab+ca+bc\right)=0\Leftrightarrow ab+bc+ca=0\) vì \(a\ne b\ne c\ne0\)
\(\Leftrightarrow\left(ab+bc+ca\right)b=0\Leftrightarrow b^2\left(a+c\right)=-abc\)nên \(-abc=2013\)
\(\Leftrightarrow\left(ab+bc+ca\right)c=0\Leftrightarrow c^2\left(a+b\right)=-abc=2013\)
Có gì sai sót xin lượng thứ nha
1)Cho a,b,c đôi một khác nhau và khác 0,thoả mãn:(a+b)/c=(b+c)/a=(c+a)/b
Tính P=(1+a/b).(1+b/c).(1+c/a)
Câu hỏi của Chu Hoàng THủy Tiên - Toán lớp 7 - Học toán với OnlineMath