Cho 3x - y = 3z và 2x + y = 7z . Tính giá trị của biểu thức :
M = \(\dfrac{x^2-2xy}{x^2+y^2}\) ( x # 0 ; y # 0 )
TK
Những câu hỏi liên quan
Cho 3x-y=3z và 2x+y=7z. Tính giá trị của biểu thức: \(M=\dfrac{x^2-2xy}{x^2+y^2}\left(x\ne0,y\ne0\right)\)
Ta có: \(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Leftrightarrow3x-y+2x+y=10z\)
\(\Leftrightarrow5x=10z\)
hay x=2z
Thay x=2z vào biểu thức 3x-y=3z, ta được:
\(3\cdot2z-y=3z\)
\(\Leftrightarrow6z-y=3z\)
hay y=3z
Thay x=2z và y=3z vào biểu thức \(M=\dfrac{x^2-2xy}{x^2+y^2}\), ta được:
\(M=\dfrac{\left(2z\right)^2-2\cdot2z\cdot3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{13z^2}=\dfrac{-8z^2}{13z^2}=\dfrac{-8}{13}\)
Vậy: \(M=\dfrac{-8}{13}\)
Đúng 1
Bình luận (0)
\(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5x=10z\\3x-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\3.2z-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\y=3.2z-3z=6z-3z=3z\end{matrix}\right.\)
Có: \(M=\dfrac{x^2-2xy}{x^2+y^2}=\dfrac{\left(2z\right)^2-2.2z.3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{4z^2+9z^2}=\dfrac{-8z^2}{13z^2}==-\dfrac{8}{13}\)
Đúng 0
Bình luận (0)
\(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5x=10z\\3x-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\3.2z-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\y=3.2z-3z=6z-3z=3z\end{matrix}\right.\)
Có: \(M=\dfrac{x^2-2xy}{x^2+y^2}=\dfrac{\left(2z\right)^2-2.2z.3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{4z^2+9z^2}=\dfrac{-8z^2}{13z^2}==-\dfrac{8}{13}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho 3x-y=3z và 2x+y=7z. Tính giá trị của biểu thức:
M=\(\frac{x^2-2xy}{x^2+y^2}\)
\(3x-y=3z\Rightarrow-y=3z-3x\Rightarrow y=3x-3z\)
\(2x+y=7z\Rightarrow y=7z-2x\)\(\Rightarrow3x-3z=7z-2x=y\Rightarrow3x-3z-7z+2x=5x-10z=0\Rightarrow x-2z=0\Rightarrow x=2z\)
\(2x+y=7z\Rightarrow2\cdot2z+y=7z\Rightarrow4z+y=7z\Rightarrow y=3z\)
\(M=\frac{x^2-2xy}{x^2+y^2}=\frac{\left(2z\right)^2-2\cdot2z\cdot3z}{\left(2z\right)^2+\left(3z\right)^2}=\frac{4z^2-12z^2}{4z^2+9z^2}=-\frac{8z^2}{13z^2}=-\frac{8}{13}\)
Đúng 0
Bình luận (0)
Cho 3x-y=3z và 2x+y=7z. Tính giá trị biểu thức \(M=\frac{x^2-2xy}{x^2+y^2}\)
ta có 5x=10z=> x=2z=> y=3z
Tháy vào, ta có \(M=\frac{4z^2-12z^2}{4z^2+9z^2}=\frac{-8z^2}{13z^2}=-\frac{8}{13}\)
Đúng 0
Bình luận (0)
Ta có:
\(3x-y+2x+y=3z+7z\)
\(5x=10z\)
\(x=2z\)
thay:\(4z+y=7z\) \(\Rightarrow y=3z\)
Thay vào M ta đc:M=\(\frac{4z^2-12z^2}{4z^2+9z^2}\) =\(\frac{-8z^2}{13z^2}=\frac{-8}{13}\)
vậy\(M=\frac{-8}{13}\) nếu\(3x-y=3z;2x+y=7z\)
Đúng 0
Bình luận (0)
cho 3x-y=3z và 2+y=7z. Tính giá trị của biểu thức \(M=\frac{x^2-2xy}{x^2+y^2}\)(x khác 0,y khác 0)
Mình sửa lại đề cho đúng nhé
\(\hept{\begin{cases}3x-y=3z\\2x+y=7z\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2z\\y=3z\end{cases}}\)
Thế vô M ta được
Đúng 0
Bình luận (0)
\(M=\frac{x^2-2xy}{x^2+y^2}=\frac{4z^2-2.2z.3z}{4z^2+9z^2}=-\frac{8}{13}\)
Đúng 0
Bình luận (0)
\(_{\hept{\begin{cases}3x-y=3z\left(1\right)\\\\2x+y=7z\end{cases}\Rightarrow}\left(3x-y\right)+\left(2x+y\right)=10z}\)
\(\Leftrightarrow\)5x=10z\(\Leftrightarrow x=2z\)
thay x=2z vào (1) ta được :6z+y=3z\(\Rightarrow y=6z-3z=3z\)
thay y=3z,x=2z vào biểu thức M=\(\frac{4z^2-12z^2}{4z^2+9z^2}=\frac{-8}{13}\)
Đúng 0
Bình luận (0)
cho 3x-y=3z và 2x+y=7z
tính giá trị biểu thức
P=\(\frac{x^2-2xy}{x^2+y^2}\)với x và y khác 0
Cho tỉ lệ thức \(\dfrac{x}{y}=\dfrac{2}{3}\). Tính giá trị của các biểu thức sau:
\(A=\dfrac{x+5y}{3x-2y}-\dfrac{2x-3y}{4x+5y}\)
\(B=\dfrac{2x^2-xy+3y^2}{3x^2+2xy+y^2}\)
Lời giải:
$\frac{x}{y}=\frac{2}{3}\Rightarrow \frac{x}{2}=\frac{y}{3}$. Đặt $\frac{x}{2}=\frac{y}{3}=k$ thì:
$x=2k; y=3k$
Khi đó: $3x-2y=3.2k-3.2k=0$. Mẫu số không thể bằng $0$ nên $A$ không xác định. Bạn xem lại.
$B=\frac{2(2k)^2-2k.3k+3(3k)^2}{3(2k)^2+2.2k.3k+(3k)^2}=\frac{29k^2}{33k^2}=\frac{29}{33}$
Đúng 2
Bình luận (0)
Cho 3x – y = 3z và 2x + y = 7z. Tính giá trị của biểu thức M = x 2 - 2 x y x 2 + y 2
Từ 3x – y = 3z và 2x + y = 7z ⇒ x = 2z; y = 3z. Thay vào M ta được
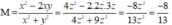
Đúng 0
Bình luận (0)
Cho biểu thức M=\(x^3\)+3x\(y^2\)- 2xy+\(x^3\)- xy - 2x\(y^2\)+1
a) thu gọn biểu thức M ; tính giá trị biểu thức khi x=-1 ; y=2
A = 3x^3 +6x^2 + 3xy^3
x= 1 phần 2 ; p = -1 phần 3
A=3.1 phần 2^3 . -1 phần 3 + 6.(1 phần 2)^2 . (-1 Phần 3)^2+3 1 phần 2 . (-1 phần 3)^3
=-1 phần 8 + -1 phần 2 - 1 phần 2
= -1 phần 4
Đúng 0
Bình luận (0)
Tính giá trị nhỏ nhất của biểu thức
P=X^2 + Y^2 + XY + X + Y
Q=X^2 + XY + Y^2 - 3X - 3Y + 2017
F=X^2 + 2Y^2 + 3Z^2 - 2XY + 2XZ - 2X - 2Y - 8Z + 1998
M=(X+1)^2 + (X-3)^2 + (Y-2)^2 + 4





