trong các cặp tam giác dưới đây có những tam giác nào bằng nhau
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
Trong các tam giác dưới đây có những tam giác nào bằng nhau? Vì sao?
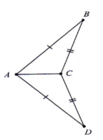
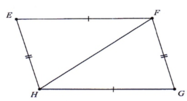
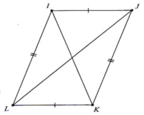
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)
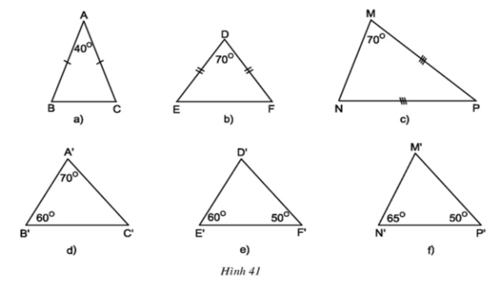
- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A
Mà ΔABC cân tại A ⇒ ∠B = ∠C
⇒∠B = ∠C = ( 180o- 40o)/2 = 70o
ΔMNP cân tại P ⇒ ∠M = ∠N = 70o
ΔABC và ΔPMN có
∠B = ∠M = 70o)
∠C = ∠N = 70o)
⇒ ΔABC ∼ ΔPMN (g.g)
- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o
⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o
ΔA’B’C’ và ΔD’E’F’ có
∠B' = ∠E' (= 60o)
∠C' = ∠F' (= 50o)
⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)
Đúng 0
Bình luận (0)
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)
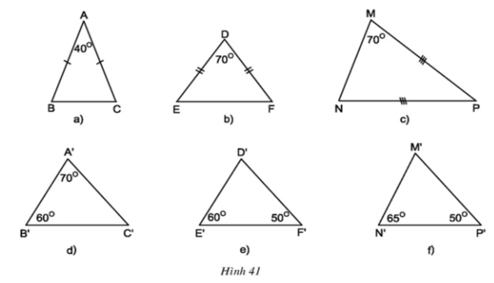
- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A
Mà ΔABC cân tại A ⇒ ∠B = ∠C
⇒∠B = ∠C = ( 180o- 40o)/2 = 70o
ΔMNP cân tại P ⇒ ∠M = ∠N = 70o
ΔABC và ΔPMN có
∠B = ∠M = 70o)
∠C = ∠N = 70o)
⇒ ΔABC ∼ ΔPMN (g.g)
- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o
⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o
ΔA’B’C’ và ΔD’E’F’ có
∠B' = ∠E' (= 60o)
∠C' = ∠F' (= 50o)
⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)
Đúng 0
Bình luận (0)
Câu 1: Khẳng định nào sau đây là đúng?A. Hai tam giác có các góc tương ứng bằng nhau là hai tam giác bằng nhau.B. Hai tam giác có hai cặp góc tương ứng bằng nhau là hai tam giác bằng nhau.C. Hai tam giác có các góc tương ứng bằng nhau, các cạnh tương ứng bằng nhau là hai tam giác bằng nhau.D. Hai tam giác có chu vi bằng nhau là hai tam giác bằng nhau.Câu 2: Cho DABC DIHK . Biết AB 6cm, HK 5cm, CA 8cm . Chu vi của ∆ABC bằngA. 15 cm. B. 17 cm. C. 19 cm. D. 20 cm.Câu 3: Cho tam giác ABC có chu...
Đọc tiếp
Câu 1: Khẳng định nào sau đây là đúng?
A. Hai tam giác có các góc tương ứng bằng nhau là hai tam giác bằng nhau.
B. Hai tam giác có hai cặp góc tương ứng bằng nhau là hai tam giác bằng nhau.
C. Hai tam giác có các góc tương ứng bằng nhau, các cạnh tương ứng bằng nhau là hai tam giác bằng nhau.
D. Hai tam giác có chu vi bằng nhau là hai tam giác bằng nhau.
Câu 2: Cho DABC = DIHK . Biết AB = 6cm, HK = 5cm, CA = 8cm . Chu vi của ∆ABC bằng
A. 15 cm. B. 17 cm. C. 19 cm. D. 20 cm.
Câu 3: Cho tam giác ABC có chu vi bằng 24cm, dài cạnh EF bằng
AB = 8cm và
AC : BC = 5 : 3 . Biết DABC = DDEF . Độ
A. EF = 9cm . B.
EF = 6cm . C. EF = 8cm . D.
EF = 10cm .
Câu 4: Cho hai tam giác ABC và PQR bằng nhau. Biết tam giác ABC bằng
AB = 8cm, BC = 5cm, PR = 2.QR . Chu vi của
A. 18 cm. B. 23 cm. C. 20 cm. D. 21 cm.
Tam giác nào trong các tam giác dưới đây có trọng tâm, trực tâm trùng nhau.
A. Tam giác vuông
B. Tam giác cân
C. Tam giác đều
D. Tam giác tù
Hãy chỉ ra các cặp tam giác vuông bằng nhau dưới đây.
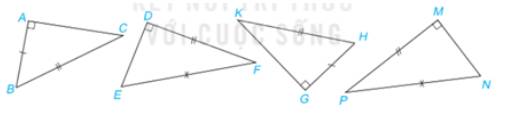
Xét hai tam giác ABC vuông tại A và GHK vuông tại G có:
AB = GH (gt)
BC = HK (gt)
Do đó ΔABC=ΔGHK (cạnh huyền – cạnh góc vuông).
Xét hai tam giác DEF vuông tại D và MNP vuông tại M có:
DF = MP (gt)
EF = NP (gt)
Do đó ΔDEF=ΔMNP (cạnh huyền – cạnh góc vuông).
Vậy ΔABC=ΔGHK, ΔDEF=ΔMNP.
Đúng 0
Bình luận (0)
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.
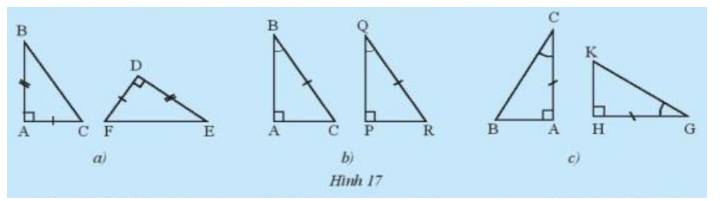
a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:
AB = DE (gt)
\(\widehat {BAC} = \widehat {EDF}\) (gt)
AC = DF (gt)
\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) (c-g-c)
b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)
Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)
Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:
\(\widehat C = \widehat R\) (gt)
BC = QR (gt)
\(\widehat B = \widehat Q\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) (g-c-g)
c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:
\(\widehat C = \widehat G\) (gt)
AC = HG (gt)
\(\widehat A = \widehat H\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) (g-c-g)
Đúng 0
Bình luận (0)
cho hình tam giác ABCD ( AB và DC là đáy ) AC và AB gặp nhau ở M . hỏi trong hình đó có những cặp tam giác nào có diện tích bằng nhau
k cần vẽ hình đâu giải hộ mình là được rồi
Đúng 0
Bình luận (0)
tự vẽ mình k biets vẽ hình kiểu gf cả , ở giấy rồi mình chỉ ở máy tính k biết giải kiểu gì
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang vuông ABCD. Hai đường chéo cắt nhau tại I. Điểm E nằm dưới cạnh DC, tam giác DEC có chiều cao bằng chiều cao hình thang.
A) Trong hình thang ABCD có những hình tam giác nào có diện tích bằng nhau?
B) Tìm những tam giác có diện tích bằng diện tích hình tam giác DEC


