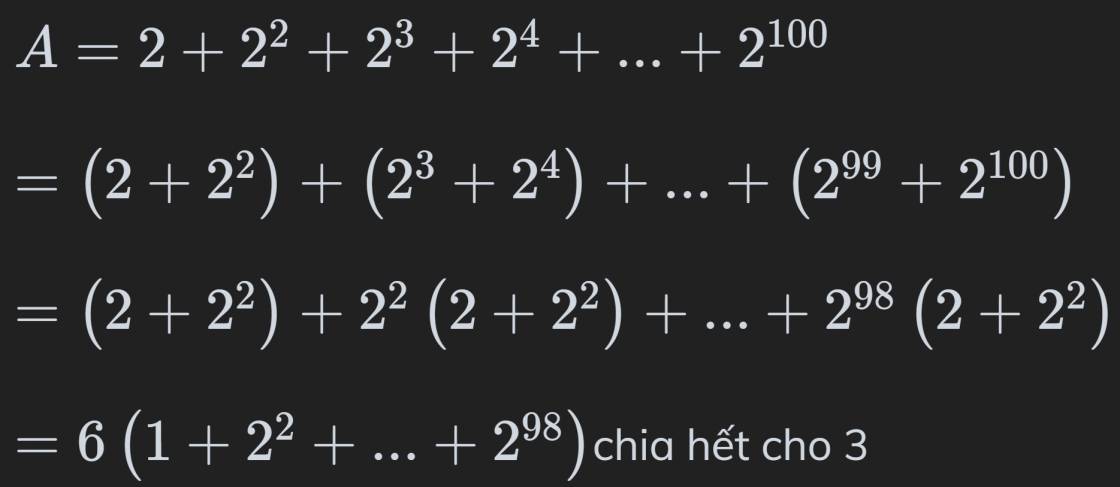CMR A=5+51+52+53+..........+599+5100 chia hết cho 6
LG
Những câu hỏi liên quan
Cho S = 1 - 5 + 52 - 53 +.... + 598 - 599
a)Tính S b)CMR: 5100 chia cho 6 dư 1
0\(a.S=1-5+5^2-5^3+...+5^{98}-5^{99}\\ 5S=5-5^2+5^3-5^4+.....+5^{99}-5^{100}\\ 5S+S=\left(5-5^2+5^3-5^4+.....+5^{99}-5^{100}\right)+\left(1-5^{ }+5^2-5^3+.....+5^{98}-5^{99}\right)\\ 6S=1-5^{100}\\ S=\dfrac{1-5^{100}}{6}\\ \)
\(b,S6=1-5^{100}\\ 1-S6=5^{100}\)
=> 5100 chia 6 du 1
Đúng 3
Bình luận (0)
e đang cần gấp, có ai đến giúp e ko?
Đúng 0
Bình luận (0)
\(S=1-5+5^2-5^3+...+5^{98}-5^{99}\\ a,S=5^0.\left(1-5\right)+5^2.\left(1-5\right)+...+5^{98}.\left(1-5\right)=-4.\left(5^0+5^2+5^4+...+5^{98}\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Ta có: A 5 + 52 + 53 +....+ 5100
⇒A(5+52)+(53+54)+...+(599+5100)⇒A(5+52)+(53+54)+...+(599+5100)
⇒A5(1+5)+53.(1+5)+...+599.(1+5)⇒A5(1+5)+53.(1+5)+...+599.(1+5)
⇒A5.6+53.6+...+599.6⇒A5.6+53.6+...+599.6
A6.(5+53+...+599)A6.(5+53+...+599) chia hết
Ta có: A 5 + 52 + 53 +....+ 5100
⇒A(5+52)+(53+54)+...+(599+5100)⇒A(5+52)+(53+54)+...+(599+5100)
⇒A5(1+5)+53.(1+5)+...+599.(1+5)⇒A5(1+5)+53.(1+5)+...+599.(1+5)
⇒A5.6+53.6+...+599.6⇒A5.6+53.6+.....
Đọc tiếp
Ta có: A = 5 + 52 + 53 +....+ 5100
chia hết
Ta có: A = 5 + 52 + 53 +....+ 5100
Đề bài thiếu yêu cầu cụ thể em nhé. em cập nhật lại câu hỏi để được sự hỗ trợ tốt nhất cho tài khoản olm vip
Đúng 0
Bình luận (0)
1)Cho S = 1 - 5 + 52 - 53 + ... + 598 - 599
a) Tính S
b) CMR : 5100 chia cho 6 dư 1
Bài 1:
a: \(S=1-5+5^2-5^3+...+5^{98}-5^{99}\)
=>\(5S=5-5^2+5^3-5^4+...+5^{99}-5^{100}\)
=>\(6S=5-5^2+5^3-5^4+...+5^{99}-5^{100}+1-5+5^2-5^3+...+5^{98}-5^{99}\)
=>\(6S=-5^{100}+1\)
=>\(S=\dfrac{-5^{100}+1}{6}\)
b: S=1-5+52-53+...+598-599 là số nguyên
=>\(\dfrac{-5^{100}+1}{6}\in Z\)
=>\(-5^{100}+1⋮6\)
=>\(5^{100}-1⋮6\)
=>\(5^{100}\) chia 6 dư 1
Đúng 3
Bình luận (0)
bài 6:
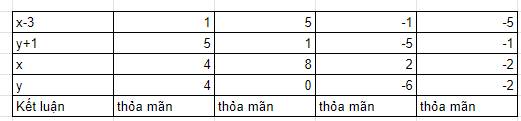
a) Tìm cặp số x,y nguyên biết: (x - 3).(y+1)=5
b) Cho A = 21 + 5 + 52 + 53 + ... + 599.Tìm số dư của phép chia khi lấy A chia cho 6
Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.
Đúng 2
Bình luận (0)
Cho S = 1/51 + 1/52 + 1/53 + ... + 1/100 . CMR 7/12 < S < 5/6
Cho a/b=1/51+1/52+1/53+...+1/100
CMR a chia hết cho 151
Các bạn nhanh nhé mik cần gấp
Ai đúng mik tick cho
\(\frac{a}{b}=\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+...+\frac{1}{100}\)
\(\frac{a}{b}=\left(\frac{1}{51}+\frac{1}{100}\right)+\left(\frac{1}{52}+\frac{1}{99}\right)+...+\left(\frac{1}{75}+\frac{1}{76}\right)\)
\(\frac{a}{b}=\frac{151}{51.100}+\frac{151}{50.99}+...+\frac{151}{75.76}\)
Chọn mẫu chung = 51.52.53...100
Gọi các thừa số phụ lần lượt là: k1; k2; ...; k25
=> \(\frac{a}{b}=\frac{151.\left(k_1+k_2+...+k_{25}\right)}{51.52...100}\)
Do 151 là số nguyên tố mà tích 51.52...100 không chứa thừa số 151 => 51.52....100 không chia hết cho 151
=> đến khi phân số a/b tối giản thì a vẫn chia hết cho 151 (đpcm)
Đúng 0
Bình luận (0)
Mik rút gọn cho bn nha
\(\frac{a}{b}=\frac{1}{51.100}+\frac{1}{52.99}+..........+\frac{1}{100.51}\)
\(151.\frac{a}{b}=\frac{1}{51}+\frac{1}{100}+\frac{1}{52}+\frac{1}{99}+......+\frac{1}{100}+\frac{1}{51}\)
\(\Rightarrow\left(151.\frac{a}{b}\right):2=\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+.........+\frac{1}{100}\)
\(\Rightarrow\frac{a}{b}=\frac{2}{151}.\left(\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+.........+\frac{1}{100}\right)\)
Chúc bn hok tốt
Đúng 0
Bình luận (0)
a) Chứng minh: B = 31 + 32 + 33 + 34 + … + 32010 chia hết cho 4.
b) Chứng minh: C = 51 + 52 + 53 + 54 + … + 52010 chia hết cho 31.
c) Cho S=17+52+53+54+ ... +52010 . Tìm số dư khi chia S cho 31.
\(B=3+3^2+3^3+3^4+...+3^{2009}+3^{2010}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)
\(=4.\left(3+3^3+...+3^{2009}\right)\)
⇒ \(B\) ⋮ 4
Đúng 3
Bình luận (0)
b: \(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)=31\cdot\left(5+...+5^{2008}\right)⋮31\)
Đúng 2
Bình luận (0)
a. Chứng minh A=21+22+23+24+...+2100 chia hết cho 3
b. Chứng minh B=31+32+33+34+...+299chia hết cho 13
c. Chứng minh C=51+52+53+54+...+5105 chia hết cho 6 và 31
điền chữ số thích hợp vào dấu * để :
1) *45* chia hết cho 2;3;5;9
2)*1*8 chia hết cho 2;3;9
3)2025+*36 chia hết cho 3
4)125+5100+31* chia hết cho 5
5)202210+420+53* chia hết cho 2
6)37*+*23 chia hết cho 3
1, \(\overline{a45b}\) \(⋮\) 2; 3; 5; 9
⇒ b = 0; a + 4 + 5 + b ⋮ 9 ⇒ a + 9 ⋮ 9 ⇒ a = 9
Vậy \(\overline{a45b}\) = 9450
2, \(\overline{a1b8}\) \(⋮\) 2;3;9 ⇔ a + 1 + b + 8 ⋮ 9 ⇒ a + b ⋮ 9
⇒ b = 0; 1; 2; 3; 4; 5; 6; 7; 8
a = 9; 8; 7; 6; 5; 4; 3; 2; 1
\(\Rightarrow\) \(\overline{a1b8}\) = 9108; 8118; 7128; 6138; 5148; 4158; 3168; 2178; 1188
Đúng 2
Bình luận (0)
3, 2025 + \(\overline{a36}\) \(⋮\) 3
⇔ 2 + 0 + 2 + 5 + a + 3 + 6 ⋮ 3
18 + a ⋮ 3
a ⋮ 3
a = 0; 3; 6; 9
4, 125 + 5100 + \(\overline{31a}\) ⋮ 5
⇔ \(\overline{31a}\) ⋮ 5
a ⋮ 5
a = 0; 5
Đúng 2
Bình luận (0)
1) \(\overline{x45y}⋮2;3;5;9\)
\(\Rightarrow y=0\left(⋮2;5\right)\)
\(x+4+5+0⋮\left(3;9\right)\)
\(\Rightarrow x=9\)
\(\Rightarrow\overline{x45y}=9450\)
3) \(2025+\overline{x36}⋮3\)
mà \(2025⋮3\)
\(\Rightarrow\overline{x36}⋮3\)
\(\Rightarrow x+3+6⋮3\)
\(\Rightarrow x\in\left\{3;6;9\right\}\)
3) \(2022^{10}+4^{20}+\overline{53x}⋮2\)
\(2022^{10}=2022^8.2022^2=\overline{.....6}x\overline{....4}=\overline{.....4}⋮2\)
\(4^{20}=\overline{.....6}⋮2\)
\(\Rightarrow\overline{53x}⋮2\)
\(\Rightarrow x\in\left\{0;2;4;6;8\right\}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng:
a) A = 3 + 33 + 33 + ...+ 399 chia hết cho 13
b) B = 5 + 52 + 53 + ... + 550 chia hết cho 6
Sửa câu a
a)Ta có:
\(A=3+3^2+3^3+...+3^{99}\)
\(A=\left(3+3^2+3^3\right)+...+\left(3^{97}+3^{98}+3^{99}\right)\)
\(A=\left(3+3^2+3^3\right)+...+3^{96}.\left(3+3^2+3^3\right)\)
\(A=39+...+3^{96}.39\)
\(A=39.\left(1+...+3^{96}\right)\)
Vì 39 \(⋮\) 13 nên 39 . ( 1 + ... + 396 ) \(⋮\) 13
Vậy A \(⋮\) 13
_________
b)Ta có:
\(B=5+5^2+5^3+...+5^{50}\)
\(B=\left(5+5^2\right)+\left(5^3+5^4\right)+...+\left(5^{49}+5^{50}\right)\)
\(B=\left(5+5^2\right)+5^2.\left(5+5^2\right)+...+5^{48}.\left(5+5^2\right)\)
\(B=30+5^2.30+...+5^{48}.30\)
\(B=30.\left(1+5^2+...+5^{48}\right)\)
Vì 30 \(⋮\) 6 nên 30. ( 1 + 52 + ... + 548 ) \(⋮\) 6
Vậy B \(⋮\) 6
Đúng 2
Bình luận (0)
a,A=3+32+33+..+399=(3+32+33)+...+(397+398+399)
=3(1+3+32)+...+397(1+3+32)=3x13+...+397x13=13(3+...+97)⋮13
b,B=5+52+...+550=(5+52)+...+(549+550)=5(1+5)+..+549(1+5)
=5x6+...+549x6=6(5+..+549)⋮6.
Đúng 1
Bình luận (0)