Cho M là tập hợp các số tự nhiên có ba chữ số ghép từ các chữ số : 2; 3; 5; 9. Tính số phần tử của tập hợp M.
NT
Những câu hỏi liên quan
a) Tìm ab . Biết 1ab + 36 =ab1
b) Cho M là tập hợp các số tự nhiên có ba chữ số ghép từ các chữ số: 2; 3; 5; 9. Tính số phần tử của tập hợp M.
Cho tập hợp A của các số tự nhiên có 2 chữ số mà tổng các chữ số là 7 và B là tập hợp của các số tự nhiên có hai chữ số lập nên từ hai trong ba chữ số 0;2;5.Viết các tập hợp A,B dưới dạng liệt kê các phần tử và tìm tập hợp các phần tử chung của cả hai tập hợp.
ong số học, bội số chung nhỏ nhất (hay còn gọi tắt là bội chung nhỏ nhất, viết tắt là BCNN, tiếng Anh: least common multiple hoặc lowest common multiple (LCM) hoặc smallest common multiple) của hai số nguyên a và b là số nguyên dương nhỏ nhất chia hết cho cả a và b.[1] Tức là nó có thể chia cho a và b mà không để lại số dư. Nếu a hoặc b là 0, thì không tồn tại số nguyên dương chia hết cho a và b, khi đó quy ước rằng LCM(a, b) là 0.
Định nghĩa trên đôi khi được tổng quát hoá cho hơn hai số nguyên dương: Bội chung nhỏ nhất của a1,..., an là số nguyên dương nhỏ nhất là bội số của a1,..., an.
Đúng 0
Bình luận (0)
Cho tập hợp A của các số tự nhiên có 2 chữ số mà tổng các chữ số là 7 và B là tập hợp của các số tự nhiên có hai chữ số lập nên từ hai trong ba chữ số 0;2;5.Viết các tập hợp A,B dưới dạng liệt kê các phần tử và tìm tập hợp các phần tử chung của cả hai tập hợp.
A = {20;50}
B = {20; 25; 52; 50}
AB = {20; 50}
Đúng 0
Bình luận (0)
+) Ta có : 7 = 7 + 0 = 0 + 7 = 1 + 6 = 6 + 1 = 5 + 2 = 2 + 5 = 3 + 4 = 4 + 3
=> Các số tự nhiên có 2 chữ số mà tổng của nó bằng 7 là 70 ; 16 ; 61 ; 25 ; 52 ; 34 ; 43
Vậy A = { 16 ; 25 ; 34 ; 43 ; 52 ; 61; 70 }
+) Các số tự nhiên lập từ ba chữ số 0 ; 2 ; 5 là 20 ; 25 ; 50 ; 52
=> B = { 20 ; 25 ; 50 ; 52 }
Phần tử chung của cả 2 tập hợp trên là 25 và 52
Đúng 0
Bình luận (1)
Gọi M là tập hợp các số tự nhiên có ba chữ số lập được từ các chữ số 0,1,2,3,4,5,6,7 . Lấy ngẫu nhiên đồng thời 2 số từ tập M . Xác suất để cả 2 số lấy được đều có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và hàng đơn vị là
b.1) Tập hợp các số tự nhiên có hai chữ số trong đó chữ số hàng chục hơn chữ số hàng đơn vị là 1.b.2) Tập hợp các số tự nhiên có hai chữ số trong đó hiệu chữ số hàng chục và chữ số hàng đơn vị là 4.c. Cho ba số 0;2;3. Viết tập hợp các số tự nhiên có hai chữ số lập được từ ba số đã cho.d. Cho là tập hợp các số tự nhiên chia hết cho 5 và nhỏ hơn 25. Viết tập hợp bằng hai cách.
Đọc tiếp
b.1) Tập hợp ![]() các số tự nhiên có hai chữ số trong đó chữ số hàng chục hơn chữ số hàng đơn vị là 1.
các số tự nhiên có hai chữ số trong đó chữ số hàng chục hơn chữ số hàng đơn vị là 1.
b.2) Tập hợp ![]() các số tự nhiên có hai chữ số trong đó hiệu chữ số hàng chục và chữ số hàng đơn vị là 4.
các số tự nhiên có hai chữ số trong đó hiệu chữ số hàng chục và chữ số hàng đơn vị là 4.
c. Cho ba số 0;2;3. Viết tập hợp ![]() các số tự nhiên có hai chữ số lập được từ ba số đã cho.
các số tự nhiên có hai chữ số lập được từ ba số đã cho.
d. Cho ![]() là tập hợp các số tự nhiên chia hết cho 5 và nhỏ hơn 25. Viết tập hợp
là tập hợp các số tự nhiên chia hết cho 5 và nhỏ hơn 25. Viết tập hợp ![]() bằng hai cách.
bằng hai cách.
Tập các số tự nhiên chẵn từ số chẵn a đến số chẵn b có bao nhiêu phần tử?Tập hợp A gồm các số tự nhiên sao cho x + 5 12. Hỏi tập hợp A có bao nhiêu phần tử?Tập hợp B gồm các số tự nhiên sao cho x - 7 21. Hỏi tập hợp B có bao nhiêu phần tử?Tập hợp D gồm các số tự nhiên sao cho x . 0 10. Hỏi tập hợp D có bao nhiêu phần tử?Tập các số tự nhiên lẻ từ số lẻ a đến số lẻ b có bao nhiêu phần tử?Cho A là tập hợp các số có ba chữ số được tạo thành bởi ba chữ số 0 , 5 , 8 và mỗi chữ số chỉ xuất hiện một...
Đọc tiếp
Tập các số tự nhiên chẵn từ số chẵn a đến số chẵn b có bao nhiêu phần tử?
Tập hợp A gồm các số tự nhiên sao cho x + 5 = 12. Hỏi tập hợp A có bao nhiêu phần tử?
Tập hợp B gồm các số tự nhiên sao cho x - 7 = 21. Hỏi tập hợp B có bao nhiêu phần tử?
Tập hợp D gồm các số tự nhiên sao cho x . 0 = 10. Hỏi tập hợp D có bao nhiêu phần tử?
Tập các số tự nhiên lẻ từ số lẻ a đến số lẻ b có bao nhiêu phần tử?
Cho A là tập hợp các số có ba chữ số được tạo thành bởi ba chữ số 0 , 5 , 8 và mỗi chữ số chỉ xuất hiện một lần. Tập hợp A có bao nhiêu tập hợp con?
có 1 phần tử
A={7}có 1 phần tử
B là tập hợp rỗng
D là tập hợp rỗng
có 1 phần tử
tập hợp A có 4 tập hợp con
Đúng 0
Bình luận (0)
câu 1 cho A là tập hợp các số có hai chữ số khác nhau có bao nhiêu cách chọn ngẫu nhiên ba số từ tập a
câu 2 cho A là tập hợp các số có ba chữ số khác nhau có bao nhiêu cách chọn ngẫu nhiên hai số từ tập a
Câu 1:
Gọi số tổng quát là \(X=\overline{ab}\)
a có 9 cách chọn
b có9 cách chọn
=>Có 9*9=81(số)
Số cách chọn ngẫu nhiên 3 số từ tập A là \(C^3_{81}\left(cách\right)\)
Câu 2:
\(\overline{abc}\)
a có 9 cách
b có 9 cách
c có 8 cách
=>có 9*9*8=81*8=648(số)
Số cách chọn ngẫu nhiên 2 số từ tập A là \(C^2_{648}\left(cách\right)\)
Đúng 2
Bình luận (1)
`C1: n(A)=9.9=81`
`=>` Có `C_81 ^3 =85320` cách chọn `3` số ngẫu nhiên từ `A.`
`C2: n(A)=9.9.8=648`
`=>` Có `C_648 ^2 =209628` cách chọn `2` số ngẫu nhiên từ `A.`
Đúng 1
Bình luận (0)
-Viết các tập hợp sau bằng cách liệt kê các phần tử và cho biết số phần tử của mỗi tập hợp:
a. Tập hợp A các số tự nhiên có hai chữ số, trong đó chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2.
b. Tập hợp B các số tự nhiên có ba chữ số mà tổng các chữ số bằng 3.
a) \(A=\left\{20;31;42;53;64;75;86;97\right\}\)
b)\(B=\left\{102;120;111;201;210\right\}\)
Đúng 1
Bình luận (0)
a: A={31;42;53;64;75;86;97}
b: B={111;201;210;102;300}
Đúng 3
Bình luận (0)
Cho tập hợp P= {0;4;9}.Hãy viết các số tự nhiên :
a)Có ba chữ số và tập hợp các chữ số của nó là tập P.
b)Có ba chữ số lấy trong tập P.
Lời giải:
a) \(P=\left\{490; 409; 940; 904\right\}\)
b)
\(P=\left\{444; 440; 404; 409; 490; 499; 449; 494; 400; 999; 994; 990; 900; 904; 909;940; 949; 944\right\}\)
Đúng 8
Bình luận (1)
ai hướng dẫn cko mình chứ mình ko bt làm bài này
Đúng 0
Bình luận (0)
a) Vì số tự nhiên có ba chữ số và tập hợp các chữ số của nó là tập P nghĩa là số tự nhiên có ba chữ số khác nhau được tạo thành từ ba chữ số 0; 4; 9
Gọi số tự nhiên có ba chữ số khác nhau là 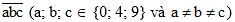
Vì chữ số hàng trăm khác 0 nên a = 4 hoặc a = 9.
+) Với a = 4, ta có các số thỏa mãn là: 409; 490
+) Với a = 9, ta có các số thỏa mãn là: 904; 940
Vậy ta được các số thỏa mãn đề bài là: 409; 490; 904; 940.
b) Vì số tự nhiên có ba chữ số lấy trong tập P thì các số cần tìm được viết bởi 0; 4; 9 nhưng không nhất thiết có mặt cả ba chữ số đó. Vậy mỗi chữ số có thể không có mặt hoặc có mặt 1; 2 hoặc 3 lần.
Gọi số tự nhiên có ba chữ số là 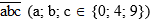
Vì chữ số hàng trăm khác 0 nên a = 4 hoặc a = 9
Trường hợp 1: a = 4
+) Với a = 4, b = 0 ta có ba số: 400; 404; 409
+) Với a = 4, b = 4 ta được ba số: 440; 444; 449
+) Với a = 4, b = 9 ta được ba số: 490; 494; 499
Trường hợp 2: Với a = 9
+) Với a = 9, b = 0 ta được ba số: 900; 904; 909
+) Với a = 9; b = 4 ta được ba số: 940; 944; 949
+) Với a = 9, b = 9 ta được ba số: 990; 994; 999
Vậy các số thỏa mãn điều kiện đề bài là: 400; 404; 409; 440; 444; 449; 490; 494; 499; 900; 904; 909; 940; 944; 949; 990; 994; 999
Đúng 0
Bình luận (0)


 B = {20; 50}
B = {20; 50}


