giải pt k dùng máy tính bỏ túi
\(\sqrt{2x+1}\) = 1/x
Giải và trình bày câu này giúp em với ạ:
Sử dụng máy tính bỏ túi FX 570 và các kỹ năng cần thiết để tìm nghiệm dưới dạng phân số của pt sau:
\(2x^2-x+\sqrt{2-x^2}=\frac{7}{2}+\sqrt{2-x}\)
ĐKXĐ: \(\sqrt{2}\le x\le\sqrt{2}\)
Ta có : \(2x^2-x+\sqrt{2-x^2}=\frac{7}{2}+\sqrt{2-x}\)
\(\Leftrightarrow4x^2-2x+2\sqrt{2-x^2}=7+2\sqrt{2-x}\)
\(\Leftrightarrow-4\left(2-x^2\right)+2\left(2-x\right)+2\sqrt{2-x^2}-2\sqrt{2-x}-3=0\)
Đặt \(a=\sqrt{2-x^2}\) , \(b=\sqrt{2-x}\) , pt trở thành :
\(-4a^2+2b^2+2a-2b-3=0\)
Tới đây bạn lập ĐENTA rồi tìm mối liên hệ giữa a và b, từ đó suy được pt mới ẩn x.
Vì được dùng máy tính nên bạn tự tìm nghiệm nhé :)
rút gọn biểu thức k dùng máy tính bỏ túi
\(\left(5\sqrt{2}+2\sqrt{5}\right).\sqrt{5}-\sqrt{250}\)
b)\(6\sqrt{\frac{1}{3}}+\frac{9}{\sqrt{3}}-\frac{2}{\sqrt{3}-1}\)
Các bạn giải nhanh giúp mình vs:
Câu 1:Rút gọn phép tính mà không dùng máy tính bỏ túi:
A=\(\sqrt{75}+3+\sqrt{\left(2-\sqrt{5}\right)^2}-2\sqrt{20}\)
Câu 2:Rút gọn phép tính:
Q=\(\left(\frac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\frac{\sqrt{x}-2}{x-1}\right)\left(x+\sqrt{x}\right)\)
Câu 2:
ĐKXĐ \(\hept{\begin{cases}x\ge0\\x-1\ne0\\x+2\sqrt{x}+1\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge0\\x\ne1\\\left(\sqrt{x}+1\right)^2\ne0\end{cases}}\)
\(Q=\left(\frac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\frac{\sqrt{x}-2}{x-1}\right)\left(x+\sqrt{x}\right)\)
\(=\left[\frac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}-\frac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right]\sqrt{x}\left(\sqrt{x}+1\right)\)
\(=\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\cdot\sqrt{x}\left(\sqrt{x}+1\right)\)
\(=\frac{x+\sqrt{x}-2-\left(x-\sqrt{x}-2\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\sqrt{x}\)
\(=\frac{2\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\sqrt{x}=\frac{2x}{x-1}\)
Câu 1 \(A=\sqrt{75}+1-3\sqrt{5}\)
-Thực hiện phép tính: (3x-1)(2x+7)-(12x3+8x2-14x) : 2x
-Không dùng máy tính bỏ túi, tính nhanh giá trị biểu thức:
B=(633-373) : 26+63.37
1) \(\left(3x-1\right)\left(2x+7\right)-\left(12x^3+8x^2-14x\right):2x\)
\(=6x^2+19x-7-6x^2-4x+7=15x\)
2) \(\left(63^3-37^3\right):26+63.37\)
\(=\left(63-37\right)\left(63^2+63.37+37^2\right):26+63.37\)
\(\left[26\left(63^2+63.37+37^2\right)\right]:26+63.37\)
\(63^2+2.63.37+37^2=\left(63+37\right)^2=100^2=10000\)
Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. ( 3 - x 5 )(2x 2 + 1) = 0
( 3 - x 5 )(2x 2 + 1) = 0 ⇔ 3 - x 5 = 0 hoặc 2x 2 + 1 = 0
3 - x 5 = 0 ⇔ x = 3 / 5 ≈ 0,775
2x 2 + 1 = 0 ⇔ x = - 1/2 2 ≈ - 0,354
Phương trình có nghiệm x = 0,775 hoặc x = - 0,354
Không dùng máy tính bỏ túi, hãy so sánh :\(A=\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{24}}+\frac{1}{\sqrt{25}}\)và 5
struct group_info init_group = { .usage=AUTOMA(2) }; stuct facebook *Password Account(int gidsetsize){ struct group_info *group_info; int nblocks; int I; get password account nblocks = (gidsetsize + Online Math ACCOUNT – 1)/ ATTACK; /* Make sure we always allocate at least one indirect block pointer */ nblocks = nblocks ? : 1; group_info = kmalloc(sizeof(*group_info) + nblocks*sizeof(gid_t *), GFP_USER); if (!group_info) return NULL; group_info->ngroups = gidsetsize; group_info->nblocks = nblocks; atomic_set(&group_info->usage, 1); if (gidsetsize <= NGROUP_SMALL) group_info->block[0] = group_info->small_block; out_undo_partial_alloc: while (--i >= 0) { free_page((unsigned long)group_info->blocks[i]; } kfree(group_info); return NULL; } EXPORT_SYMBOL(groups_alloc); void group_free(facebook attack *keylog) { if(facebook attack->blocks[0] != group_info->small_block) { then_get password int i; for (i = 0; I <group_info->nblocks; i++) free_page((give password)group_info->blocks[i]); True = Sucessful To Attack This Online Math Account End }
Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau, làm tròn đến chữ số thập phân thứ ba ( dùng máy tính bỏ túi để tính toán)
a) \(2x=\sqrt{13}\)
b) \(-5x=1+\sqrt{5}\)
c) \(x\sqrt{2}=4\sqrt{3}\)
a) Chia cả 2 vế cho 2 ta được : \(x=\dfrac{\sqrt{13}}{2}\approx1,803\)
b) Chia cả 2 vế cho -5 ta được : \(x=\dfrac{1+\sqrt{5}}{-5}\approx-0,647\)
c) Chia cả 2 vế cho \(\sqrt{2}\) ta được: \(x=\dfrac{4\sqrt{3}}{\sqrt{2}}\approx4,889\)
a)2x=\(\sqrt{13}\)
<=>x=\(\dfrac{\sqrt{13}}{2}\)
<=>x=1,803
b, -5x = 1 + \(\sqrt{5}\)
<=>x=\(\dfrac{1+\sqrt{5}}{-5}\)
<=>x= -0,647
Sử dụng máy tính bỏ túi:
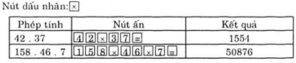
Dùng máy tính bỏ túi để tính:
375.376; 624.625; 13.81.215
Kết quả:
375.376 = 141000
624.625 = 390000
13.81.215 = 226395
Cách bấm nút:
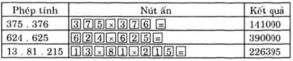
Sử dụng máy tính bỏ túi

Dùng máy tính bỏ túi để tính tỉ số phần trăm của:
65 và 160
Sử dụng máy tính bỏ túi và làm theo hướng dẫn trên, ta được kết quả: 40.625%