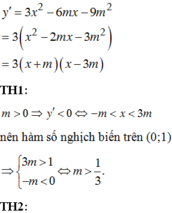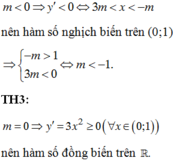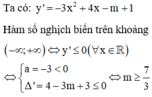Tìm tất cả các giá trị thực của tham số m để hàm số y=x3-3mx2-9m2x nghịch biến trên khoảng (0;1)
DT
Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
-
9
m
2
x
nghịch biến trên khoảng (0;1) A.
m
≥...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 - 9 m 2 x nghịch biến trên khoảng (0;1)
A. m ≥ 1 3 hoặc m ≤ - 1
B. m > 1 3
C. m < - 1
D. - 1 < m < 1 3
Đáp án A
Phương pháp: Để hàm số nghịch biến trên ![]() và y’ = 0 tại hữu hạn điểm.
và y’ = 0 tại hữu hạn điểm.
Cách giải: TXĐ: D =R
![]()
![]()
![]()
![]()
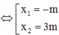
![]() nằm trong khoảng 2 nghiệm x1; x2
nằm trong khoảng 2 nghiệm x1; x2
Hàm số nghịch biến trên khoảng (0;1) khi và chỉ khi:
TH1: 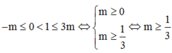
TH2: 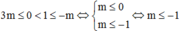
Vậy m ≥ 1 3 hoặc m ≤ - 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số thực m để hàm số
y
x
3
−
3
m
x
2
−
9
m
2
x
nghịch biến trên
0
;
1
.
A.
m
1
3
.
B.
m
−
1....
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để hàm số y = x 3 − 3 m x 2 − 9 m 2 x nghịch biến trên 0 ; 1 .
A. m > 1 3 .
B. m < − 1.
C. m > 1 3 h o ặ c m < − 1.
D. − 1 < m < 1 3 .
Đáp án C.
Ta có:
y ' = 3 x 2 − 6 m x − 9 m 2 = 3 x 2 − 2 m x − 3 m 2 = 3 x + m x − 3 m
TH1: Nếu m > 0 ⇒ y ' < 0 ⇔ − m < x < 3 m nên hàm số nghịch biến trên 0 ; 1 ⇒ 3 m > 1 − m < 0 ⇔ m > 1 3 .
TH2: Nếu m < 0 ⇒ y ' < 0 ⇔ 3 m < x < − m nên hàm số nghịch biến trên 0 ; 1 ⇒ − m > 1 3 m < 0 ⇔ m < − 1.
TH3: Nếu m = 0 ⇒ y ' = 3 x 2 ≥ 0 ∀ x ∈ 0 ; 1 nên hàm số đồng biến trên ℝ
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số thực m để hàm số
y
x
3
-
3
m
x
2
-
9
m
x
nghịch biến trên (0;1). A. m 1/3 B. m -1 C. m 1/3 hoặc m -1 D. -1 m 1/3
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để hàm số y = x 3 - 3 m x 2 - 9 m x nghịch biến trên (0;1).
A. m > 1/3
B. m < -1
C. m > 1/3 hoặc m < -1
D. -1< m <1/3
Tìm tất cả các giá trị thực của tham số m để hàm số
f
x
1
π
x
3
−
3
m
x
2
+
m
nghịch biến trên khoảng
−
∞
;...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số f x = 1 π x 3 − 3 m x 2 + m nghịch biến trên khoảng − ∞ ; + ∞
A. m ∈ 0 ; + ∞
B. m = 0
C. m ≠ 0
D. m ∈ ℝ
Đáp án B
Xét hàm số f x = 1 π x 3 − 3 m x 2 + m , ta có f ' x = 3 x 2 − 6 m x . 1 π x 3 − 3 m x 2 + m . ln 1 π .
Để hàm số đã cho nghịch biến trên khoảng
− ∞ ; + ∞ ⇔ f ' x ≤ 0 ; ∀ x ∈ ℝ ⇔ 3 x 2 − 6 m x ≥ 0 ; ∀ x ∈ ℝ
⇔ x x − 2 m ≥ 0 ; ∀ x ∈ ℝ ⇒ m = 0 là giá trị cần tìm.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
f
x
3
π
x
3
-
3
m
x
2
+
m
nghịch biến trên khoảng
-
∞
;...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số f x = 3 π x 3 - 3 m x 2 + m nghịch biến trên khoảng - ∞ ; + ∞
A . m ≠ 0
B . m = 0
C . m ∈ ( 0 ; + ∞ )
D . m ∈ R
Tìm tất cả các giá trị thực của tham số m để hàm số
f
x
1
π
x
3
-
3
m
x
2
+
m
nghịch biến trên khoảng
-
∞
;...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số f x = 1 π x 3 - 3 m x 2 + m nghịch biến trên khoảng - ∞ ; + ∞ ?
A. m ∈ 0 ; + ∞
B. m = 0
C. m ≠ 0
D. m ∈ ℝ
Đáp án B
Xét hàm số f x = 1 π x 3 - 3 m x 2 + m , ta có
f ' x = 3 x 2 - 6 m x . 1 π x 3 - 3 m x 2 + m . ln 1 π .
Để hàm số đã cho nghịch biến trên khoảng - ∞ ; + ∞
⇔ f ' x ≤ 0 ; ∀ x ∈ ℝ ⇔ 3 x 2 - 6 m x ≥ 0 ; ∀ x ∈ ℝ
⇔ x x - 2 m ≥ 0 ; ∀ x ∈ ℝ ⇒ m = 0 .
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
f
x
3
π
x
3
-
3
m
x
2
+
m
nghịch biến trên khoảng
-
∞
;...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số f x = 3 π x 3 - 3 m x 2 + m nghịch biến trên khoảng - ∞ ; + ∞
A . m ≠ 0
B . m = 0
C . m ∈ ( 0 ; + ∞ )
D . m ∈ R
Tìm tất cả các giá trị thực của tham số m để hàm số
y
-
x
3
+
2
x
2
-
m
-
1
x
+
2
nghịch biến trên khoảng
-
∞
;
+
∞
A.
m
≤
7...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 2 x 2 - m - 1 x + 2 nghịch biến trên khoảng - ∞ ; + ∞
A. m ≤ 7 3
B. m ≥ 7 3
C. m ≥ 1 3
D. m > 7 3
Tìm tất cả các giá trị thực của tham số m để hàm số
y
-
x
3
+
2
x
2
-
(
m
-
1
)
x
+
2
nghịch biến trên khoảng (-∞;+∞) A.
m
≤
7
3
B.
m
≥
7
3
C....
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 2 x 2 - ( m - 1 ) x + 2 nghịch biến trên khoảng (-∞;+∞)
A. m ≤ 7 3
B. m ≥ 7 3
C. m ≥ 1 3
D. m > 7 3
Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
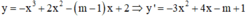
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞)
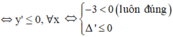
![]()
![]()
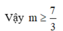
Đúng 0
Bình luận (0)