ChọnB

a: Xét ΔABC có 

M là trung điểm của AB

N là trung điểm của BC

Do đó: MN là đường trung bình của ΔABC

Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)

\(\Leftrightarrow MN=\dfrac{12}{2}=6\left(cm\right)\)

b: Ta có: MN//AC và \(MN=\dfrac{AC}{2}\)

mà P\(\in\)AC và \(AP=\dfrac{AC}{2}\)(P là trung điểm của AC

nên MN//AP và MN=AP

Xét ΔABC có 

M là trung điểm của AB

P là trung điểm của AC

Do đó: MP là đường trung bình của ΔABC

Suy ra: MP//BC và \(MP=\dfrac{BC}{2}\)

mà N\(\in\)BC và \(BM=\dfrac{BC}{2}\)

nên MP//BN và MP=BN

Xét tứ giác AMNP có 

MN//AP

MN=AP

Do đó: AMNP là hình bình hành

Xét tứ giác BMPN có 

MP//BN

MP=BN

Do đó: BMPN là hình bình hành

c) Hình bình hành AMNP trở thành hình vuông khi \(\left\{{}\begin{matrix}\widehat{MAP}=90^0\\AM=AP\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{BAC}=90^0\\AB=AC\end{matrix}\right.\)

a:BC=20cm

MN=10cm

* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.

Suy ra: DE// BC và

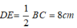
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.

Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D

a) Xét tam giác ABC có:

M là trung điểm AB(gt)

N là trung điểm BC(gt)

=> MN là đường trung bình

=> MN//AC

Mà AC⊥AB(tam giác ABC vuông tại A)

=> MN⊥AB(từ vuông góc đến song song)

b) Xét tam giác ABC vuông tại A:

\(BC^2=AB^2+AC^2\left(pytago\right)\)

\(\Rightarrow AC^2=BC^2-AB^2=13^2-12^2=25\Rightarrow AC=5\left(cm\right)\)

Ta có: MN là đường trung bình tam giác ABC

\(\Rightarrow MN=\dfrac{1}{2}AC=\dfrac{1}{2}.5=2,5\left(cm\right)\)

D và E là trung điểm của AB và AC => DE là đường trung bình của tam giác ABC

=> DE//BC và DE=1/2 BC = 9cm

Tứ giác DECB có DE // BC => Hình thang DECB đáy DE, CB

Lại có M, N là trung điểm BD và CE=> MN là đường trung bình của hình thang DECB

=> MN = 1/2 ( DE + BC) = 1/2 (9+18) = 13,5 (cm)

Vậy....................................

________________________JK~ Liên Quân Group ________________________

a, Ta có:\(AB^2+AC^2=12^2+16^2=400\)(cm)

\(BC^2=20^2=400\)(cm)

\(\Rightarrow AB^2+AC^2=BC^2\)

\(\Rightarrow\Delta ABC\) vuông tại A

Xét Δ DNC và Δ ABC có:

\(\widehat{NDC}=\widehat{BAC}\left(=90^o\right)\)

Chung \(\widehat{C}\)

⇒Δ DNC \(\sim\) Δ ABC (g.g)

b, Ta có: BD=DC=1/2.BC=1/2.20=10(cm)

Δ DNC \(\sim\) Δ ABC (cma)

\(\Rightarrow\dfrac{ND}{AB}=\dfrac{NC}{BC}=\dfrac{DC}{AC}\Rightarrow\dfrac{ND}{12}=\dfrac{NC}{20}=\dfrac{10}{16}\Rightarrow\left\{{}\begin{matrix}ND=7,5\left(cm\right)\\NC=12,5\left(cm\right)\end{matrix}\right.\)

c, Xét Δ DBM và Δ ABC có:

Chung \(\widehat{B}\)

\(\widehat{BDM}=\widehat{BAC}\left(=90^o\right)\)

⇒Δ DBM \(\sim\) Δ ABC(g.g)

\(\Rightarrow\dfrac{MB}{BC}=\dfrac{BD}{AB}\Rightarrow\dfrac{MB}{20}=\dfrac{10}{12}\Rightarrow MB=\dfrac{50}{3}\left(cm\right)\)

Ta có: MD⊥BC, BD=DC ⇒ ΔBDC cân tại M

\(\Rightarrow MB=MC=\dfrac{50}{3}\left(cm\right)\)