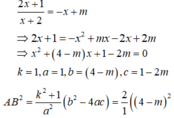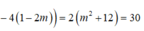cho hàm số y=x2-3x+2. Xét (d): y=x+m. tìm m để (d) cắt (p) tại 2 điểm phân biệt
NN
Những câu hỏi liên quan
Cho hàm số y=x2 có đồ thị (P) Tìm m để đường thẳng (d'):y=x-2m+1 cắt (P) tại 2 điểm phân biệt
Phương trình hoành độ giao điểm:
\(x^2=x-2m+1\)
\(\Leftrightarrow x^2-x+2m-1=0\)
Yêu cầu bài toán thỏa mãn khi phương trình \(x^2-x+2m-1=0\) có hai nghiệm phân biệt
\(\Leftrightarrow\Delta=1-8m+4=5-8m>0\)
\(\Leftrightarrow m< \dfrac{5}{8}\)
Đúng 1
Bình luận (0)
Phương trình hoành độ giao điểm là:
\(x^2-x+2m-1=0\)
\(\text{Δ}=1^2-4\cdot1\cdot\left(2m-1\right)\)
\(=1-8m+4\)
\(=-8m+5\)
Để \(\left(P\right),\left(d'\right)\) cắt nhau tại hai điểm phân biệt thì -8m+5>0
hay \(m< \dfrac{5}{8}\)
Đúng 0
Bình luận (0)
a) lập bảng biến thiên và vẽ đồ thị hàm số y = x\(^2\)+3x+2
b) tìm m để đường thẳng y = -x+m cắt (P) tại 2 điểm phân biệt có hoành độ dương
c) tìm m để đường thẳng y = -2x+3m cắt (P) tại 2 điểm phân biệt có hoành độ x1, x2 thỏa mãn x\(_1\)= 3x\(_2\)
Cho hai hàm số : (P) y = \(x^2\) và (d) y = 2mx + 2m +1 với m là tham số
Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ x1,x2 sao cho
\(\sqrt{x1+x2}\) + \(\sqrt{3+x1.x2}\) = 2m + 1
Lời giải:
PT hoành độ giao điểm:
$x^2-2mx-(2m+1)=0(*)$
Để (P) và (d) cắt nhau tại 2 điểm pb có hoành độ $x_1,x_2$ thì PT $(*)$ phải có 2 nghiệm pb $x_1,x_2$
$\Leftrightarrow \Delta'=m^2+2m+1>0\Leftrightarrow (m+1)^2>0$
$\Leftrightarrow m\neq -1$
Áp dụng định lý Viet: $x_1+x_2=2m; x_1x_2=-(2m+1)$
Khi đó:
$\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1$
$\Leftrightarrow \sqrt{2m}+\sqrt{3-2m-1}=2m+1$
\(\Leftrightarrow \left\{\begin{matrix}
0\leq m< 1\\
\sqrt{2m}+\sqrt{2(1-m)}=2m+1\end{matrix}\right.\)
Bình phương 2 vế dễ dàng giải ra $m=\frac{1}{2}$ (thỏa)
Đúng 2
Bình luận (0)
Cho (P) y=\(x^2\) và (d) y= 3x + \(m^2\)-2
a) Chứng minh: (d) luôn cắt (P) tại hai điểm phân biệt
b) Gọi x1 và x2 là hoành độ giao điểm của (d) và (P) .Tìm m để |x1| + 2|x2|= 3
a, Xét hoành độ giao điểm của P và d ta có:
x2 = 3x + m2 - 2
\(\Delta=b^2-4ac=4m^2+1>0\) ∀x
=> d luôn cắt P tại hai điểm phân biệt.
Đúng 0
Bình luận (0)
Bài 1: Cho hàm số y= -x2 (P) và y = 2x + m - 3 (d)
Tìm đk để tham số m để đt (d) cắt (P) tại 2 điểm phân biệt M (x1,x2); N (x1,x2) thỏa mãn: ( y1 + 2x2 + m ).(y2 + 2x1 - 3m) = -51
(mink đag cần gấp)
Cho (d): y = 3x - m + 4 và (P): y = x2
Tìm m để (d) cắt (P) tại 2 điểm phân biệt sao cho x12 + 3x2 - 4x1x2 = 5
Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=3x-m+4\)
\(\Leftrightarrow x^2-3x+m-4=0\)
a=1; b=-3; c=m-4
\(\Delta=b^2-4ac=\left(-3\right)^2-4\cdot1\cdot\left(m-4\right)\)
\(\Leftrightarrow\Delta=9-4m+16=-4m+25\)
Để (d) cắt (P) tại hai điểm phân biệt thì phương trình hoành độ giao điểm của (P) và (d) có hai nghiệm phân biệt
hay Δ>0
\(\Leftrightarrow-4m+25>0\)
\(\Leftrightarrow-4m>-25\)
hay \(m< \dfrac{25}{4}\)
Khi \(m< \dfrac{25}{4}\), Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=3\\x_1\cdot x_2=m-4\end{matrix}\right.\)
Ta có: \(x_1^2+3x_2-4x_1x_2=5\)
\(\Leftrightarrow x_1^2+x_2\left(x_1+x_2\right)-4x_1x_2=5\)
\(\Leftrightarrow x_1^2+x_1\cdot x_2+x_2^2-4x_1x_2=5\)
\(\Leftrightarrow x_1^2+x_2^2-3x_1x_2=5\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-5x_1x_2=5\)
\(\Leftrightarrow3^2-5\left(m-4\right)=5\)
\(\Leftrightarrow9-5m+20-5=0\)
\(\Leftrightarrow-5m=-24\)
hay \(m=\dfrac{24}{5}\)(thỏa ĐK)
Vậy: \(m=\dfrac{24}{5}\)
Đúng 2
Bình luận (0)
Cho hàm số
y
x
2
−
2
x
−
2
có đồ thị (P), và đường thẳng (d) có phương trình
y
x
+
m
. Tìm m để (d) cắt (P) tại hai điểm phân biệt A, B sao cho
O
A
2
+
O
B
2
đạt giá trị nhỏ nhất A.
m
−
5...
Đọc tiếp
Cho hàm số y = x 2 − 2 x − 2 có đồ thị (P), và đường thẳng (d) có phương trình y = x + m . Tìm m để (d) cắt (P) tại hai điểm phân biệt A, B sao cho O A 2 + O B 2 đạt giá trị nhỏ nhất
A. m = − 5 2
B. m = 5 2
C. m = 1
D. m = 2
Phương trình hoành độ giao điểm: x 2 − 2 x − 2 = x + m ⇔ x 2 − 3 x − 2 − m = 0
(d) cắt (P) tại hai điểm phân biệt A, B ⇔ Δ > 0 ⇔ 17 + 4 m > 0 ⇔ m > − 17 4
Giả sử (*) có hai nghiệm x 1 , x 2 thì x 1 + x 2 = − b a = 3 x 1 . x 2 = c a = − m − 2
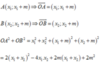
= 18 − 4 ( − 2 − m ) + 6 m + 2 m 2 = 2 m 2 + 10 m + 26 = 2 m + 5 2 2 + 27 2 ≥ 27 2 với m > − 17 4
Vậy giá trị nhỏ nhất của O A 2 + O B 2 là 27 2 khi m = − 5 2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
1) cho hàm số y=2x+b. Tìm b để hàm số cắt trục hoành tại điểm có hoành độ bằng 3.
2) Cho Parabol (P): y=x2 và đường thẳng d: y=(m-1)x+m-4. Tìm m để d cắt (P) tại 2 điểm phân biệt nằm về 2 phía của trục tung.
1, Do hàm số trên cắt trục hoành tại điểm có hoành độ bằng 3 hay hàm số trên đi qua A(3;0)
<=> \(0=6+b\Leftrightarrow b=-6\)
2, Hoành độ giao điểm (P) ; (d) tm pt
\(x^2-\left(m-1\right)x-m+4=0\)
Để (P) cắt (d) tại 2 điểm pb nằm về 2 phía trục tung khi pt có 2 nghiệm trái dấu hay
\(x_1x_2=-m+4< 0\Leftrightarrow-m< -4\Leftrightarrow m>4\)
Cho hàm số
y
2
x
+
1
x
+
2
(C);
y
-
x
+
m
(d) Tìm m để (C) luôn cắt (d) tại 2 điểm phân biệt A, B sao cho
A
B
30
A.
m
±
3
B.
m
±...
Đọc tiếp
Cho hàm số y = 2 x + 1 x + 2 (C); y = - x + m (d) Tìm m để (C) luôn cắt (d) tại 2 điểm phân biệt A, B sao cho A B = 30
A. m = ± 3
B. m = ± 3
C. m = ± 2
D. m = ± 2
Cho hàm số y= X/X-1 . tìm m để đt (d) y= -X+m cắt đồ thị tại 2 điểm phân biệt.