`P=n^3-n^2+n-1`

`=n^2(n-1)+(n-1)`

`=(n-1)(n^2+1)`

Vì n là stn thì p là snt khi

`n-1=1=>n=2`

Vậy n=2

Ta có :

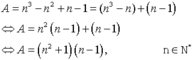
Nếu n = 1 suy ra A = 0

Nếu n = 2 suy ra A = 5 là số nguyên tố

Nếu n>2 thì A là tích của hai thừa số mà mỗi thừa số đều lớn hơn hai . Vậy A là hợp số

Vậy để A = n³ – n² + n – 1 là số nguyên tố thì n = 2.

1,

Đặt A = n3 - n2 + n - 1

Ta có A = n2(n - 1) + (n - 1) = (n - 1)(n2 + 1)

Vì A nguyên tố nên A chỉ có 2 Ư. Ư thứ 1 là 1 còn Ư thứ 2 nguyên tố nên ta suy ra 2 trường hợp :

TH1 : n - 1 = 1 và n2 + 1 nguyên tố 
⇒
n = 2 và n2 + 1 = 5 nguyên tố (thỏa)

TH2 : n2 + 1 = 1 và n - 1 nguyên tố 
⇒
n = 0 và n - 1 = - 1( ko thỏa)

Vậy n = 2

2 , 

Xột số   A = (2n – 1)2n(2n + 1)

A là tích của 3 số tự nhiên liờn tiệp nên A   ⋮   3  

Mặt khỏc 2n – 1 là số nguyên tố   ( theo giả thiết )

                2n  không chia hết cho 3

Vậy 2n + 1 phải chia hết cho 3 ⇒  2n + 1 là hợp số.

3 , 

Giải:

Với m=2 thì m2+2=4+2= 6 là hợp số (loại)

Với m=3 thì m2+2 = 9+2= 11 (thoải mãn)

Với m= 3k+1 ( với k ẻ N) thì: m2+2 = (3k+1)2 +2 = 3(3k2+2k+1) là hợp số ( loại)

Với m= 3k+2 thì: m2+2= (3k+2)2 +2 = 3(3k2+4k+2) là hợp số (loại)

Vậy với m= 3 thì m và m2+2 là số nguyên tố. Khi đó m3+ 2= 33+2 = 29 là số nguyên tố.

\(P=\dfrac{n^3+3n^2+2n}{6}+\dfrac{2n+1}{1-2n}\)

Vì n^3+3n^2+2n=n(n+1)(n+2) là tích của 3 số liên tiếp

nên n^3+3n^2+2n chia hết cho 3!=6

=>Để P nguyên thì 2n+1/1-2n nguyên

=>2n+1 chia hết cho 1-2n

=>2n+1 chia hết cho 2n-1

=>2n-1+2 chia hết cho 2n-1

=>\(2n-1\in\left\{1;-1;2;-2\right\}\)

=>\(n\in\left\{1;0;\dfrac{3}{2};-\dfrac{1}{2}\right\}\)

\(2,\\ n=0\Leftrightarrow A=1\left(loại\right)\\ n=1\Leftrightarrow A=3\left(nhận\right)\\ n>1\Leftrightarrow A=n^{2012}-n^2+n^{2002}-n+n^2+n+1\\ \Leftrightarrow A=n^2\left[\left(n^3\right)^{670}-1\right]+n\left[\left(n^3\right)^{667}-1\right]+\left(n^2+n+1\right)\)

Ta có \(\left(n^3\right)^{670}-1⋮\left(n^3-1\right)=\left(n-1\right)\left(n^2+n+1\right)⋮\left(n^2+n+1\right)\)

Tương tự \(\left(n^3\right)^{667}⋮\left(n^2+n+1\right)\)

\(\Leftrightarrow A⋮\left(n^2+n+1\right);A>1\)

Vậy A là hợp số với \(n>1\)

Vậy \(n=1\)

\(3,\)

Đặt \(A=n^4+n^3+1\)

\(n=1\Leftrightarrow A=3\left(loại\right)\\ n\ge2\Leftrightarrow\left(2n^2+n-1\right)^2\le4A\le\left(2n^2+n\right)^2\\ \Leftrightarrow4A=\left(2n^2+n\right)^2\\ \Leftrightarrow4n^2+4n^3+4=4n^2+4n^3+n^2\\ \Leftrightarrow n^2=4\Leftrightarrow n=2\)

Vậy \(n=2\)

n = 3.

Để \(\left(n-1\right)\left(n^2+2n+3\right)\) là số nguyên tố <=> \(n-1=1\) hoặc \(n^2+2n+3=1\)

TH1 : \(n-1=1\Rightarrow n=2\)

\(\Rightarrow\left(n-1\right)\left(n^2+2n+3\right)=\left(2-1\right)\left(2^2+2.2+3\right)=11\)là số nguyên tố (TM)

TH2 : \(n^2+2n+3=1\)

\(\Leftrightarrow\left(n^2+2n+1\right)+2=1\Leftrightarrow\left(n+1\right)^2+2=1\Rightarrow\left(n+1\right)^2=-1\) (loại vì \(\left(n+1\right)^2\ge0\) )

Vậy n = 2 thì \(\left(n-1\right)\left(n^2+2n+3\right)\)là số nguyên tố 

ta có (n+3)(n+1) là số nguyên tố \(\Leftrightarrow\orbr{\begin{cases}n+3=1\\n+1=1\end{cases}\Leftrightarrow\orbr{\begin{cases}n=1-3\\n=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}n=-2\\n=0\end{cases}}}\)

                                                                                                                                Mà \(n\in N\)

\(\Rightarrow\)n=0