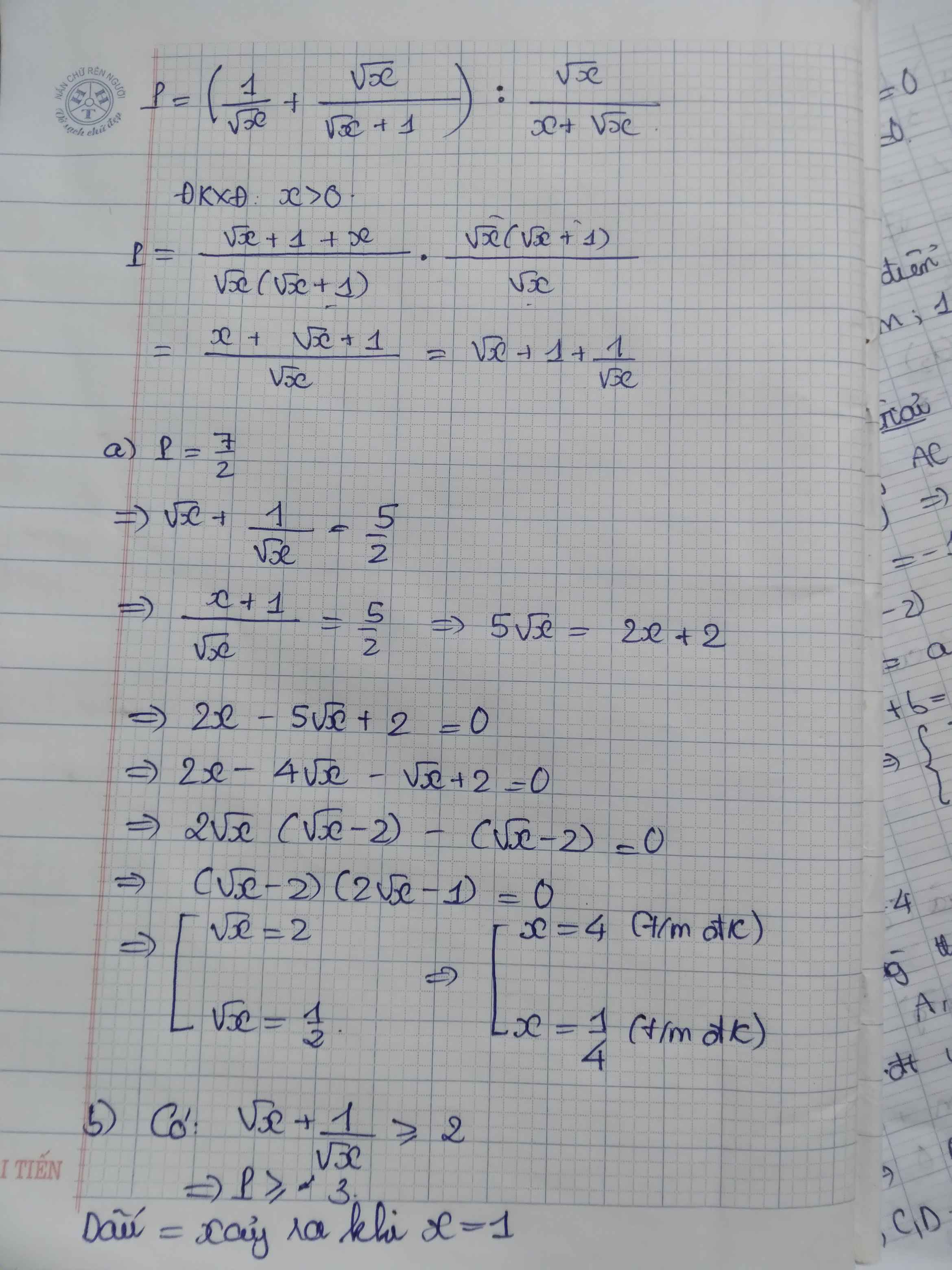Tìm giá trị lớn nhất của P=\(\dfrac{\sqrt{x}-1}{\sqrt{x}}\)\(-16\sqrt{x}\) HELP ME!!!!
TP
Những câu hỏi liên quan
Cho \(A=\dfrac{2+\sqrt{x}}{\sqrt{x}}\)
\(B=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
Tìm x nguyên lớn nhất để \(\dfrac{A}{B}>\dfrac{3}{2}\)
Help me plssssss
\(P=A:B=\dfrac{\sqrt{x}+2}{\sqrt{x}}:\dfrac{\sqrt{x}+2}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
P>3/2
=>P-3/2>0
=>\(\dfrac{\sqrt{x}+1}{\sqrt{x}}-\dfrac{3}{2}>0\)
=>\(\dfrac{2\sqrt{x}+2-3\sqrt{x}}{2\sqrt{x}}>0\)
=>-căn x+2>0
=>-căn x>-2
=>0<x<4
Đúng 0
Bình luận (0)
P=\(\dfrac{3\left(x+\sqrt{x}-3\right)}{x+\sqrt{x}-2}+\dfrac{\sqrt{x}+3}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
a) RG P b)Tìm giá trị lớn nhất của P
a.\(P=\dfrac{3\left(x+\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}+2}-\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
\(ĐK:x\ge0;x\ne1;x\ne-2\)
\(P=\dfrac{3x+3\sqrt{x}-9}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}+\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(P=\dfrac{3x+3\sqrt{x}-9+x-\sqrt{x}+3\sqrt{x}-3-x+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(P=\dfrac{3x+5\sqrt{x}-8}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(P=\dfrac{\left(\sqrt{x}-1\right)\left(3\sqrt{x}+8\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(P=\dfrac{3\sqrt{x}+8}{\sqrt{x}+2}\)
b.\(P=\dfrac{3\sqrt{x}+8}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2}{\sqrt{x}+2}+\dfrac{\sqrt{x}+2}{\sqrt{x}+2}+\dfrac{\sqrt{x}+2}{\sqrt{x}+2}+\dfrac{2}{\sqrt{x}+2}\)
\(=1+1+1+\dfrac{2}{\sqrt{x}+2}\)
Để P lớn nhất thì \(\sqrt{x}+2\) nhỏ nhất
Mà \(\sqrt{x}+2\ge2\) \(\Rightarrow Min=2\)
\(\Rightarrow P\le1+1+1+\dfrac{2}{2}=1+1+1+1=4\)
Vậy \(P_{max}=4\) khi \(x=0\)
Đúng 1
Bình luận (1)
\(P=\dfrac{1}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+1}+\dfrac{2\sqrt{x}-7}{x-\sqrt{x}-2} \) với x\(\ge\)0;x\(\ne\)44
a) CM \(P=\dfrac{1}{\sqrt{x}-2}
\)
b) tìm giá trị lớn nhất của P
a: \(P=\dfrac{\sqrt{x}+1-2\sqrt{x}+4+2\sqrt{x}-7}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}=\dfrac{1}{\sqrt{x}+1}\)
b: căn x+1>=1
=>P<=1
Dấu = xảy ra khi x=0
Đúng 1
Bình luận (0)
P=\(\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
1. Tìm giá trị của x để P=\(\dfrac{7}{2}\)
2. Tìm giá trị nhỏ nhất của P
1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
Để \(P=\dfrac{7}{2}\) thì \(2x+2\sqrt{x}+2-7\sqrt{x}=0\)
\(\Leftrightarrow2x-4\sqrt{x}-\sqrt{x}+2=0\)
\(\Leftrightarrow2\sqrt{x}\left(\sqrt{x}-2\right)-\left(\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
A=\(\left(\dfrac{2}{\sqrt{x}-3}+\dfrac{1}{\sqrt{x}+3}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) ,B=\(\dfrac{2\sqrt[]{x}+1}{\sqrt{x}+3}\)
với x\(\ge\)0,x\(\ne\)9
a)rút gọn A
b)tìm giá trị lớn nhất của A
c)với các biểu hức A,B nói trên,hãy tìm các giá trị nguyên của x để A:(B-1)là số nguyên
a: \(A=\dfrac{2\sqrt{x}+6+\sqrt{x}-3}{x-9}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{3\left(\sqrt{x}+1\right)}{x-9}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{3}{\sqrt{x}+3}\)
b: \(\sqrt{x}+3>=3\)
=>A<=1
Dấu = xảy ra khi x=0
c: \(P=A:\left(B-1\right)=\dfrac{3}{\sqrt{x}+3}:\dfrac{2\sqrt{x}+1-\sqrt{x}-3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{x}-2}\)
Để P nguyên thì căn x-2\(\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{1;25\right\}\)
Đúng 0
Bình luận (0)
cho biểu thức: P = \(\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\dfrac{\left(1-x\right)^2}{2}\)
a, Rút gọn P
b, Tìm giá trị của P khi x = 7 - \(4\sqrt{3}\)
c, Tìm x để P có giá trị lớn nhất
Tìm giá trị lớn nhất của A= \(\dfrac{\sqrt{z-1}}{z}+\dfrac{\sqrt{x-2}}{x}+\dfrac{\sqrt{y-3}}{y}\)
đkxđ: \(z\ge1;x\ge2;y\ge3\)
Đặt \(a=\sqrt{z-1}\ge0;b=\sqrt{x-2}\ge0;c=\sqrt{y-3}\ge0\)
\(\Rightarrow z=a^2+1;x=b^2+2;y=c^2+3\)
\(\Rightarrow A=\dfrac{a}{a^2+1}+\dfrac{b}{b^2+2}+\dfrac{c}{c^2+3}\)
Do các biến \(a,b,c\) độc lập nhau nên ta xét từng phân thức một.
Đặt \(f\left(a\right)=\dfrac{a}{a^2+1}\) \(\Rightarrow f\left(a\right).a^2-a+f\left(a\right)=0\) (*)
Nếu \(f\left(a\right)=0\) thì \(a=0\), rõ ràng đây không phải là GTLN cần tìm.
Xét \(f\left(a\right)\ne0\)
Để pt (*) có nghiệm thì \(\Delta=\left(-1\right)^2-4\left[f\left(a\right)\right]^2\ge0\)
\(\Leftrightarrow\left(1+2f\left(a\right)\right)\left(1-2f\left(a\right)\right)\ge0\)
\(\Leftrightarrow-\dfrac{1}{2}\le f\left(a\right)\le\dfrac{1}{2}\)
\(f\left(a\right)=\dfrac{1}{2}\Leftrightarrow\dfrac{a}{a^2+1}=\dfrac{1}{2}\Leftrightarrow a^2+1=2a\Leftrightarrow a=1\) (nhận)
Vậy \(max_{f\left(a\right)}=\dfrac{1}{2}\).
Tiếp đến, gọi \(g\left(b\right)=\dfrac{b}{b^2+2}\) \(\Rightarrow g\left(b\right).b^2-b+2g\left(b\right)=0\) (**)
Tương tự nếu \(b=0\) thì vô lí. Xét \(b\ne0\). Khi đó để (**) có nghiệm thì \(\Delta=\left(-1\right)^2-8\left[g\left(b\right)\right]^2\ge0\)
\(\Leftrightarrow\left(1-2\sqrt{2}g\left(b\right)\right)\left(1+2\sqrt{2}g\left(b\right)\right)\ge0\)
\(\Leftrightarrow-\dfrac{1}{2\sqrt{2}}\le g\left(b\right)\le\dfrac{1}{2\sqrt{2}}\)
\(g\left(b\right)=\dfrac{1}{2\sqrt{2}}\Leftrightarrow\dfrac{b}{b^2+2}=\dfrac{1}{2\sqrt{2}}\Leftrightarrow b^2+2=2\sqrt{2}b\Leftrightarrow b=\sqrt{2}\) (nhận)
Vậy \(max_{g\left(b\right)}=\dfrac{1}{2\sqrt{2}}\)
Làm tương tự với \(h\left(c\right)=\dfrac{c}{c^2+3}\), ta được \(max_{h\left(c\right)}=\dfrac{1}{2\sqrt{3}}\), xảy ra khi \(c=\sqrt{3}\)
Vậy GTLN của A là \(\dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}=\dfrac{6+3\sqrt{2}+2\sqrt{3}}{12}\), xảy ra khi \(\left(a,b,c\right)=\left(1,\sqrt{2},\sqrt{3}\right)\) hay \(\left(x,y,z\right)=\left(2,4,6\right)\).
Đúng 0
Bình luận (0)
Tìm giá trị nguyên của x để biểu thức P=\(\dfrac{4+\sqrt{x}}{1+\sqrt{x}}\) có giá trị lớn nhất
\(P=\dfrac{\sqrt{x}+1+3}{\sqrt{x}+1}=1+\dfrac{3}{\sqrt{x}+1}\)
P lớn nhất khi căn x+1=1
=>x=0
Đúng 0
Bình luận (0)
Cho biểu thức A = \(\dfrac{x+4}{\sqrt{x}+4}\) ; B = \(\left(\dfrac{x+3\sqrt{x}-3}{x-16}-\dfrac{1}{\sqrt{x}+4}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-4}\)
x ≥ 0, x ≠ 16
a) Rút gọn
b) Tìm giá trị nhỏ nhất của biểu thức \(\dfrac{A}{B}\)
(mink đag cần gấp)
a) Ta có: \(B=\left(\dfrac{x+3\sqrt{x}-3}{x-16}-\dfrac{1}{\sqrt{x}+4}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-4}\)
\(=\left(\dfrac{x+3\sqrt{x}-3-\sqrt{x}+4}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-4}\)
\(=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}\cdot\dfrac{\sqrt{x}-4}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+4}\)
Đúng 1
Bình luận (0)