Cho tứ giác ABCD có AB//CD và AB=CD .Chứng minh BC=AD và BC//AC
LC
Những câu hỏi liên quan
1/Cho tứ giác ABCD có AB//CD,AD//BC.Chứng minh AD=BC,AB=CD.
2/Cho tứ giác ABCD có AB//CD,AB=CD.Chứng minh AD//BC và AD=BC
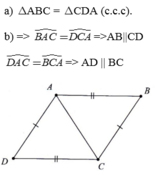
1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD thỏa mãn AB = CD, AD = BC. Chứng minh rằng:
a, △ABC = △CDA
b, AB // CD và AD // BC
~Có vẽ hình~
b: Xét tứ giác ABCD có
AB=CD
AD=BC
Do đó: ABCD là hình bình hành
Suy ra: AB//CD;AD//BC
Đúng 1
Bình luận (0)
Cho tứ giác ABCD có ^A+^C=60 và AB*CD=AD*BC. Chứng minh: AB*CD=AC*BD
Cho tứ giác ABCD thỏa mãn AB = CD, AD = BC. Chứng minh rằng:
a) ∆ A B C = ∆ C D A
b) AB // CD và AD // BC
Cho tứ giác ABCD, có AB // CD, AD // với BC. Chứng minh AB=CD, AD=BC
Xét tứ giác ABCD có
AB//CD
AD//BC
DO đó: ABCD là hình bình hành
Suy ra: AB=CD; AD=BC
Đúng 1
Bình luận (0)
Xét tứ giác ABCD có:
AD//BC
AB//CD
Suy ra: Tứ giác ABCD là hình bình hành vì có 2 cặp cạnh song song
Suy ra: AB=CD; AD=BC
Đúng 1
Bình luận (0)
Cho tứ giác ABCD có 2 đường chéo AC và BD vuông góc tại O
a. Chứng minh\(AB^{2} + CD^{2} = BC^{2} + AD^{2}
\)
b. Lấy các điểm M, N, P, Q thứ tự là trung điểm của AB, AC, CD, DA. Chứng Minh OM+ON+OQ=\(\dfrac{1}{2}\) (AB+BC+CD+DA)
a) \(AB^2+CD^2=OA^2+OB^2+OC^2+OD^2=\left(OA^2+OD^2\right)+\left(OB^2+OC^2\right)=AD^2+BC^2\)b) -Áp dụng định lí:
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng 1 nửa cạnh huyền.
\(OM+ON+OP+OQ=\dfrac{1}{2}AB+\dfrac{1}{2}BC+\dfrac{1}{2}CD+\dfrac{1}{2}DA=\dfrac{1}{2}\left(AB+BC+CD+DA\right)\)
Đúng 3
Bình luận (0)
tứ giác ABCD có AB=CD,BC=AD
a) chứng minh ABCD là hình thang cân
b)cho biết AC vuông góc BD và đường cao AH=4cm.Tính AB+CD
a)Tứ giác ABCD có AB=CD, AC=BD. Chứng minh ABCD là hình thang cân
b)Tứ giác ABCD có AD=AB=BC và ∠A+∠C=180°. Chứng minh ABCD là hình thang cân
Cho tứ giác ABCD có AB=CD;AD=BC
Chứng minh rằng:
A: tam giác ABC=tam giác CDA
B:AB//CD VÀ AD//BC
bài 5 : tứ giác abcd có ab+bd< hoặc =ac+cd
chứng minh :ab<ac
bài 6 :cho tứ giác abcd .chứng minh :
a) ab<bc+cd+ad b) ac+bd<ab+bc+cd+ad