A D B H C Hình 2
Cho hình 2, biết AB AC. Chứng minh rằng DB DC
Đọc tiếp
Cho hình 2, biết AB < AC. Chứng minh rằng DB < DC
NT
Những câu hỏi liên quan
Cho hình chữ nhật ABCD (AD AB) . Hai đường chéo AC và BD cắt nhau tại O. Qua D kẻ đường thẳng vuông góc với BD cắt tia BC tại E .a) Chứng minh tam giác BDE đồng dạng với tam giácDCE .b) Kẻ CH vuông góc với DE tại H . Chứng minh rằng: 2 . DC CH DB . Từ đó tínhđộ dài CH biết AD 6cm ; AB 8cm.c) Gọi K là giao điểm của OE và HC . Chứng minh:HK /ODEK/EO, từ đó suy ra: K là trung điểm của HC .d) Chứng minh ba đường thẳng ,, OE. CD .BH đồng quy
Đọc tiếp
Cho hình chữ nhật ABCD (AD <AB) . Hai đường chéo AC và BD cắt nhau tại O. Qua D kẻ đường thẳng vuông góc với BD cắt tia BC tại E .
a) Chứng minh tam giác BDE đồng dạng với tam giácDCE .
b) Kẻ CH vuông góc với DE tại H . Chứng minh rằng: 2 . DC CH DB = . Từ đó tính
độ dài CH biết AD = 6cm ; AB = 8cm.
c) Gọi K là giao điểm của OE và HC . Chứng minh:
HK /OD=EK/EO, từ đó suy ra: K là trung điểm của HC .
d) Chứng minh ba đường thẳng ,, OE. CD .BH đồng quy
a: Xét ΔBDE vuông tại D và ΔDCE vuông tại C có
góc E chung
=>ΔBDE đồng dạng với ΔDCE
b: BD=căn 8^2+6^2=10cm
BE=10^2/6=100/6=50/3cm
EC=DC^2/BC=8^2/6=32/3cm
Xét ΔEBD có CH//BD
nên CH/BD=EC/EB
=>CH/10=32/50=16/25
=>CH=160/25=6,4cm
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC .Trên tia AC lấy điểm M sao cho AM AB. Trên tia AB lấy điểm N sao cho AN AC. Chứng minh tứ giác BMCN là hình thangBài 2: Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh BC sao cho AM 1/2 BC, N là trung điểm cạnh AB. Chứng minh:a) Tam giác ABC cân ---- b) Tứ giác MNAC là hình thang vuông Bài 3: Cho hình thang cân ABCD ( AB // CD ) ---- a) Chứng minh góc ACD góc BCD ---- b) Gọi E là giao điểm của AC và BD. C/minh EA EBBài 4: Cho ABCD là hình thang ( AB // CD, AB CD...
Đọc tiếp
Bài 1: Cho tam giác ABC .Trên tia AC lấy điểm M sao cho AM = AB. Trên tia AB lấy điểm N sao cho AN = AC. Chứng minh tứ giác BMCN là hình thang
Bài 2: Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh BC sao cho AM= 1/2 BC, N là trung điểm cạnh AB. Chứng minh:
a) Tam giác ABC cân ---- b) Tứ giác MNAC là hình thang vuông
Bài 3: Cho hình thang cân ABCD ( AB // CD ) ---- a) Chứng minh góc ACD = góc BCD ---- b) Gọi E là giao điểm của AC và BD. C/minh EA = EB
Bài 4: Cho ABCD là hình thang ( AB // CD, AB < CD ). Kẻ các đường cao AE,BF của hình thang. C/minh rằng DE = CF
Bài 5: Cho ABCD là hình thang ( AB // CD ) có DB là đường phân giác góc D và AE là đường phân giác góc A ( E thuộc DC ). Biết AE // BC và O là giao điểm của AE với DB. CMR:
a) AE vuông góc với DB
b) AD // BE và AD = BE
c) E là trung điểm của DC
d) Xác định dạng của tứ giác BCEO
e) Biết góc BEC = 80 độ. Hãy tính các góc của hình thang ABCD
Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E
Đúng 0
Bình luận (0)
Quan sát Hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC.
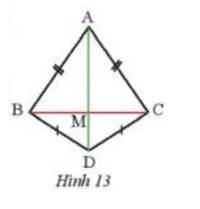
Xét tam giác ABD và tam giác ACD có :
AB = AC ( giả thiết )
BD = CD ( giả thiết )
AD cạnh chung
\( \Rightarrow \Delta ABD =\Delta ACD (c-c-c)\)
\( \Rightarrow \)\(\widehat {BAD} = \widehat {CAD}\)( 2 góc tương ứng )
Xét tam giác ABM và ta giác ACM có :
AB = AC ( giả thiết )
AM cạnh chung
\(\widehat {BAD} = \widehat {CAD}\)( chứng minh trên )
\(\Delta ABM=\Delta ACM (c-g-c)\)
\(\Rightarrow MC = MB\) ( 2 cạnh tương ứng )
\( \Rightarrow \) M là trung điểm BC
Đúng 0
Bình luận (0)
1)Cho hình bình hành ABCD, xác định các vectơ DA+DC,AB+DA.
2)Cho 5 điểm A, B, C, D, E. Chứng minh rằng: AC-ED+CD+EC-BC = AB
3)Cho hình vuông ABCD, tâm O cạnh bằng a.
a) Xác định vecto BA+DA+AC, AB+CA+BC, AB+AC.
b) Tính độ dài vecto DA+DC, AB-BC
Cho tam giác ABC vuông tại A có AH là đường cao (H thuộc BC).Biết AB 6cm,Bc10cma,chứng minh rằng tam giác HBA đồng dạng vs tam giác ABCb,Tính AC,AH,HBc,I và K lần lượt là hình chiếu của điểmH lên AB, AC. CHứng minh rằng AI .ABAK.ACd,Vẽ phân giác của tam giác AD của tam giác ABC ( D thuộc BC).Đường phân giác DE của tam giác ABD(E thuộc AB),đường phân giác DF của tam giác ADC(F thuộc AC) chứng minh rằng EA/EB*DB/DC*FC/FA1
Đọc tiếp
Cho tam giác ABC vuông tại A có AH là đường cao (H thuộc BC).Biết AB =6cm,Bc=10cm
a,chứng minh rằng tam giác HBA đồng dạng vs tam giác ABC
b,Tính AC,AH,HB
c,I và K lần lượt là hình chiếu của điểmH lên AB, AC. CHứng minh rằng AI .AB=AK.AC
d,Vẽ phân giác của tam giác AD của tam giác ABC ( D thuộc BC).Đường phân giác DE của tam giác ABD(E thuộc AB),đường phân giác DF của tam giác ADC(F thuộc AC) chứng minh rằng EA/EB*DB/DC*FC/FA=1
a) Xét t/giác HBA và t/giác ABC
có: \(\widehat{B}\):chung
\(\widehat{BHA}=\widehat{A}=90^0\)(gt)
=> t/giác HBA đồng dạng t/giác ABC (g.g)
b) Xét t/giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2 (định lí Pi - ta - go)
=> AC2 = BC2 - AB2 = 102 - 62 = 64
=> AC = 8 (cm)
Ta có: t/giác HBA đồng dạng t/giác ABC
=> HB/AB = AH/AC = AB/BC
hay HB/6 = AH/8 = 6/10 = 3/5
=> \(\hept{\begin{cases}HB=\frac{3}{5}.6=3,6\left(cm\right)\\AH=\frac{3}{5}.8=4,8\left(cm\right)\end{cases}}\)
c) Xét tứ giác AIHK có \(\widehat{A}=\widehat{AKH}=\widehat{AIH}=90^0\)
=> AIHK là HCN => \(\widehat{AIK}=\widehat{AHK}\)(cùng = \(\widehat{IKH}\)) (1)
Ta có: \(\widehat{AHK}+\widehat{KHC}=90^0\)(phụ nhau)
\(\widehat{KHC}+\widehat{C}=90^0\)(phụ nhau)
=> \(\widehat{AHK}=\widehat{C}\) (2)
Từ (1) và )2) => \(\widehat{AIK}=\widehat{C}\)
Xét t/giác AKI và t/giác ABC
có: \(\widehat{A}=90^0\): chung
\(\widehat{AIK}=\widehat{C}\)(cmt)
=> t/giác AKI đồng dạng t/giác ABC
=> AI/AC = AK/AB => AI.AB = AK.AC
d) Do AD là đường p/giác của t/giác ABC => \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{BC-DC}{DC}=\frac{BC}{DC}-1\)
<=> \(\frac{10}{DC}-1=\frac{6}{8}\) <=> \(\frac{10}{DC}=\frac{7}{4}\) <=> \(DC=\frac{40}{7}\)(cm)
=> BD = 10 - 40/7 = 30/7 (cm)
DE là đường p/giác của t/giác ABD => \(\frac{AD}{BD}=\frac{AE}{EB}\)(t/c đg p/giác)
DF là đường p/giác của t/giác ADC => \(\frac{DC}{AD}=\frac{FC}{AF}\)
Khi đó: \(\frac{EA}{EB}\cdot\frac{DB}{DC}\cdot\frac{FC}{FA}=\frac{AD}{DB}\cdot\frac{AB}{AC}\cdot\frac{DC}{AD}=\frac{AB\cdot DC}{BD.AC}=\frac{6\cdot\frac{40}{7}}{8\cdot\frac{30}{7}}=1\) (ĐPCM)
1. Cho hình thang ABCD có góc A góc D 90 độ , đáy nhỏ AB a , cạnh bên BC 2 a . Gọi M , N lần lượt là trung điểm AD , ABa / Tính số đo các góc ABC , BANb/ Chứng minh tam giác NAD đềuc/ Tính MN theo a 2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C 70 độ , góc D 40 độb/ Cho hình thang ABCD có AB // CD và góc A góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 AB^2 + CD^2 + 2AD^23. Cho tứ giác ABCD :a/ Chứng minh rằng AB + CD AC + BDb/ Cho biết AB + B...
Đọc tiếp
1. Cho hình thang ABCD có góc A = góc D = 90 độ , đáy nhỏ AB = a , cạnh bên BC = 2 a . Gọi M , N lần lượt là trung điểm AD , AB
a / Tính số đo các góc ABC , BAN
b/ Chứng minh tam giác NAD đều
c/ Tính MN theo a
2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C = 70 độ , góc D = 40 độ
b/ Cho hình thang ABCD có AB // CD và góc A = góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 = AB^2 + CD^2 + 2AD^2
3. Cho tứ giác ABCD :
a/ Chứng minh rằng AB + CD < AC + BD
b/ Cho biết AB + BD < hoặc = AC + CD
Chứng minh rằng AB < AC
4. Cho hình thang ABCD có AC vuông góc BD . CHứng minh rằng :
a/ AB^2 + CD^2 = AD^2 + BC^2
b/ ( AB + CD )^2 = AC^2 + BD^2
bạn hỏi thế này thì chả ai muốn làm -_- dài quá
Đúng 1
Bình luận (0)
Bạn gửi từng câu nhò thì các bạn khác dễ làm hơn!
Đúng 1
Bình luận (0)
dài quà làm sao mà có thòi gian mà trả lời .bạn hỏi ít thoi chứ
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Cho tam giác ABC vuông tại , đường phân giác AD. Tính độ dài AB,AC biết DB15cm, DC20cm.Bài 2: Cho hình bình hành ABCD (widehat{A} widehat{B}). Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD, H là hình chiếu của B trên AC. Chứng minh rằng:a) AB.AEAC.AHb) BC.AKAC.HCc) AB.AE+AD.AKAC^2Bài 3: Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB,AC theo thứ tự tại D và E. Gọi G là một điểm trên cạnh BC. Tính diện tích tứ giác ADGE nếu biết diện tích tam giác ABC1...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại , đường phân giác AD. Tính độ dài AB,AC biết DB=15cm, DC=20cm.
Bài 2: Cho hình bình hành ABCD (\(\widehat{A}< \widehat{B}\)). Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD, H là hình chiếu của B trên AC. Chứng minh rằng:
a) AB.AE=AC.AH
b) BC.AK=AC.HC
c) AB.AE+AD.AK=AC\(^2\)
Bài 3: Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB,AC theo thứ tự tại D và E. Gọi G là một điểm trên cạnh BC. Tính diện tích tứ giác ADGE nếu biết diện tích tam giác ABC=16\(cm^2\), diện tích tam giác ADE=9\(cm^2\)
cho tam giác abc có góc a =90 độ , đường cao ah ,gọi d,e theo thứ tự là hình chiếu vuông góc của h trên ab và ac , chứng minh rằng :
a) ab2 : ac2 =hb:hc
b) de 3 =bd.ce.bc
c) ab2 :ac3 =db;ec
Cho tam giác ABC vuông tại A có BC = 2.AB. E là trung điểm của BC. Tia phân giác góc B cắt AC ở D
a) Chứng minh DB là phân giác ADE
b) Chứng minh BD = DC
Nhớ vẽ thêm hình giúp mình nha
Bài 1: Cho tam giác ABC vuông tại , đường phân giác AD. Tính độ dài AB,AC biết DB15cm, DC20cm.Bài 2: Cho hình bình hành ABCD (widehat{A} widehat{B}). Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD, H là hình chiếu của B trên AC. Chứng minh rằng:a) AB.AEAC.AHb) BC.AKAC.HCc) AB.AE+AD.AKAC^2Bài 3: Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB,AC theo thứ tự tại D và E. Gọi G là một điểm trên cạnh BC. Tính diện tích tứ giác ADGE nếu biết diện tích tam giác ABC1...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại , đường phân giác AD. Tính độ dài AB,AC biết DB=15cm, DC=20cm.
Bài 2: Cho hình bình hành ABCD (\(\widehat{A}< \widehat{B}\)). Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD, H là hình chiếu của B trên AC. Chứng minh rằng:
a) AB.AE=AC.AH
b) BC.AK=AC.HCc) AB.AE+AD.AK=\(AC^2\)
Bài 3: Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB,AC theo thứ tự tại D và E. Gọi G là một điểm trên cạnh BC. Tính diện tích tứ giác ADGE nếu biết diện tích tam giác ABC=16\(cm^2\), diện tích tam giác ADE=9\(cm^2\)