Giáo điểm của 3 đuống cái gọi là
A trực tâm
B trọng tâm
C tâm đường tròn nội tiếp tam giác
Xét các khẳng định sau, tìm khẳng định đúng. Trong một tam giác giao điểm của ba trung tuyến gọi là:
A. Trọng tâm tam giác
B. Trực tâm tam giác
C. Tâm đường tròn ngoại tiếp tam giác
D. Tâm đường tròn nội tiếp tam giác
Cho ba điểm A(4; 3), B(2; 7) và C(-3; -8).
a, Tìm tọa độ trọng tâm G và trực tâm H của tam giác ABC;
b, Gọi T là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh T, G và H thẳng hàng.
c, Viết phương trình đường tròn ngoại tiếp tam giác ABC.
a)
– Tọa độ trọng tâm G của tam giác ABC là:
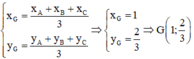
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận 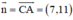 là một vtpt
là một vtpt
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận 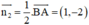 là một vtpt
là một vtpt
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:
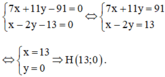
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
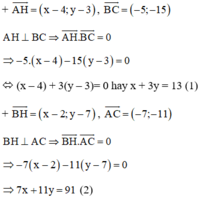
Từ (1) và (2) ta có hệ phương trình
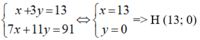
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
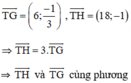
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
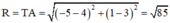
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:
(x + 5)2 + (y – 1)2 = 85
Xét các khẳng định sau. Tìm khẳng định đúng. Ba đường trung trực của một tam giác đồng qui tại một điểm gọi là:
A. Trọng tâm của tam giác
B. Tâm đường tròn ngoại tiếp
C. Trực tâm của tam giác
D. Tâm đường tròn nội tiếp
Câu 1: Xét các khẳng định sau, tìm khẳng định đúng. Trong một tam giác giao điểm của ba trung tuyến gọi là: A. Trọng tâm tam giác B. Trực tâm tam giác C. Tâm đường tròn ngoại tiếp tam giác D. Tâm đường tròn nội tiếp tam giác Câu 2: Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác. Độ dài trung tuyến AM là: A. 8cm B. √54cm C. √44cm D. 6cm Câu 3: Cho tam giác ABC, M là trung điểm của AC, G là trọng tâm của tam giác ABC và GM = 5cm. Độ dài đoạn BG là: A. 20cm B. 5cm C. 10cm D. 15cm Câu 4: Cho tam giác ABC có AB = AC = 13cm, BC = 10cm. Độ dài đường trung tuyến AM là: A. 12cm B. 10cm C. 8cm D. 6cm Câu 5: Trong một tam giác, điểm cách đều ba cạnh là: A. Giao điểm ba đường trung tuyến B. Giao điểm của ba đường trung trực C. Giao điểm ba đường phân giác D. Giao điểm ba đường cao Câu 6: Nếu một tam giác có một đường trung tuyến đồng thời là đường cao thì tam giác đó là: A. Tam giác vuông B. Tam nhọn C. Tam giác cân D. Tam giác tù Câu 7: Cho tam giác ABC, M là trung điểm của BC, G là trọng tâm của tam giác ABC và AM=18cm. Độ dài đoạn AG là: A. 12cm B. 6cm C. 9cm D. 10cm Câu 8: Cho tam giác ABC cân tại A, các đường trung tuyến BC và CE cắt nhau tại G. Chọn khẳng định đúng trong các khẳng định sau: A. AG là tia phân giác của góc A của tam giác ABC B. AG là đường trung trực của BC của tam giác ABC C. AG là đường cao của tam giác ABC D. Cả ba khẳng định đều đúng Câu 9: Cho tam giác ABC cân tại A, BC = 10cm. Độ dài đường trung tuyến AM bằng 12cm. Khi đó độ dài AB là A. 12cm B. 13cm C. 11cm D. 10cm Câu 10: Cho tam giác ABC vuông tại A. Trực tâm của tam giác ABC là điểm A. Nằm bên trong tam giác B. Nằm bên ngoài tam giác C. Là trung điểm của cạnh huyền BC D. Trùng với điểm A Câu 11: Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Cho AC = 10cm, BD = 4cm. Khi đó AD là: A. 6cm B. 4cm C. 3cm D. 5cm
Câu 1: B
Câu 2: C
Câu 3: C
Câu 4: A
Câu 5: D
Câu 6: B
Câu 7: C
Câu 8: D
Câu 1: Xét các khẳng định sau, tìm khẳng định đúng.
Trong một tam giác giao điểm của ba trung tuyến gọi là:
A. Trọng tâm tam giác
Câu 2: Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác. Độ dài trung tuyến AM là:
A. 8cm
Câu 3: Cho tam giác ABC, M là trung điểm của AC, G là trọng tâm của tam giác ABC và GM = 5cm. Độ dài đoạn BG là:
D. 15cm
Câu 4: Cho tam giác ABC có AB = AC = 13cm, BC = 10cm. Độ dài đường trung tuyến AM là:
A. 12cm
Câu 5: Trong một tam giác, điểm cách đều ba cạnh là:
C. Giao điểm ba đường phân giác
Câu 6: Nếu một tam giác có một đường trung tuyến đồng thời là đường cao thì tam giác đó là:
C. Tam giác cân
Câu 7: Cho tam giác ABC, M là trung điểm của BC, G là trọng tâm của tam giác ABC và AM=18cm. Độ dài đoạn AG là:
B. 6cm
Cho tam giác ABC nội tiếp đường tròn tâm O và điểm I là tâm đường tròn nội tiếp tam giác.Các điểm A', B', C' lần lượt là các giao điểm của AI,BI,CI với (O). Trên cung nhỏ AC của (O) không chứa điểm B lấy điểm D bất kì. Gọi E là giao điểm của DC' và AA', F là giao điểm củaDA' và CC'.CMR
a) I là trực tâm của tam giác A'B'C'
b) Tứ giác DEIF nội tiếp
c) Tâm đường tròn ngoại tiếp tam giác DEF luôn thuộc 1 đường thẳng cố định
a) Ta có ^AIC' = ^IAC + ^ICA = ^IAB + ^ICB = ^IAB + ^BAC' = ^IAC' => \(\Delta\)AC'I cân tại C'
=> C' nằm trên trung trực của AI. Tương tự B' cũng nằm trên trung trực của AI => B'C' vuông góc AI
Hay A'I vuông góc với B'C'. Lập luận tương tự B'I vuông góc A'C', C'I vuông góc A'B'
Do đó I là trực tâm của \(\Delta\)A'B'C' (đpcm).
b) Ta thấy ^FDE = ^A'DC' = ^A'AC' = ^IAC' = C'IA (Vì \(\Delta\)AC'I cân tại C') = ^EIC'
Suy ra tứ giác DEIF nội tiếp (đpcm).
c) Gọi S là tâm ngoại tiếp của \(\Delta\)DEF. Vì tứ giác DEIF nội tiếp (cmt) nên S đồng thời là tâm ngoại tiếp DEIF
Gọi giao điểm thứ hai giữa (S) và (O) là G. Khi đó ^DFG = ^DEG => ^GFA' = ^GEC'
Lại có ^EGF = ^EDF = ^A'DC' = ^A'GC' => ^FGA' = ^EGC'. Do vậy \(\Delta\)GEC' ~ \(\Delta\)GFA' (g.g)
=> \(\frac{GC'}{GA'}=\frac{EC'}{FA'}\). Mặt khác ^A'IF = ^C'IA = ^C'AI = ^C'AE và ^IA'F = ^AA'D = ^AC'D = ^AC'E
Cho nên \(\Delta\)AEC' ~ \(\Delta\)IFA' (g.g) => \(\frac{EC'}{FA'}=\frac{AC'}{IA'}\). Mà các điểm A,I,A',C' đều cố định
Nên tỉ số \(\frac{AC'}{FA'}\) là bất biến. Như vậy \(\frac{GC'}{GA'}\)không đổi, khi đó tỉ số giữa (GC' và (GA' của (O) không đổi
Kết hợp với (O), A',C' cố định suy ra G là điểm cố định. Theo đó trung trực của IG cố định
Mà S thuộc trung trực của IG (do D,I,E,F,G cùng thuộc (S)) nên S di động trên trung trực của IG cố định (đpcm).
Cho tam giác ABC có các góc là góc nhọn và nội tiếp đường tròn tâm (O). Tiếp tuyến của đường tròn tâm (O) tại B,C cắt nhau tại D
a) Chứng minh OCDB nội tiếp
b) Gọi H là trực tâm của tam giác ABC. M là trung điểm của BC
Chứng minh AH=2OM
a) Xét tứ giác OCDB có
\(\widehat{OBD}+\widehat{OBC}=180^0\)
Do đó: OCDB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Cho hình chóp S.ABCD, SA = SB = SC. Gọi O là hình chiếu của S trên (ABC). Hỏi mệnh đề nào sau đây đúng?
A. O là trọng tâm tam giác ABC.
B. O là trực tâm tam giác ABC.
C. O là tâm đường tròn ngoại tiếp tam giác ABC.
D. O tâm đường tròn nội tiếp tam giác ABC.
Cho hình chóp S.ABCD, SA = SB = SC. Gọi O là hình chiếu của S trên (ABC). Hỏi mệnh đề nào sau đây đúng?
A. O là trọng tâm tam giác ABC.
B. O là trực tâm tam giác ABC.
C. O là tâm đường tròn ngoại tiếp tam giác ABC.
D. O tâm đường tròn nội tiếp tam giác ABC.
Do \(SO\perp ABC\Rightarrow\) các tam giác SOA, SOB, SOC đều vuông tại O
Đặt \(SA=SB=SC=a\) , áp dụng Pitago:
\(OA=\sqrt{SA^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OB=\sqrt{SB^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OC=\sqrt{SC^2-SO^2}=\sqrt{a^2-SO^2}\)
\(\Rightarrow OA=OB=OC\Rightarrow O\) là tâm đường tròn ngoại tiếp tam giác ABC
Câu 1: Xét các khẳng định sau, tìm khẳng định đúng. Trong một tam giác giao điểm của ba trung tuyến gọi là: A. Trọng tâm tam giác B. Trực tâm tam giác C. Tâm đường tròn ngoại tiếp tam giác D. Tâm đường tròn nội tiếp tam giác Câu 2: Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác. Độ dài trung tuyến AM là: A. 8cm B. √54cm C. √44cm D. 6cm Câu 3: Cho tam giác ABC, M là trung điểm của AC, G là trọng tâm của tam giác ABC và GM = 5cm. Độ dài đoạn BG là: A. 20cm B. 5cm C. 10cm D. 15cm Câu 4: Cho tam giác ABC có AB = AC = 13cm, BC = 10cm. Độ dài đường trung tuyến AM là: A. 12cm B. 10cm C. 8cm D. 6cm Câu 5: Trong một tam giác, điểm cách đều ba cạnh là: A. Giao điểm ba đường trung tuyến B. Giao điểm của ba đường trung trực C. Giao điểm ba đường phân giác D. Giao điểm ba đường cao Câu 6: Nếu một tam giác có một đường trung tuyến đồng thời là đường cao thì tam giác đó là: A. Tam giác vuông B. Tam nhọn C. Tam giác cân D. Tam giác tù Câu 7: Cho tam giác ABC, M là trung điểm của BC, G là trọng tâm của tam giác ABC và AM=18cm. Độ dài đoạn AG là: A. 12cm B. 6cm C. 9cm D. 10cm Câu 8: Cho tam giác ABC cân tại A, các đường trung tuyến BC và CE cắt nhau tại G. Chọn khẳng định đúng trong các khẳng định sau: A. AG là tia phân giác của góc A của tam giác ABC B. AG là đường trung trực của BC của tam giác ABC C. AG là đường cao của tam giác ABC D. Cả ba khẳng định đều đúng Câu 9: Cho tam giác ABC cân tại A, BC = 10cm. Độ dài đường trung tuyến AM bằng 12cm. Khi đó độ dài AB là A. 12cm B. 13cm C. 11cm D. 10cm Câu 10: Cho tam giác ABC vuông tại A. Trực tâm của tam giác ABC là điểm A. Nằm bên trong tam giác B. Nằm bên ngoài tam giác C. Là trung điểm của cạnh huyền BC D. Trùng với điểm A Câu 11: Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Cho AC = 10cm, BD = 4cm. Khi đó AD là: A. 6cm B. 4cm C. 3cm D. 5cm
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O và trực tâm H. Kẻ đường kính AD.
a/ Chứng minh tứ giác BHCD là hình bình hành
B/ Gọi I lầ trung điểm BC. Chứng minh: AH = 2OI
C/ Chứng minh: O,B là trọng tâm G của tam giác ABC là ba điểm thẳng hàng.
a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD vuông góc AB
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC vuông góc CD
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔHDA có
I,O lần lượt là trung điểm của DH,DA
=>IO là đường trung bình
=>IO//AH và IO=AH/2
=>AH=2IO