Đo các góc \(CED,CGD,BED,GCE\) ở hình 5
SK
Những câu hỏi liên quan
Đo các góc CED, CGD, BED, DCE ở hình dưới
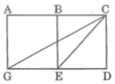
Dùng thước đo góc, chúng ta đo được số đo các góc như sau:
Đúng 0
Bình luận (0)
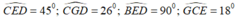
do cac goc CED,CGD,BED,GCE
tứ giác ABCD có góc A=110 độ; góc B=100 độ. Các đường phân giác của góc ngoài tại đỉnh C và D cắt nhau ở E. Góc CED có số đo là?
tứ giác ABCD có góc A+B=200 độ .các tai p|g của các góc C và D cắt nhau ở E.các tia p|g của các góc ngoài C và D cắt nhau ở F .tính số đo các góc CED và CFD GIÚP MÌNH VỚI CẢM ƠN
Cho tam giác ABC cân đỉnh B, biết một góc ở đáy có số đo 80 độ . Từ A và C người ta kẻ hai đường thẳng cắt các cạnh đối diện theo thứ tự ở D và E sao cho góc CAD=60 độ , góc ACE=70 độ. Tính góc CED
b1. Tứ giác ABCD có góc C= 60*, góc D = 80*; góc A - góc B = 10*. Tính số đo góc A và B.
b2. tứ giác ABCD có góc A = 110*; góc B = 100*. Các tia phân giác của góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau ở F. Tính CED và CFD?
Bài 1 : Bài giải
Ta có : \(\widehat{A}-\widehat{B}=10^o\text{ }\Rightarrow\text{ }\widehat{A}=\widehat{B}+10^o\)
Trong tứ giác ABCD có :
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{B}+10+\widehat{B}+60^o+80^o=360^o\)
\(2\widehat{B}+150^o=360^o\)
\(2\widehat{B}=110^o\)
\(\widehat{B}=55^o\text{ }\Rightarrow\text{ }\widehat{A}=65^o\)
Cho tứ giác ABCD có 2 góc đói bù nhau. Các cạnh AD và BC căt nhau ở E, AB và DC cắt nhau ở F. Phân giác góc CED và phân giác góc AFD cắt nhau ở M. Chứng minh FM vuông góc với EM( chỉ cần vẽ hình thôi!!!!)
http://pitago.vn/question/cho-tu-giac-abcd-co-cac-goc-bu-nhau-hai-duong-thang-ad-bc-49638.html
trong link này có hình
chúc học tốt
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A ,có góc BAC=80 độ .Các điểm D,E theo thứ tự thuộc các cạnh BC,CA sao cho góc BAD=ABE=30 độ . Tính số đo của góc BED. ( Vẽ hình rồi tính ).
Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó.
Vì AD vuông góc với hai đáy AB và CD nên \(\widehat{A}=\widehat{D}=90^0\)
Vì ABCD có 2 đáy AB,CD nên AB // CD. Do đó, \(\widehat B + \widehat C = 180^\circ \) ( 2 góc trong cùng phía)
Mặt khác:
\(\begin{array}{l}\widehat B = 2.\widehat C\\ \Rightarrow 2.\widehat C + \widehat C = 180^\circ \\ \Rightarrow 3.\widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ :3 = 60^\circ \end{array}\)
\(\Rightarrow \widehat B = 2. \widehat{C}=2.60^0=120^0\)
Vậy \(\widehat{A}=\widehat{D}=90^0; \widehat B = 120^0; \widehat C =60^0\)
Đúng 0
Bình luận (0)