cac bạn dúp mình â câu cuối ạ, mình cảm ơn
TN
Những câu hỏi liên quan
Bạn nào giúp mik 1 hoặc 2 câu cuối đk ạ. Mình cảm ơn nhiều
Câu cuối bài hình ạ, mình cảm ơn
\(\widehat{AEI}=\widehat{BEI}\) (chắn 2 cung bằng nhau AC và BC)
\(\Rightarrow\) theo định lý phân giác: \(\dfrac{EB}{AE}=\dfrac{IB}{IA}=\dfrac{\dfrac{R}{2}}{R+\dfrac{R}{2}}=\dfrac{1}{3}\)
Mặt khác 2 tam giác vuông AOH và AEB đồng dạng (chung góc A)
\(\Rightarrow\dfrac{OH}{OA}=\dfrac{EB}{AE}=\dfrac{1}{3}\)
Lại có \(OA=OD\Rightarrow OH=\dfrac{1}{3}OD\Rightarrow DH=\dfrac{2}{3}OD\)
O lại là trung điểm AB \(\Rightarrow H\) là trọng tâm ABD
\(\Rightarrow AH\) đi qua trung điểm BD hay K là trung điểm BD
Mà tam giác OBD vuông cân tại O \(\Rightarrow\) OK là trung tuyến đồng thời là đường cao
\(\Rightarrow OK\perp BD\)
Đúng 4
Bình luận (12)
Cho các số thực x,y,z thỏa mãn x,y,z \(\ge\) 1 và \(3\left(x+y+z\right)=x^2+y^2+z^2+2xy\)
Tìm Min: \(P=\dfrac{x^2}{\left(x+y\right)^2+x}+\dfrac{x}{z^2+x}\)
Đúng 0
Bình luận (6)
Giúp mình làm Câu c) bài hình và bài cuối với ạ, mình cảm ơn :3
Nhanh một chút ạ, mình đang cần

Câu 4:
D và F cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF)
Tương tự, ABDE nội tiếp \(\Rightarrow\widehat{ABE}=\widehat{ADE}\) (cùng chắn AE)
Lại có \(\widehat{ABE}=\widehat{ACF}\) (cùng phụ góc \(\widehat{A}\))
\(\Rightarrow\widehat{ADE}=\widehat{ADF}\) hay AD là phân giác góc \(\widehat{FDE}\)
./
Hoàn toàn tương tự, ta cũng có CF là phân giác \(\widehat{DFE}\Rightarrow\widehat{BFD}=\widehat{AFE}\)
Mà \(\widehat{AFE}=\widehat{BFK}\Rightarrow\widehat{BFK}=\widehat{BFD}\)
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{FK}{FD}\) theo định lý phân giác
Đồng thời \(\dfrac{CK}{CD}=\dfrac{FK}{FD}\) (CF là phân giác ngoài góc \(\widehat{DFK}\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{CK}{CD}\Rightarrow\dfrac{BK}{CK}=\dfrac{BD}{CD}\)
Qua B kẻ đường thẳng song song AC cắt AK và AD tại P và Q
Theo Talet: \(\dfrac{BK}{CK}=\dfrac{BP}{AC}\) đồng thời \(\dfrac{BD}{DC}=\dfrac{BQ}{AC}\)
\(\Rightarrow\dfrac{BP}{AC}=\dfrac{BQ}{AC}\Rightarrow BP=BQ\)
Mặt khác BP song song MF (cùng song song AC)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{AF}{AB}\) ; \(\dfrac{NF}{BQ}=\dfrac{AF}{AB}\) (Talet)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{NF}{BQ}\Rightarrow MF=NF\)
Đúng 1
Bình luận (3)
Câu 5:
ĐKXĐ: \(-1\le x\le1\)
Đặt \(\sqrt{1+x}+\sqrt{1-x}=t>0\)
\(\Rightarrow t^2=1+x+1-x+2\sqrt{\left(1+x\right)\left(1-x\right)}=2+2\sqrt{1-x^2}\)
Do đó pt trở thành:
\(t.t^2=8\Leftrightarrow t^3=8\)
\(\Leftrightarrow t=2\Leftrightarrow\sqrt{1-x}+\sqrt{1+x}=2\)
\(\Leftrightarrow2+2\sqrt{1-x^2}=4\Leftrightarrow\sqrt{1-x^2}=1\)
\(\Leftrightarrow1-x^2=1\)
\(\Leftrightarrow x=0\)
Đúng 1
Bình luận (0)
các bạn giúp mình câu b ạ, mình cảm ơn
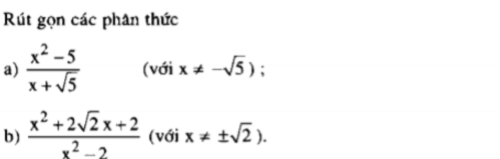
b) \(\dfrac{x^2+2\sqrt{2}x+2}{x^2-2}=\dfrac{\left(x+\sqrt{2}\right)^2}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}=\dfrac{x+\sqrt{2}}{x-\sqrt{2}}\)
Đúng 1
Bình luận (0)
a, \(\dfrac{x^2-5}{x+\sqrt{5}}=\dfrac{\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)}{x+\sqrt{5}}=x-\sqrt{5}\)
Đúng 1
Bình luận (0)
 Các bạn giúp mình câu c ạ, mình cảm ơn
Các bạn giúp mình câu c ạ, mình cảm ơn
các bạn giúp mình câu này với mình cảm ơn ạ

Các bạn giúp mình câu này với ạ. Mình cảm ơn 
Các bạn hộ mình câu 1 với ạ. Mình cảm ơn!
Các bạn giải và giải thích từng câu giúp mình với ạ. Mình cảm ơn ạ
12.
\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\le\sqrt[]{2}\)
\(\Rightarrow M=\sqrt{2}\)
13.
Pt có nghiệm khi:
\(5^2+m^2\ge\left(m+1\right)^2\)
\(\Leftrightarrow2m\le24\)
\(\Rightarrow m\le12\)
Đúng 0
Bình luận (0)
14.
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{5}{3}\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x=k2\pi\)
15.
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)
Đáp án A
16.
\(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
\(\left[{}\begin{matrix}2\pi\le\dfrac{\pi}{3}+k2\pi\le2018\pi\\2\pi\le\pi+k2\pi\le2018\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}1\le k\le1008\\1\le k\le1008\end{matrix}\right.\)
Có \(1008+1008=2016\) nghiệm
Đúng 1
Bình luận (0)






