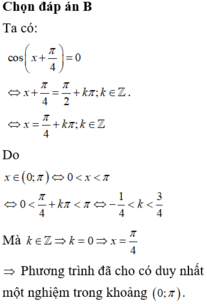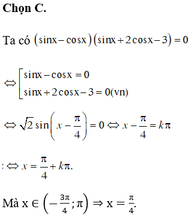CMR pt x2 cosx+xsinx+1=0 có ít nhất 1 nghiệm thuộc khoảng (0, π)
SM
Những câu hỏi liên quan
Phương trình cos 2 x + cos x = 0 có bao nhiêu nghiệm thuộc khoảng − π ; π
A. 1
B. 4
C. 2
D. 3
Đáp án C.
Phương pháp
Sử dụng tính chất hai góc bù nhau cos x = cos π − x
Giải phương trình lượng giác cơ bản
Cách giải
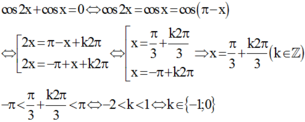
Vậy phương trình có 2 nghiệm thuộc − π ; π
Đúng 0
Bình luận (0)
Số nghiệm thuộc nửa khoảng [ - π ; 0 ) của phương trình cosx-cos2x-cos3x+1 = 0 là
A. 3.
B. 1.
C. 4.
D. 2.
Chọn D
Phương trình tương với:
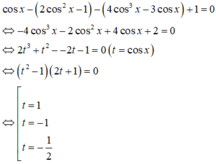
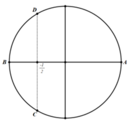
Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng [ - π ; 0 ) , phương trình có đúng 2 nghiệm (là - π và - 2 π 3 ).
Đúng 0
Bình luận (0)
Số nghiệm thuộc nửa khoảng
[
−
π
;
0
)
của phương trình
cos
x
−
cos
2
x
−
cos
3
x
+
1
0
là A. 3 B. 1 C. 4 D. 2
Đọc tiếp
Số nghiệm thuộc nửa khoảng [ − π ; 0 ) của phương trình cos x − cos 2 x − cos 3 x + 1 = 0 là
A. 3
B. 1
C. 4
D. 2
Đáp án D.
Phương trình tương với:
cos x − 2 cos 2 x − 1 − 4 cos 3 x − 3 cos x + 1 = 0 ⇔ − 4 cos 3 x − 2 cos 2 x + 4 cos x + 2 = 0 ⇔ 2 t 3 + t 2 − − 2 t − 1 = 0 t = cos x ⇔ t 2 − 1 2 t + 1 = 0 ⇔ t = 1 t = − 1 t = − 1 2
Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng − π ; 0 , phương trình có đúng 2 nghiệm (là − π và − 2 π 3 ).
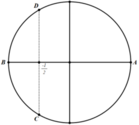
Đúng 0
Bình luận (0)
Tìm số nghiệm thuộc khoảng - π ; π của phương trình cosx + sin2x = 0
A. 4
B. 3
C. 1
D. 2
Đáp án A
Ta có c o s x + sin 2 x = 0 ⇔ cos x + 2 sin x cos x = 0 ⇔ [ cos x = 0 sin x = - 1 2 ⇔ [ x = π 2 + k π x = - π 6 + k 2 π x = 7 π 6 + k 2 π
Mà x ∈ - π ; π ⇒ x ∈ - π 2 ; π 2 ; - π 6 ; - 5 π 6 .
Đúng 0
Bình luận (0)
Tìm số nghiệm thuộc khoảng
0
;
π
của phương trình
cos
x
+
π
4
0
A. 0. B. 1. C. 2. D. 3.
Đọc tiếp
Tìm số nghiệm thuộc khoảng 0 ; π của phương trình cos x + π 4 = 0
A. 0.
B. 1.
C. 2.
D. 3.
Số nghiệm thuộc nửa khoảng
-
π
;
0
của phương trình
cos
x
-
cos
2
x
-
cos
3
x
0
là
Đọc tiếp
Số nghiệm thuộc nửa khoảng - π ; 0 của phương trình cos x - cos 2 x - cos 3 x = 0 là
![]()
![]()
![]()
![]()
98. Nghiệm của pt -2cos2x =1 là?
97. Pt cosx=0 có bao nhiêu nghiệm thuộc khoảng (0;2018π)
96. Pt sinx=1 có bn nghiệm thuộc khoảng (0;2018π)
93. Nghiệm của pt sin(π.cosx)=1 là?
91. Pt sin = a luôn có nghiệm khi nào?
98:
$-2\cos 2x=1$
$\Leftrightarrow \cos 2x=\frac{-1}{2}$
\(\Rightarrow \left[\begin{matrix} 2x=\frac{2}{3}\pi +2k\pi\\ 2x=\frac{-2}{3}\pi +2k\pi\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{\pi}{3}+k\pi\\ x=\frac{-\pi}{3}+k\pi \end{matrix}\right.\) với $k$ nguyên.
Đúng 0
Bình luận (0)
97:
$\cos x=0\Rightarrow x=\pi (k+\frac{1}{2})$ với $k\in \mathbb{Z}$
Vì $x\in (0;2018\pi)$ nên $0< \pi (k+\frac{1}{2})< 2018\pi$
$\Leftrightarrow 0< k+\frac{1}{2}< 2018$
$\Leftrightarrow \frac{-1}{2}< k< \frac{4035}{2}$
Vì $k$ nguyên nên $k\in\left\{0;1;2;...; 2017\right\}$
Có 2018 giá trị của $k$ thỏa mãn kéo theo có 2018 giá trị $x$ thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
96:
$\sin x=1\Rightarrow x=\pi (\frac{1}{2}+2k)$ với $k$ là số nguyên.
$x\in (0;2018\pi)$
$\Leftrightarrow \frac{1}{2}+2k\in (0;2018)$
$\Leftrightarrow k\in (-\frac{1}{4};\frac{4035}{4})$
Vì $k$ nguyên nên $k\in\left\{0;1;...;1008\right\}$
Như vậy có 1009 giá trị $k$ thỏa mãn kéo theo có 1008 giá trị $x$
Vậy có 1009 nghiệm của PT $\sin x=1$ thuộc khoảng $(0;2018\pi)$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Phương trình sin x + cos x = 1 có bao nhiêu nghiệm trên khoảng 0 ; π .
A. 1
B. 0
C. 2
D. 3
Phương trình (sinx - cosx)(sinx + 2cosx - 3) 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng
-
3
π
4
;
π
? A. 3 B. 0. C. 1. D. 2.
Đọc tiếp
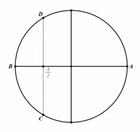
Phương trình (sinx - cosx)(sinx + 2cosx - 3) = 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng - 3 π 4 ; π ?
A. 3
B. 0.
C. 1.
D. 2.