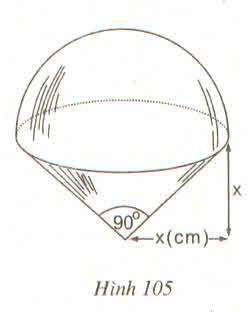
Trong nửa hình cầu (h.103) có \(OR=x\left(cm\right);\widehat{TOS}=45^0\)
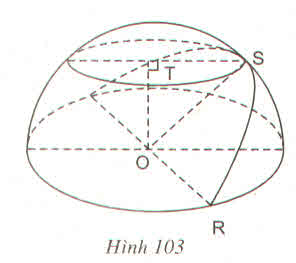
Độ dài đoạn ST nhận giá trị nào trong các giá trị sau :
(A) \(x\left(cm\right)\) (B) \(\sqrt{2}x\left(cm\right)\)
(C) \(\dfrac{x}{\sqrt{2}}\left(cm\right)\) (D) \(2x\left(cm\right)\)