 giúp mik nhanh nhanh nha
giúp mik nhanh nhanh nha
NP
Những câu hỏi liên quan
mng làm nhanh giúp mik nha , mik đang càn gắp nha , ai làm nhanh mik tick nha
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
Đúng 2
Bình luận (0)
giúp mik với. tính giá trị của biểu thức nha. nhanh nhanh giúp mik ạ
Đọc tiếp
giúp mik với. tính giá trị của biểu thức nha. nhanh nhanh giúp mik ạ
\(=11\cdot\dfrac{16}{55}\cdot\dfrac{15}{8}=\dfrac{11\cdot5}{55}\cdot\dfrac{16}{8}\cdot3=2\cdot3=6\)
Đúng 0
Bình luận (0)
các bạn ơi giúp mik với bạn nào trả lời nhanh mik tik nha nhanh nha ![]()


giúp mik nhanh nhanh nha
a: Xét ΔBAD và ΔBHD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó; ΔBAD=ΔBHD
Suy ra: \(\widehat{BAD}=\widehat{BHD}=90^0\)
hay DH⊥BC
b: \(\widehat{ABC}=180^0-110^0=70^0\)
nên \(\widehat{ABD}=35^0\)
Đúng 1
Bình luận (0)
mng làm nhanh giúp mik vs ah , ai nhanh mik tick nha
Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k$
$\Rightarrow a=bk, c=dk$. Khi đó:
$\frac{a-b}{b}=\frac{bk-b}{b}=\frac{b(k-1)}{b}=k-1(1)$
$\frac{c-d}{d}=\frac{dk-d}{d}=\frac{d(k-1)}{d}=k-1(2)$
Từ $(1); (2)\Rightarrow \frac{a-b}{b}=\frac{c-d}{d}$
-------------------
$\frac{2a+3b}{2a-3b}=\frac{2bk+3b}{2bk-3b}=\frac{b(2k+3)}{b(2k-3)}=\frac{2k+3}{2k-3}(3)$
$\frac{2c+3d}{2c-3d}=\frac{2dk+3d}{2dk-3d}=\frac{d(2k+3)}{d(2k-3)}=\frac{2k+3}{2k-3}(4)$
Từ $(3); (4)\Rightarrow \frac{2a+3b}{2a-3b}=\frac{2c+3d}{2c-3d}$
Đúng 1
Bình luận (0)
24*8:6=
Nhanh giúp mik nha mn ai nhanh mik tick cho
Xem thêm câu trả lời
Mng làm nhanh giúp mik vs ah, mik đg cần gấp ah, ai nhanh mik tik nha <3
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
Đúng 0
Bình luận (0)
Giúp mik vs mik đang cần gấp nhanh lên nha giúp mik!!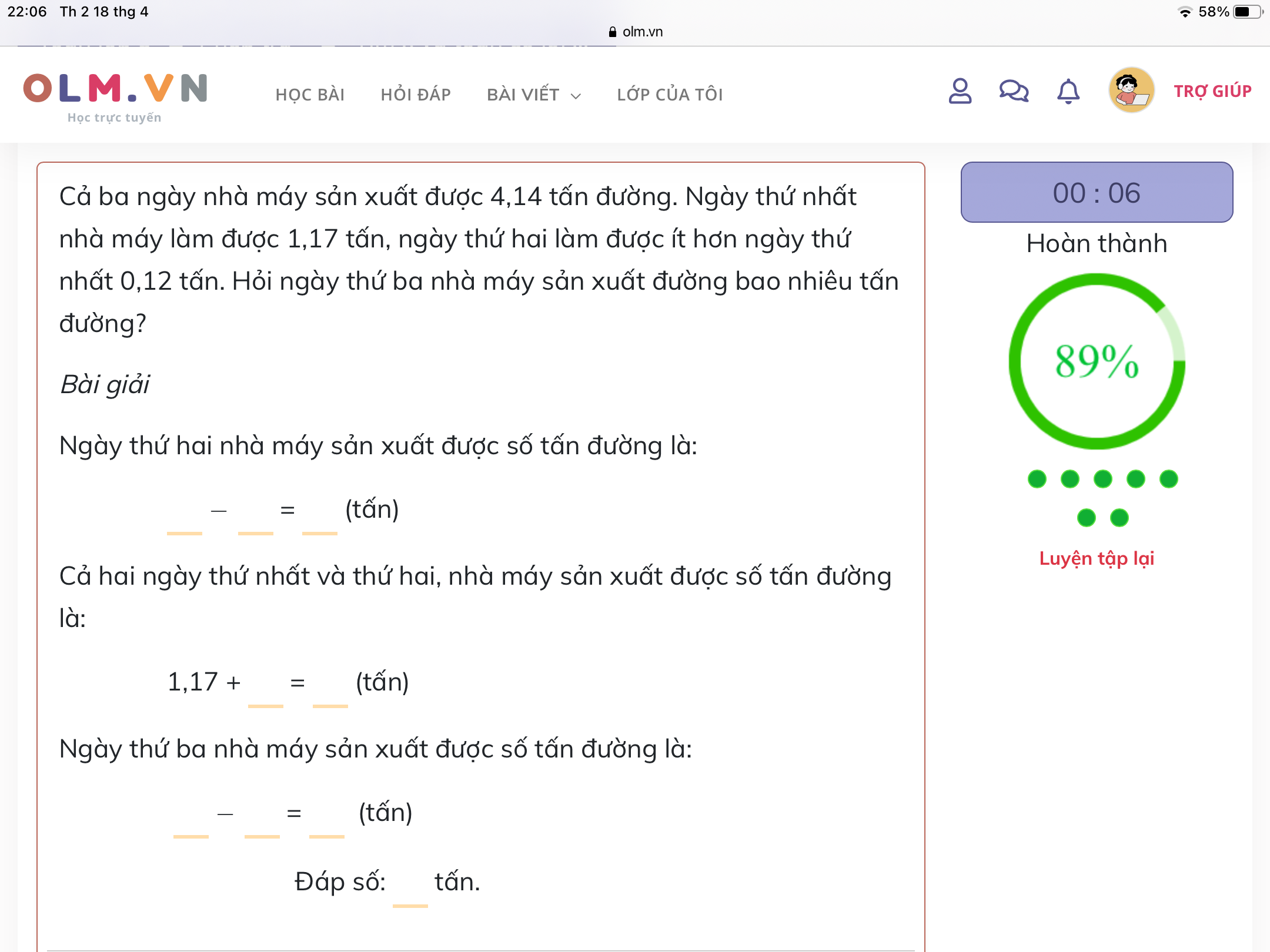
Ngày thứ hai nhà máy sản xuất được số tấn đường là:
1,17-0,12= 1,05 (tấn)
Cả hai ngày thứ nhất và thứ hai, nhà máy sản xuất được số tấn đương là:
1,17+1,05=2,22 (tấn)
Ngày thứ ba nhà máy sản xuất được số tấn đường là:
4,14-2,22=1,92 (tấn)
"Chúc em học tốt."
Đúng 0
Bình luận (0)
Các bn giải tất cả các bài trên ảnh nha
Giai nhanh nhanh giúp mik nha mik đang cần gấp
Ai giải dc thì mik cho 1 vé kb và 1 GP nha

Ảnh có tí xíu à bạn.
Giúp mik với bí rồi ai nhanh mik tick nha cần gấp ngay hôm nay ! giải chi tiết hộ mik đi nha !!
Chứng minh : 1/2 < 1/51 + 1/52 + ... + 1/00 < 1
Nhanh nha ! mik sẽ tick cho ng nhanh nhất
1/51+1/52+1/53+....+1/100>1/100+1/100+1/100+...+1/100(50 so 0)=50/100=1/2
Đúng 0
Bình luận (0)
Ta thấy:
151<150151<150
152<150152<150
...
1100<1501100<150
⇒151+152+...+1100<150.50=1⇒151+152+...+1100<150.50=1
⇒151+152+...+1100<1(1)⇒151+152+...+1100<1(1)
Lại có:
151>1100151>1100
152>1100152>1100
...
1100=11001100=1100
⇒151+152+...+1100>1100.50=12⇒151+152+...+1100>1100.50=12
⇒151+152+...+1100>12(2)⇒151+152+...+1100>12(2)
Từ (1),(2)⇒⇒12<151+152+...+1100<1
/HT\



