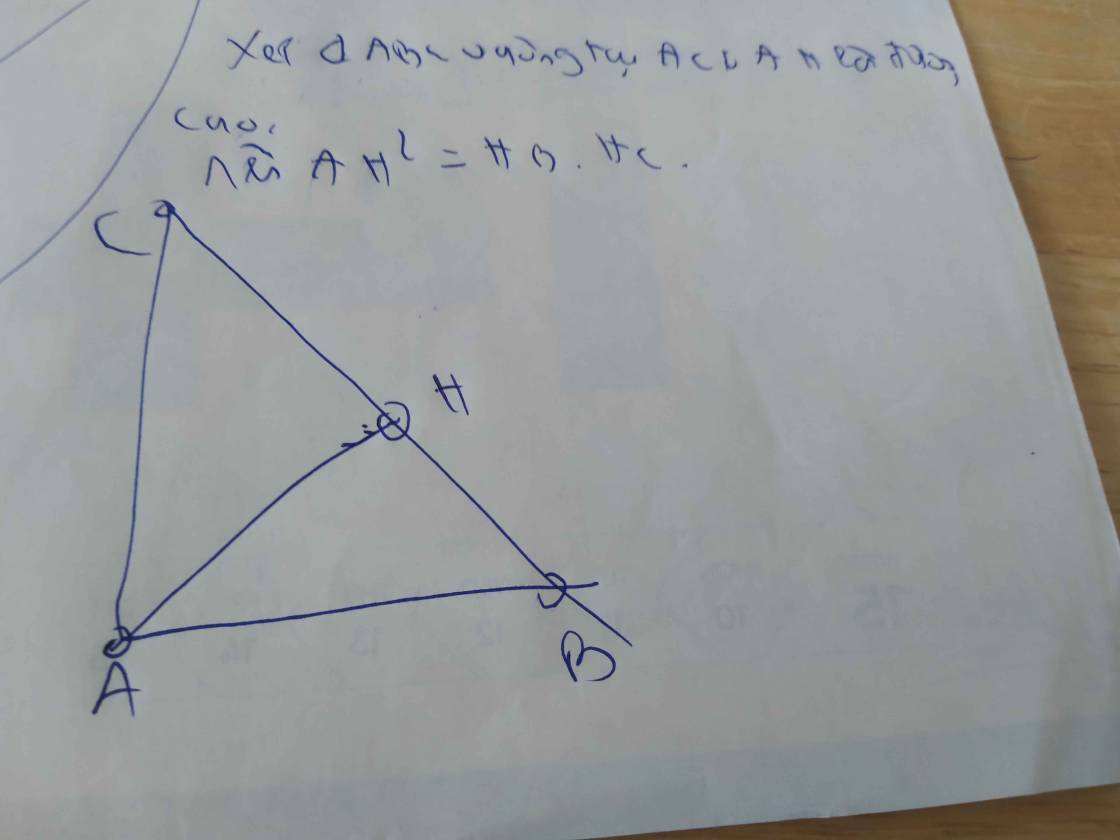
Dựng tam giác ABC cân tại A, biết BC = 3cm, đường cao BH = 2,5 cm
SK
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A , đường cao AH a, Biết AH = 6 cm , BH = 4,5 cm . Tính AB , AC , BC, HC b, Biết AB=6 cm , BH = 3cm . Tính AH , AC ,HC
Dựng ΔABC cân tại A, biết BC = 3cm, đường cao BH = 2,5cm.
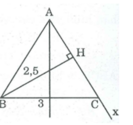
Cách dựng:
- Dựng BH : 2,5cm
- Dựng ∠ (xHB) = 90 0
- Dựng cung tròn tâm B bán kính 3cm cắt Hx tại C.
- Dựng BC
- Dựng đường trung trực BC cắt CH tại A
- Dựng AB, ta có ∆ ABC cẩn dựng
Chứng minh:
Ta có AC = AB (tính chất đường trung trực)
Nên ∆ ABC cân tại A, BH ⊥ AC
Ta lại có BC = 3cm, BH = 2,5cm
Vậy ∆ ABC dựng được thỏa mãn điều kiện bài toán.
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. a) Biết AB 9cm, BC 15cm. Tính BH, HC b) Biết BH 1cm, HC 3cm. Tính AB, AC c) Biết AB 6cm, AC 8cm. Tính AH, BCBài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 3cm, BH 2,4cm a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc BBài 3: Cho tam giác ABC có BC 9cm, góc B 60 độ, góc C 40 độ, đường cao AH. Tính AH, AB, AC
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB= 9cm, BC= 15cm. Tính BH, HC
b) Biết BH= 1cm, HC= 3cm. Tính AB, AC
c) Biết AB= 6cm, AC= 8cm. Tính AH, BC
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB= 3cm, BH= 2,4cm
a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc B
Bài 3: Cho tam giác ABC có BC= 9cm, góc B= 60 độ, góc C= 40 độ, đường cao AH. Tính AH, AB, AC
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A; đường cao AH ( H thuộc BC ) và phân giác CM ( M thuộc AB ). N là giao điểm AH và CM. Biết BH = 3cm; HC = 27cm. Chứng minh AH2 = BH x HC
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HM ⊥ AB;HN ⊥ AC. Biết AB = 3cm; AC = 4 cm
a) Tính BC, BH, CH, MN
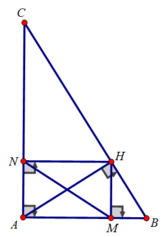
a) Xét tam giác ABC vuông tại A, đường cao AH có:
B C 2 = A B 2 + A C 2 = 25 ⇒ BC = 5(cm)
AB2 = BH.BC ⇒ BH = AB2/BC = 9/5 = 1,8(cm)
BH + CH = BC⇒ CH = BC - BH = 5 - 1,8 = 3,2 (cm)
A H 2 = BH.CH ⇒ AH = B H . C H = 1 , 8 . 3 , 2 = 2,4 (cm)
Xét tứ giác AMHN có:
∠(MAN) = ∠(ANH) = ∠(AMH) = 90 0
⇒ Tứ giác AMHN là hình chữ nhật
⇒ MN = AH = 2,4 (cm)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A , vẽ đường cao AH . Biết AB = 6,5 cm , BH = 2,5 cm, tính độ dài các đoạn thẳng AH ,HC ,BC, AC
cho tam giác ABC cân tại A vẽ đường cao BH CK
a/ cm tam giác BKC đồng dạng tam giác CHB
b/ cm KH//BC
a: Xét ΔKBC vuông tại K và ΔHCB vuông tại H co
BC chung
góc KBC=góc HCB
=>ΔKBC đồng dạng với ΔHCB và ΔKCB=ΔHBC
b: AK+KB=AB
AH+HC=AC
mà HC=KB; AB=AC
nên AK=AH
mà AB=AC
nên KH//BC
Đúng 1
Bình luận (0)
1.cho tam giác ABC vông tại A, đường cao AH. Biết AB=3cm, BC=5cm. Tính AC, AH, BH, CH 2. Cho tam giác ABC vông tại A, đường cao AH. Biết HB=3,6cm, HC=6,4cm. Tính BC,AB,AC,AH
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=5^2-3^2=16\)
hay AC=4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{3^2}{5}=1.8\left(cm\right)\\CH=\dfrac{4^2}{5}=3.2\left(cm\right)\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot5=3\cdot4=12\)
hay AH=2,4cm
Đúng 1
Bình luận (0)
Bài 2:
Ta có: BC=HB+HC
nên BC=3,6+6,4
hay BC=10cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=3.6\cdot10=36\\AC^2=6.4\cdot10=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=6\left(cm\right)\\AC=8\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AH^2=6^2-3.6^2=23.04\)
hay AH=4,8cm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A; đường cao AH ( H thuộc BC ) và phân giác CM ( M thuộc AB ). N là giao điểm AH và CM. Biết BH = 3cm; HC = 27cm. Chứng minh AH2 = BH x HC.