1. a) Cho hình 69b.
- Chứng minh tam giác ABD=tam giác ACD
- So sánh góc DBC và góc DCB
cho tam giác abc cân tại a điểm d nằm trong tam giác sao cho bad=cad
a, CM rằng tam giác abd = tam giác acd
b,so sánh góc dbc và góc dcb
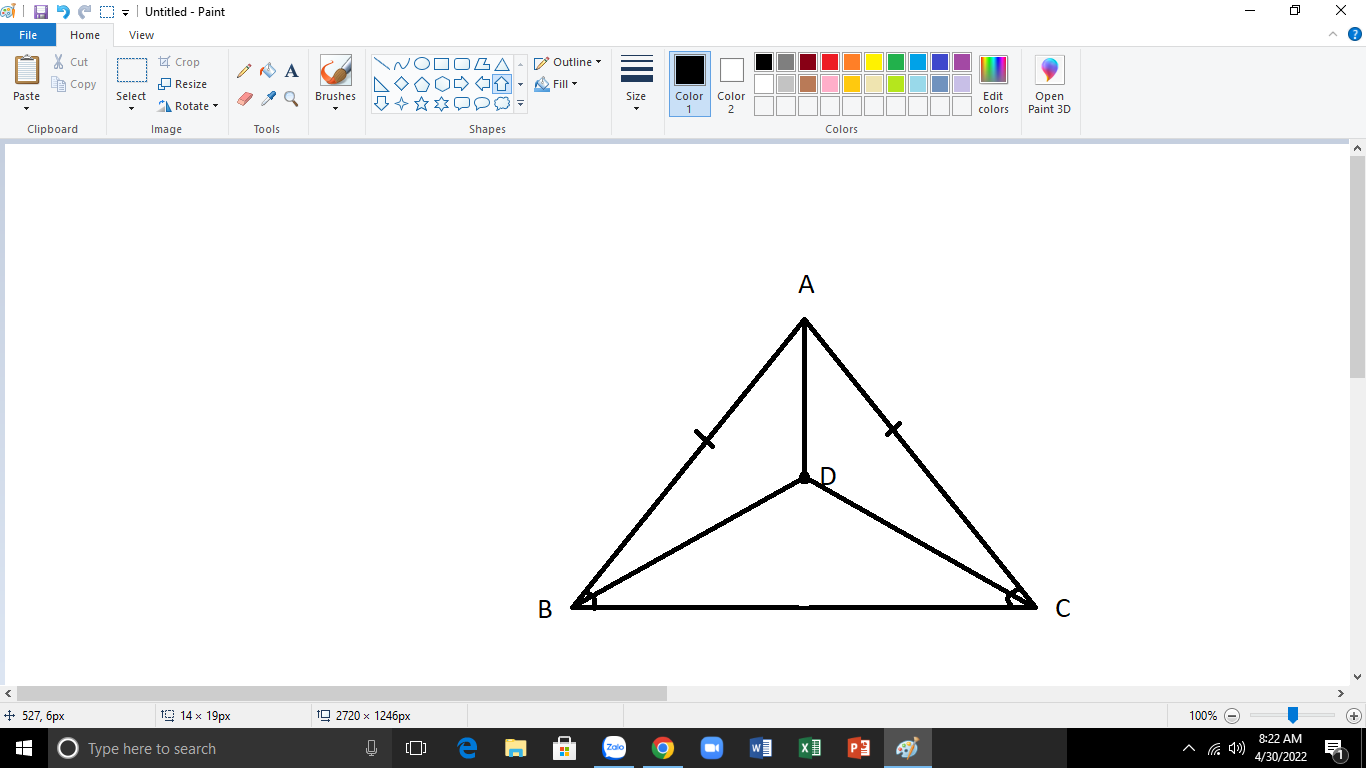
\(\text{a)Xét }\Delta ABD\text{ và }\Delta ACD\text{ có:}\)
\(AB=AC\left(\Delta ABC\text{ cân tại A}\right)\)
\(\widehat{BAD}=\widehat{CAD}\left(gt\right)\)
\(AD\text{ chung}\)
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{ACD}\left(\text{hai góc tương ứng}\right)\)
\(\text{b)Ta có:}\widehat{B}=\widehat{C}\left(\Delta ABC\text{ cân tại A}\right)\)
\(\text{Mà }\widehat{ABD}=\widehat{ACD}\left(cmt\right)\)
\(\Rightarrow\widehat{DBC}=\widehat{DCB}\)
cho tam giác abc cân tại a điểm d nằm trong tam giác sao cho bad=cad
a, CM rằng tam giác abd = tam giác acd
b,so sánh góc dbc và góc dcb
Đây nha:
a. Xét tam giác ABD và tam giác ACD có:
góc BAD = góc BAC (gt)
AD chung
AB = AC (tam giác ABC cân)
=> tam giác ABD = tam giác ACD (cgc)
b. Gọi E là trung điểm của BC
Có: góc BAC = góc BAD + góc CAD mà góc BAD = góc CAD
=> AD là đường phân giác
Lại có: tam giác ABC cân tại A => AD đồng thời là đường trung trực của tam giác ABC
Do đó: DE là đường trung trực cũng là đường phân giác của tam giác BDC.
=> DE vuông với BC tại E; góc BDE = góc CDE
Xét tam giác BDE và tam giác CDE vuông tại E có:
DE chung
góc BDE = góc CDE (cmt)
=> tam giác BDE = tam giác CDE (ch-cgv)
=> góc DBC = góc DCB (2 góc tương ứng)
cho tam giác abc cân tại a. d là điểm nằm trong tam giác sao cho ad là tia phân giác của góc a chứng minh a tam giác abd bằng tam giác acd b góc dbc bằng góc dcb
Cho tam giác ABC cân tại A. Điểm D nằm trong tam giác sao cho BAD^ = CAD^ A) chứng minh tam giác ABC = tam giác ACD B) so sánh DBC^ và DCB^
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó; ΔABD=ΔACD
b: Xét ΔDBC có DB=DC
nên ΔDBC cân tại D
hay \(\widehat{DBC}=\widehat{DCB}\)
Sửa đề chứng minh tam giác ABC = tam giác ACD => △ABD = △ACD
Xét △ABD và △ACD có
AB = AC
AD là cạnh chung
\(\widehat{BAD}=\widehat{CAD}\)
nên △ABD = △ACD (c-g-c)
b)
Ta có:
\(\text{△ABD = △ACD }\)
\(\text{=> DB = DC}\)
\(\text{=> △DBC cân tại D}\)
\(=>\)\(\widehat{DBC}=\widehat{DCB}\)
Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đểu ba cạnh của tam giác ABC
a) Chứng minh: Tam giác ABD= tam giác ACD
b) So sánh DBC và DCB
c) chứng minh: AD đi qua trung điểm M của BC.
d) chứng minh ba điểm A,G,I thẳng hàng
Cho hình 39 :
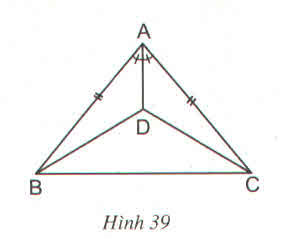
a) Chứng minh \(\Delta ABD=\Delta ACD\)
b) So sánh góc DBC và góc DCB
a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=>
Hướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210

c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
a,
Xét tam giác ABD và tam giác ACD có :
AD là cạnh chung
góc A1 = góc A2
AB=AC
Do đó: tam giác ABD - tam giác ACD ( c-g-c )
b,
từ tam giác ABD= tam giác ACD (c-g-c)
suy ra đc BD=BC
suy ra dc tam giác DBC là tam giác cân
suy ra dc góc DBC=góc DCB
Cho hai tam giác ABC và DBC có chung cạnh BC, hai đỉnh A và D nằm trong hia nửa mặt phẳng đối nhau bờ là đường thẳng BC, biết rằng cạnh BC là tic phân giác của góc ABD và góc ACD:
a) So sánh các cạnh của hai tam giác ABC và DBC
b) Nối A và D với một điểm E thuộc cạnh BC, so sánh AE và DE. Tìm tia phân giác của góc AED
c) Nối AD, gọi F là giao điểm của AD và BC. Chứng minh F là trung điểm của AD và AF vuông góc với BC.-
Cho hai tam giác ABC và DBC có chung cạnh BC, hai đỉnh A và D nằm trong hia nửa mặt phẳng đối nhau bờ là đường thẳng BC, biết rằng cạnh BC là tic phân giác của góc ABD và góc ACD:
a) So sánh các cạnh của hai tam giác ABC và DBC
b) Nối A và D với một điểm E thuộc cạnh BC, so sánh AE và DE. Tìm tia phân giác của góc AED
c) Nối AD, gọi F là giao điểm của AD và BC. Chứng minh F là trung điểm của AD và AF vuông góc với BC.
1.Cho hình thanh ABCD (AB//CD) có góc DAB = góc DBC. Chứng minh tam giac ABD ~ tam giac BDC
2.Cho tam giác ABC, D thuộc cạnh AC sao cho góc ABD = góc C. Chứng minh tam giac ABC~ tam giác ADB