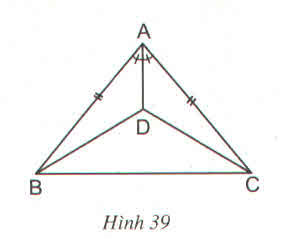
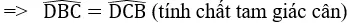a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=>
Hướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210

c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
a,
Xét tam giác ABD và tam giác ACD có :
AD là cạnh chung
góc A1 = góc A2
AB=AC
Do đó: tam giác ABD - tam giác ACD ( c-g-c )
b,
từ tam giác ABD= tam giác ACD (c-g-c)
suy ra đc BD=BC
suy ra dc tam giác DBC là tam giác cân
suy ra dc góc DBC=góc DCB
a) Căn cứ vào các kí hiệu đã cho trên hình của bài 39 ta có:
ΔABD và ΔACD có:
AB = AC
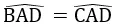
AD là cạnh chung
⇒ ΔABD = ΔACD (c.g.c)
b) Vì ΔABD = ΔACD (chứng minh câu a)
⇒ BD = CD (hai cạnh tương ứng)
⇒ ΔBCD cân tại D